— Tutorial nº 121 —
Correas de Transmisión
Cálculo y Diseño
Índice de contenidos:
1- Introducción
1.1- Generalidades
1.2- Clasificación
2- Correas trapezoidales
2.1- Generalidades
2.2- Constitución
2.3- Longitud primitiva
2.4- Identificación
3- Correas dentadas o síncronas
3.1- Generalidades
3.2- Constitución
3.3- Series normalizadas
4- Poleas
4.1- Generalidades
4.2- Diámetro mínimo
4.3- Ajuste de la distancia entre poleas
4.4- Operación de tensado
5- Procedimiento de cálculo
5.1- Generalidades
5.2- Potencia transmitida
5.3- Selección del tipo de correa
5.4- Relación de transmisión
5.5- Diámetros de poleas
5.6- Distancia entre ejes
5.7- Longitud de la correa
5.8- Arco de contacto
5.9- Velocidad lineal de la correa
5.10- Prestación base de la correa
5.11- Potencia efectiva por correa
5.12- Cálculo del número de correas
ANEXOS:
A.1- Ejemplo de cálculo
A.2- Catálogo de correas industriales Dunlop
DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Generalidades
Las correas son elementos de transmisión de potencia, de constitución flexible, que se acoplan sobre poleas que son solidarias a ejes con el objeto de transmitir pares de giro.
Su naturaleza flexible va a permitir que su fabricación se realice con una cierta incertidumbre mecánica que puede ser asumida, posteriormente, en su montaje.
La correa de transmisión trabaja por rozamiento con la polea sobre la que va montada. Este hecho, junto a su naturaleza flexible, confiere a las correas una función de "fusibles" dentro de las transmisiones, dado que se comportan como amortiguador, reduciendo el efecto de las vibraciones que puedan transmitirse entre los ejes de la transmisión.
En general, el empleo de correas en las transmisiones resulta una opción más barata, pero como contrapartida, este tipo de elementos no pueden garantizar una relación de transmisión siempre constante entre ejes, dado que pueden originarse pequeños deslizamiento de la correa sobre la canaladura de la polea, debido, por ejemplo, a que el tensado inicial no se ha hecho correctamente, o en todo caso, producido por el desgaste con las horas de funcionamiento.
1.2- Clasificación
Las correas de transmisión se clasifican en:
• Correas planas: actualmente ya en desuso y sustituidas gradualmente por las trapezoidales, se utilizaban sobretodo en aquellas transmisiones donde no se requerían grandes prestaciones, esto es, que no se transmiten grandes pares ni la velocidad lineal que alcanza la correa es elevada (< 5 m/s). También pueden emplearse cuando la distancia entre ejes de poleas es elevada. Las correas planas se dividen a su vez en correas "sin fin", también llamadas correas continuas, y correas abiertas, que se denominan así porque se suministran abiertas para su montaje y posteriormente son cerradas mediante grapas o pegamento industrial.
• Correas trapezoidales o de sección en "V": las correas en "V" permiten transmitir pares de fuerzas más elevados, y una velocidad lineal de la correa más alta, que puede alcanzar sin problemas hasta los 30 m/s.
• Correas dentadas o síncronas (timing belts): tienen aplicación sobretodo en aquellas transmisiones compactas y que se requieren trasmitir alta potencia. En este caso se deben emplear poleas de pequeño diámetro, y las correas dentadas ofrecen mayor flexibilidad y mejor adaptabilidad al dentado de la polea. Por otro lado, también permiten ofrecer una relación de transmisión constante entre los ejes que se acoplan.
2- Correas trapezoidales
2.1- Generalidades
Las correas trapezoidales o correas en "V" trabajan a partir del contacto que se establece entre los flancos laterales de la correa y las paredes del canal de la polea.
Según las normas ISO las correas trapezoidales se dividen en dos grandes grupos: las correas de secciones con los perfiles clásicos Z, A, B, C, D y E, y las correas estrechas de secciones SPZ, SPA, SPB Y SPC. En la figura adjunta se representa esquemáticamente una sección tipo de correa trapezoidal o correa en "V":
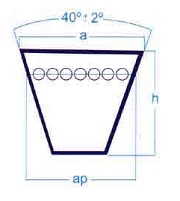
Figura 1. Esquema de una correa trapezoidal
donde,
a es el ancho de la cara superior de la correa;
h es la altura o espesor de la correa;
ap es el denominado ancho primitivo de la correa.
En la siguiente tabla se muestran los valores de los parámetros anteriores según el perfil de correa:
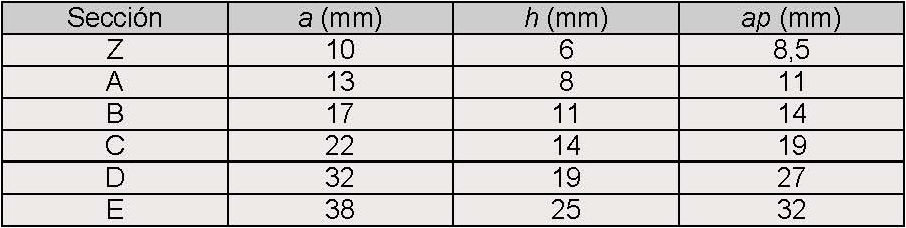
Tabla 1. Perfiles normalizados para correa trapezoidal
Las correas trapezoidales o en "V" trabajan en condiciones óptimas cuando lo hacen a velocidades lineales dentro del rango de los 20-22 m/s. Las correas en "V" no deben trabajar a velocidades superiores de los 30 m/s, dado que la elevada fuerza centrífuga que se genera terminaría sacando la correa de la ranura de la polea. Por otro lado, si funcionasen a velocidades más baja también necesitarían un proceso de equilibrado estático para conseguir un trabajo más óptimo.
2.2- Constitución
La siguiente figura muestra una sección tipo de una correa trapezoidal, así como de las partes principales que la compone:

Figura 2. Elementos de una correa trapezoidal
donde,
1, es el núcleo;
2, tensores o fibras resistentes;
3, recubrimiento.
a) Núcleo
La parte del núcleo está constituido de una mezcla de cauchos especiales que le proporcionan a la correa una alta resistencia mecánica y una gran capacidad de flexión para un rango de temperatura de trabajo amplio, de entre -10 ºC y 90 ºC.
No obstante, esta parte de la correa es sensible al contacto con aceites, grasas, u otros agentes químicos, por lo que se recomienda evitar un prolongado contacto de la correa con estas sustancias.
b) Tensores o fibras resistentes
Para mejorar la resistencia a tracción de las correas y evitar que se alarguen o deformen se incluyen estos elementos tensores, generalmente hechos de fibras sintéticas (poliéster o fibra de vidrio) que ofrecen una gran resistencia a la fatiga. Debido a que las correas se ven sometidas a continuos y repetitivos ciclos de carga y descarga, es el agotamiento por fatiga lo que condiciona realmente la vida útil de las correas, de ahí la importancia de estos elementos.
c) Recubrimiento
Es una envolvente textil que recubre y protege a los demás elementos de la correa. Consiste en una tela mixta de algodón-poliéster que ofrece una excelente resistencia a la abrasión, además de proporcionar un elevado coeficiente de rozamiento o fricción con la superficie de la polea.
Un elevado coeficiente de rozamiento entre correa y polea es importante porque así se evita cualquier riesgo de deslizamiento, lográndose una mejor y óptima transmisión de potencia.
Además, el material que constituye el recubrimiento debe ofrecer una buena resistencia a los agentes de la intemperie que puedan dañar la correa, como aceites, polvo, a las altas temperaturas y radiación.
Otro factor importante es la electricidad estática que se genera durante el funcionamiento de una correa. La acumulación de electricidad estática se produce, fundamentalmente, por el continuo rozamiento de las partes de la correa con las partículas del aire. La tela del recubrimiento debe ofrecer una buena conductividad eléctrica que ayude a evacuar esta acumulación de electricidad estática, porque de lo contrario podría dar lugar a la generación de chispas con el consiguiente peligro de incendio.
2.3- Longitud primitiva
La longitud o desarrollo lineal de una correa se mide montada sobre poleas y convenientemente tensada. En esta situación el desarrollo de una correa variará en función de la línea de referencia de la sección que se tome para realizar la medición. Así, se denomina longitud primitiva de la correa (Lp) a la que resulta de realizar la medición de su longitud a la altura del ancho primitivo (ap) de la sección.
Para efectuar correctamente la medición de la longitud primitiva de la correa, ésta debe estar, como ya se ha dicho, convenientemente tensada. Para poder aplicar el tensado a la correa, las dos poleas sobre las que se monte la correa deben ser una fija y la otra desplazable con el objeto de poder aplicarle a esta última la carga (Q) de tensado.
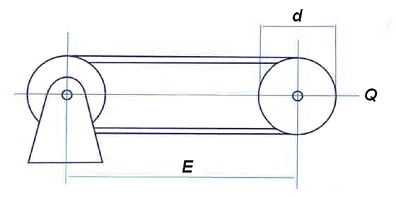
Figura 3. Esquema de montaje de una transmisión por correa
La carga (Q) de tensado a aplicar será función de la sección de la correa que se trate, su desarrollo primitivo y del diámetro de poleas, según se indica en la siguiente tabla:
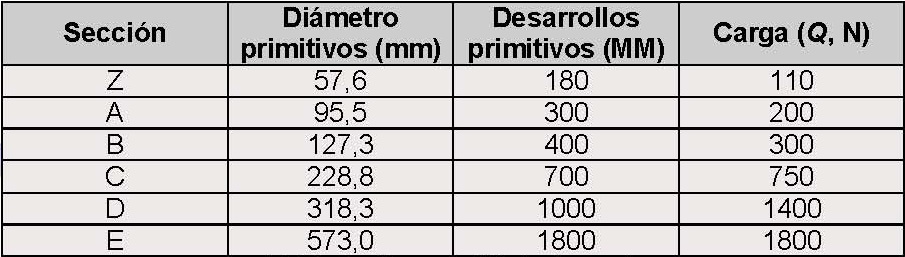
Tabla 2. Cargas (Q) de tensado
La distancia entre ejes de poleas (E) se mide con la correa ya montada y tensada. Para que la medición sea correcta se debe hacer girar las poleas cuatro o cinco vueltas a fin que la correa encaje bien en la ranura.
La longitud primitiva (Lp) de la correa para este caso concreto, donde los diámetros de las poleas son iguales y el ángulo de contacto igual a 180º, resulta inmediato aplicando la siguiente expresión:
Lp = 2 · E + Π · d
donde,
E es la distancia entre ejes de las poleas, en mm;
d es el diámetro primitivo de las poleas, en mm;
Lp es la longitud primitiva de la correa, en mm.
Como ya se dijo al principio de este apartado, la longitud o desarrollo de la correa variará en función de qué línea de referencia de la sección se tome. Así, si se toma la cara externa de la sección de la correa como referencia, resultará una longitud nominal mayor que la longitud primitiva, y por el contrario, si se toma la cara interna, entonces la longitud nominal obtenida será menor que la longitud primitiva. Es decir, que
Desarrollo externo = Longitud primitiva nominal (Lp) + C1;
Desarrollo interno = Longitud primitiva nominal (Lp) - C2;
Los coeficientes C1 y C2 que hay que sumar o restar a la longitud primitiva para obtener los desarrollos exteriores o interiores de la correa, se adjuntan en la siguiente tabla en función del tipo de sección:
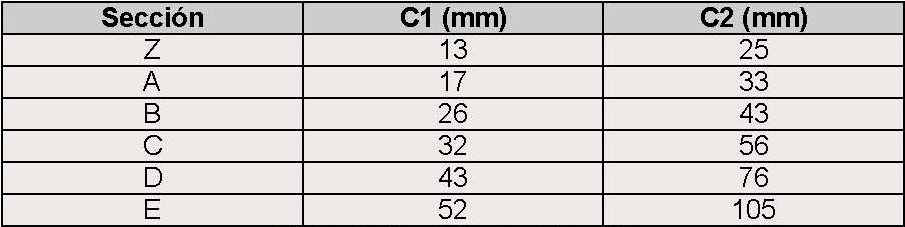
Tabla 3. Coeficientes C1 y C2
2.4- Identificación
Las correas trapezoidales se identifican por sus dimensiones físicas. Así, para proceder a su identificación se coloca en primer lugar una letra que indica la sección de la correa, seguido por un número que expresa la longitud nominal de la correa.

Figura 4. Identificación de correa trapezoidal
3- Correas dentadas o síncronas
3.1- Generalidades
Cuando se requiere transmitir elevados régimen de potencia, en transmisiones que son compactas, lo cual va a suponer el empleo de poleas de reducido diámetro y elevadas velocidades de giro, lo normal es utilizar poleas dentadas o síncronas.
Las poleas dentadas garantizan una relación de transmisión constante al disminuir el riesgo de deslizamiento sobre la polea.
Por otro lado, la incorporación del dentado a la correa le confiere de una mayor flexibilidad longitudinal lo que le permite poder adaptarse a poleas de diámetros más pequeños.
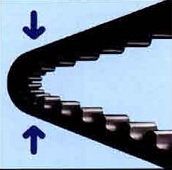
Figura 5. Elevada flexibilidad en correas dentadas
En definitiva, para aplicaciones donde se requiera exactitud en la relación de transmisión, unido a exigencias de altas velocidades de giro, o que por consideraciones de diseño no sea posible el engrase o lubricación de los componentes de la transmisión, entonces el empleo de correas dentadas o síncronas es la mejor opción.
Por último indicar que los requerimientos de un tensado inicial de la correa, como ocurre con las correas trapezoidales, no son tan exigentes para el caso de las dentadas.
3.2- Constitución
La siguiente figura muestra la sección tipo de una correa síncrona, así como de las partes principales que la compone:

Figura 6. Elementos de una correa dentada
donde,
1, es el núcleo de la correa,
2, indica las fibras de refuerzo,
3, es el recubrimiento exterior de la correa.
a) Núcleo
El núcleo de este tipo de correa está compuesto de un caucho de altas prestaciones reforzado con fibras sintéticas orientadas de tal modo que le proporciona una gran rigidez en sentido transversal.
De igual manera, el cojín que es la parte del núcleo que queda por encima de los tensores de refuerzo consta de fibras sintéticas orientadas que le proporcionan del mismo modo una elevada rigidez transversal.

Figura 7. Elevada rigidez transversal
En el caso de las correas síncronas, el núcleo de los dientes ofrece una gran rigidez y es la parte de la correa que absorbe la mayor parte de los esfuerzos, como ya se vio en una figura anterior, descargando de tensiones el resto de la correa.
Por otro lado, en las correas síncronas se distinguen dos tipos de perfiles de dientes normalizados: trapezoidal y curvilíneos.
La gran ventaja conseguida con los perfiles curvilíneos es que la zona de alta concentración de tensiones se sitúa en el centro del diente, frente a las correas dentadas de perfil trapezoidal, donde los mayores niveles de tensión se concentran en la esquina de la base del diente del lado que arrastra la polea, reduciendo su duración.
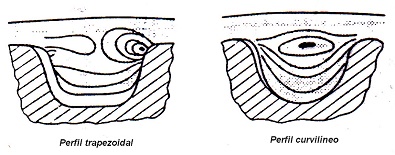
Figura 8. Distribución de tensiones en correas dentadas
En la figura anterior se aprecia que el perfil curvilíneo se adapta mejor a la dentadura de la polea y redistribuye mejor las tensiones.
b) Tensores o fibras resistentes
Fibras sintéticas, generalmente fibra de vidrio, de alta tenacidad y elevada estabilidad dimensional que evita la deformación longitudinal de la correa.
c) Recubrimiento
Envolvente textil que recubre a la correa y proporciona protección de los agentes nocivos exteriores.
De igual forma que para las correas trapezoidales, el recubrimiento debe tener buenas propiedades de conductividad para eliminar la electricidad estática que se vaya acumulando, así como de comportarse adecuadamente para un amplio rango de temperaturas de trabajo (generalmente, de -10 ºC a 90 ºC), y de ofrecer buena resistencia a los aceites.
3.3- Series normalizadas
Las correas dentadas están normalizadas según la forma de los dientes (curvilíneo o trapezoidal) y el paso entre ellos.
A continuación en la siguiente tabla se indican las distintas series normalizadas y dimensiones para las correas dentadas con perfil de dientes trapezoidal:
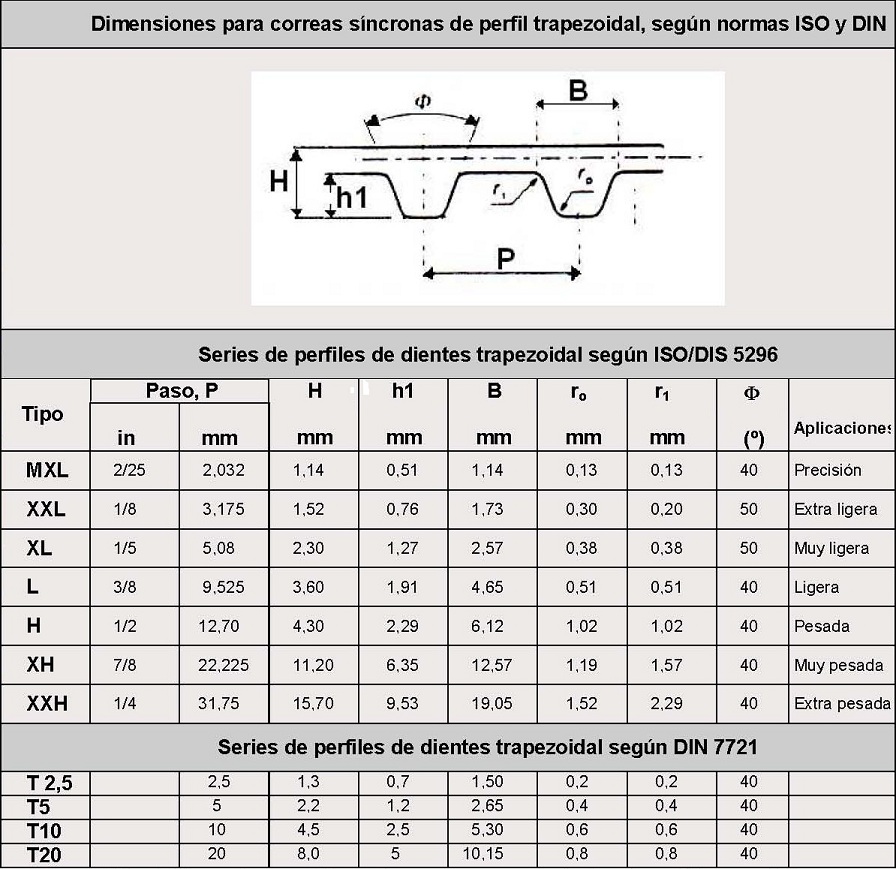
Tabla 4. Dimensiones y tolerancias para correas dentadas de perfil trapezoidal
En la siguiente tabla se muestran las series normalizadas y dimensiones de correas dentadas con perfil de diente curvilíneo HTD:
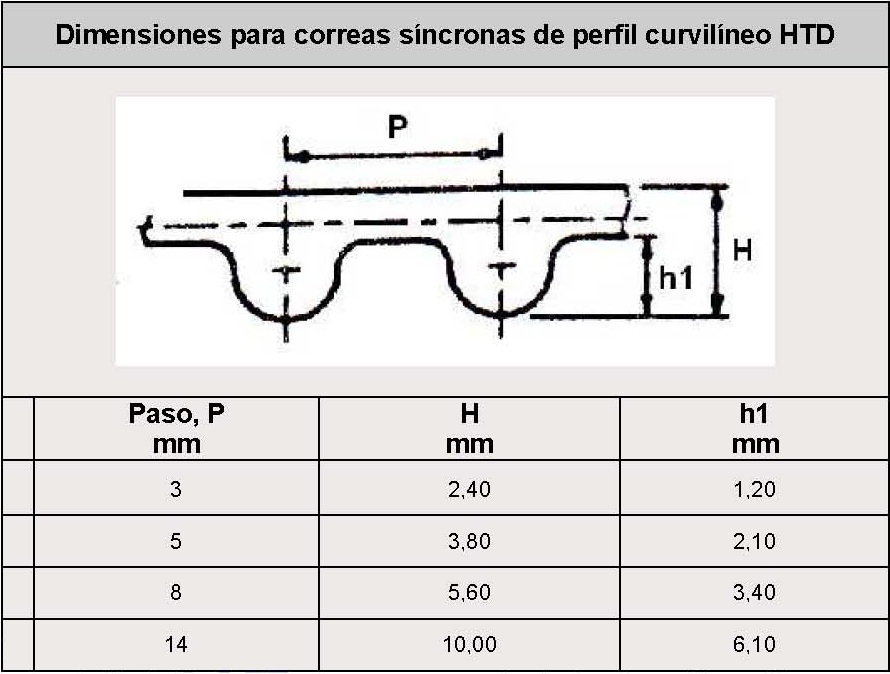
Tabla 5. Dimensiones para correas dentadas de perfil curvilíneo
A continuación se incluye una serie de datos técnicos que son necesarios para poder seleccionar y diseñar de forma adecuada la correa síncrona que sea válida a los requerimientos para cada situación de trabajo.
Así, mediante las siguientes gráficas se puede seleccionar el tipo de correa más adecuada según la magnitud de la potencia a transmitir (Pc) y la velocidad de giro de la transmisión (N):
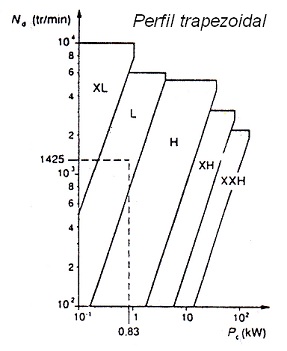
Figura 9. Ábaco para selección de correas dentadas de perfil trapezoidal
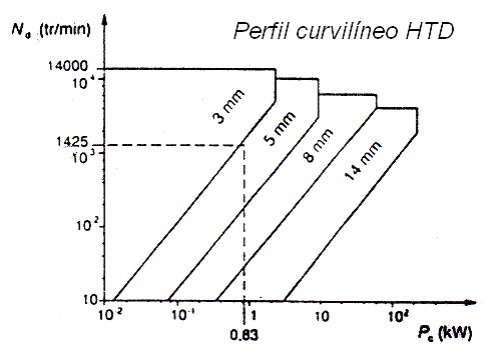
Figura 10. Ábaco para selección de correas dentadas de perfil curvilíneo HTD
En la siguiente tabla se indica el esfuerzo máximo admisible, peso por unidad de longitud y anchuras de base normalizadas para correas síncronas, según datos del fabricante:
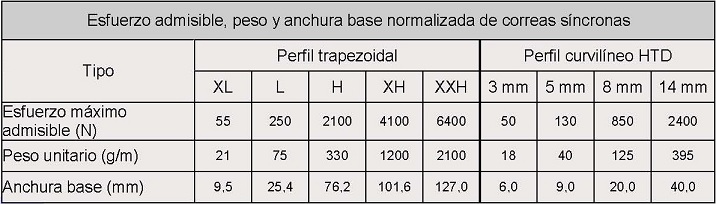
Tabla 6. Datos de esfuerzo admisible, peso y anchura de correas síncronas
Por último, en la siguiente tabla se muestran unas consignas o recomendaciones de uso para correas síncronas:
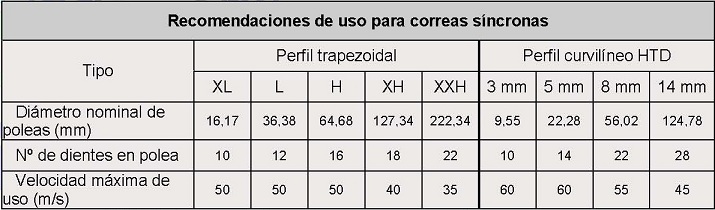
Tabla 7. Recomendaciones de uso para correas síncronas
4- Poleas
4.1- Generalidades
La colocación de la correa de manera correcta en el canal o ranura de la polea influye considerablemente en el rendimiento de la transmisión y en la vida útil de la correa.
Para conseguir una buena colocación de la correa en la ranura de las poleas es condición imprescindible un perfecto alineamiento entre poleas. Para ello es necesario que los ejes del motor sean paralelos y que la correa trabaje perpendicularmente a dichos ejes.
Es síntoma de que existe un mal alineamiento entre poleas cuando uno de los flancos de la correa está más desgastado que el otro, o que un lado del canal aparece más pulido que el otro. Un ruido constante de la transmisión o un calentamiento excesivo de los rodamientos son también síntomas de un mal alineamiento entra poleas.
Por otro lado, como ya se ha indicado, la correa en "V" trabaja por rozamiento entre los flancos laterales de la correa y las paredes del canal de la polea. Es por ello muy importante que los flancos de la polea se presenten perfectamente lisos y limpios. La presencia de suciedad o de partículas de polvo en la polea es muy perjudicial al convertirse en abrasivos que terminan desgastando a la superficie de la correa.
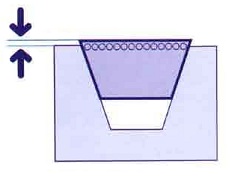
Figura 11. Colocación de la correa en el canal de la polea
La posición correcta de la correa será aquella en la que su base mayor quede por encima de la polea, lo cual va a asegurar un contacto continuo entre la ranura y los flancos de la correa. En ningún caso la correa debe tocar el fondo del canal de la polea, dado que de producirse, la correa empezaría a patinar, y esto provocaría su desgaste inmediato.
Por ello, en poleas con canales muy gastados deben ser reemplazadas de inmediato, dado que las correas pueden tocar el fondo del canal lo que terminaría "quemando" la correa y perdería su capacidad de transmitir la potencia.
4.2- Diámetro mínimo
La elección del diámetro correcto de las poleas es sumamente importante, dado que un diámetro excesivamente pequeño para una sección de correa determinada significaría una flexión excesiva de ésta, lo que terminaría reduciendo su vida útil. Como norma general, al aumentar el diámetro de la polea aumentará la vida útil de la correa.
A continuación se incluye una tabla donde se indica, según la norma BS 3790, los diámetros de polea válidos para cada sección de correa. Diámetros inferiores a los indicados en la siguiente tabla, según la sección de la correa, no deben emplearse:
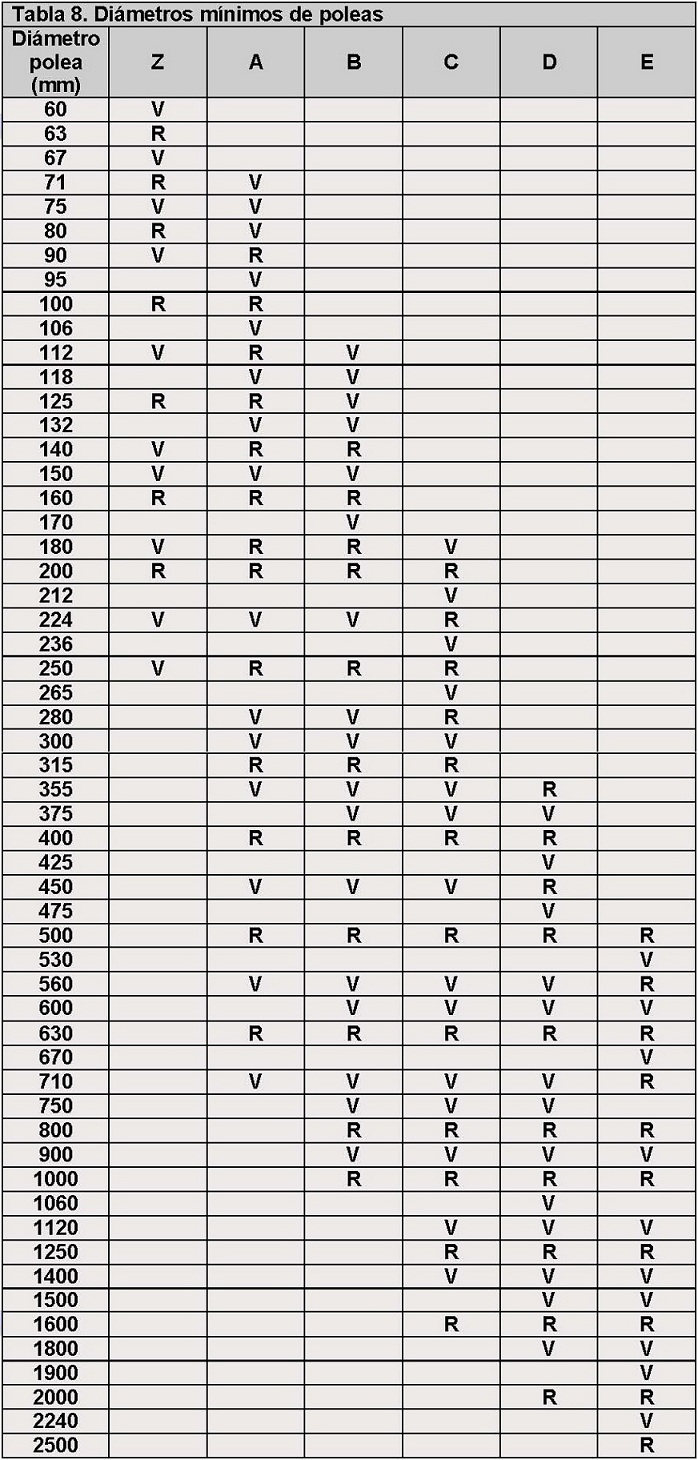
Tabla 8. Diámetros mínimos de poleas
siendo,
V diámetro válido de polea;
R diámetro de polea especialmente recomendado.
4.3- Ajuste de la distancia entre poleas
Toda transmisión por correas flexibles debe ofrecer la posibilidad de ajustar la distancia entre centros de poleas, es decir, de poder variar la distancia que separa los ejes de giro de las distintas poleas que permita realizar las siguientes operaciones:
- hacer posible el montaje inicial de la correa sin forzarla;
- una vez montada, poder realizar la operación de tensado inicial;
- durante la vida útil de la correa, para poder compensar el asentamiento de la correa o su alargamiento que se produce por el uso.
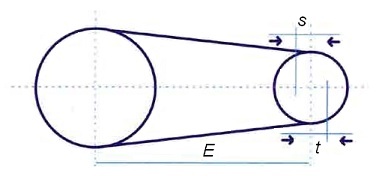
Figura 12. Ajuste de la distancia entre poleas
En la siguiente tabla se indica la variación mínima de la distancia entre ejes de poleas necesario para la instalación y tensado de las correas:
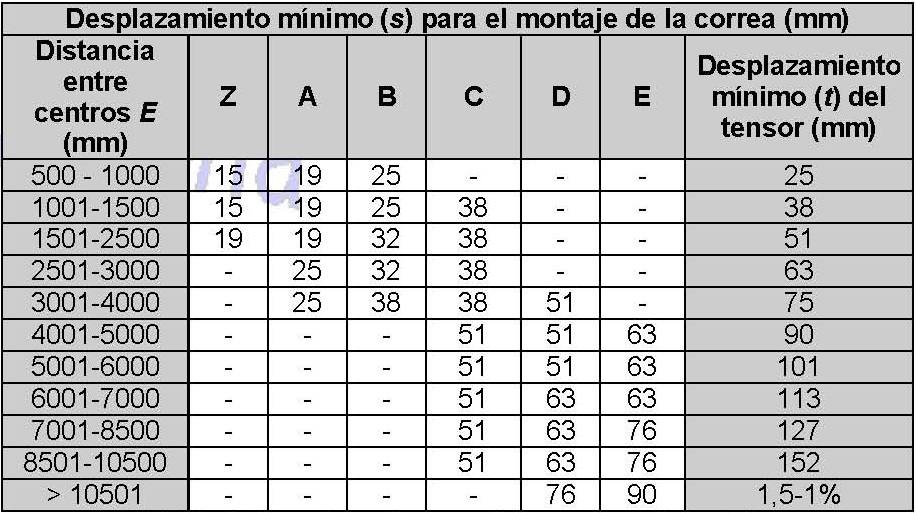
Tabla 9. Desplazamientos mínimos para el montaje
4.4- Operación de tensado
La operación de tensado de las correas, necesaria y previa a la puesta en servicio de la transmisión, se llevará a cabo una vez asegurada la correcta alineación entre poleas.
En primer lugar, una vez montada la correa, se le da a ésta un pequeño tense por el lado de la transmisión. El ramal tenso de una correa es aquel que se dirige hacia la polea motriz. Una vez dada esta pequeña tensión se le daría varias vueltas manualmente a la transmisión para asegurarse una mejor colocación de la correa en el canal.
Posteriormente se debe ajustar los centros de las poleas hasta aumentar algo más la tensión de la correa, conectando posteriormente el motor de accionamiento durante varias vueltas con el fin de permitir a las correas asentarse correctamente en las ranuras de las poleas.
Se para de nuevo el motor, y a continuación se ajusta la distancia entre centros hasta alcanzar la tensión correcta.
Por último quedaría comprobar que la tensión dada es la correcta y recomendada por el fabricante. Para la medición de la tensión que tiene una correa se procederá como a continuación se expone.
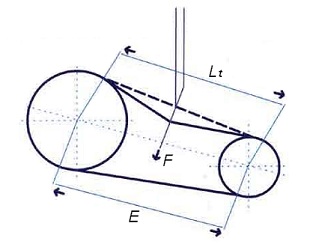
Figura 13. Medida del tensado
Como muestra la figura anterior, la medida del tensado consiste en esencia en someter a la correa a una determinada deflexión mediante la aplicación de una fuerza F perpendicular al tramo medio (Lt) de la correa, mediante el uso de un tensor resorte, dispositivo que permite medir la magnitud de la fuerza aplicada. La longitud del tramo (Lt) puede ser calculada también por la siguiente expresión:

siendo,
E la distancia entre ejes de poleas;
d el diámetro de la polea menor;
D el diámetro de la polea mayor.
La deflexión a conseguir es de 0,02 mm si la longitud del tramo (Lt) es menor a 500 mm, o de 0,01 mm si excede de 500 mm. A continuación se anota el valor de la fuerza F aplicada para conseguir estas deflexiones y se compara con los valores dados en la tabla siguiente suministrada por los fabricantes de correas.
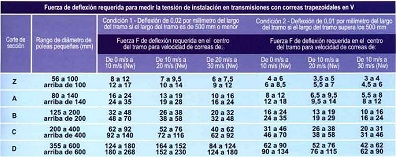
Tabla 10. Fuerza de deflexión para medir el tensado de correas en "V"
Una fuerza F medida por debajo del mínimo indicado en la tabla anterior significaría que le falta tensado a la correa, y por encima que la correa estaría trabajando en sobre tensión.
No obstante, cuando se instalan correas nuevas, éstas deben tensarse a su valor máximo permitido, dado que tras las primeras horas de funcionamiento una correa nueva tienden a perder rápidamente algo de la tensión inicial por su deformación hasta que alcanza la estabilidad.
5- Procedimiento de cálculo
5.1- Generalidades
Todo fabricante que comercialice correas de transmisión dispone de catálogos con las especificaciones técnicas de sus correas que es accesible al público en general.
En dichas especificaciones técnicas se incluyen, para cada sección nominal, la potencia que puede transmitir cada correa, en función del diámetro y las r.p.m. a que gire la polea más pequeña, ya que ésta es la que va a condicionar la resistencia por fatiga a flexión de la correa.
No obstante los valores de estas tablas son teóricos, y están calculados suponiendo unas hipótesis de cargas constantes y un arco de contacto de la correa sobre la polea de 180º.
Evidentemente, la realidad en cada caso será distinta y habrá que ajustarse a las condiciones específicas de trabajo a la que se someta a la correa. Es por ello que es necesario hacer uso de unos coeficientes de corrección que tengan en cuenta la realidad en el diseño y las condiciones de trabajo de cada correa.
En los siguientes apartados se mostrarán cómo calcular dichos coeficientes correctores, necesarios para realizar correctamente el cálculo y diseño de una correa de transmisión de potencia.
5.2- Potencia transmitida
En primer lugar habrá que calcular la potencia de diseño o total de la potencia transmitida sobre la que se diseñará la correa. La potencia que desarrolla el motor conductor (P) es el punto de partida, pero a este valor habrá que afectarlo de un coeficiente corrector en función de diversos factores como son:
• Tipo de motor conductor que se utilice para accionar la transmisión
• Tipo de máquina conducida que se vaya a accionar
• Horas de servicio por día.
De esta manera la potencia corregida (Pc) o total de la potencia transmitida, que es la que habrá que utilizar en el diseño, vendrá dada por la siguiente expresión:
Pc = P · K, donde
Pc es la potencia corregida;
P es la potencia transmitida del motor conductor;
K es el factor de corrección de la potencia de acuerdo a la siguiente tabla:
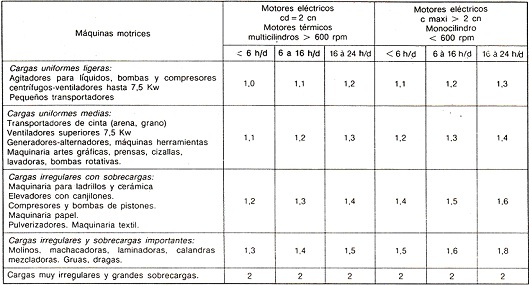
Tabla 11. Factor de servicio, K
A la tabla anterior, cuando sea necesario el uso de poleas tensoras, habrá que adicionar al coeficiente de corrección anterior los valores siguientes en función de la posición de la polea tensora:
- sobre el ramal flojo interior: ---
- sobre el ramal flojo exterior: +0,1
- sobre el ramal tenso interior: +0,1
- sobre el ramal tenso exterior: +0,2
En ocasiones, en lugar de la potencia del motor de accionamiento (P) lo que se dispone es su par motor (T). En este caso la potencia (P) que transmite se calcula de la siguiente manera:
donde P resulta la potencia transmitida en kW, n son las revoluciones por minuto (rpm) y T es el par motor en kg fuerza · metro.
5.3- Selección del tipo de correa
Cada fabricante dispone de gráficas donde se muestra el tipo de correa adecuada para trabajar en función de la potencia a transmitir y de las revoluciones de giro de la polea menor.
Se adjunta una gráfica tipo de un fabricante de correas de transmisión donde se puede seleccionar la sección correcta de la correa:
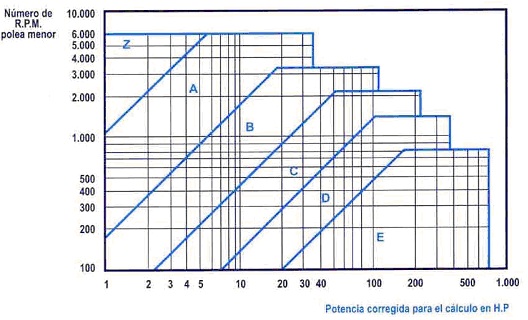
Figura 14. Selección de la sección de correa
5.4- Relación de transmisión
La relación de transmisión se calcula de acuerdo a la siguiente expresión:
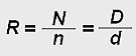
donde,
R es la relación de transmisión;
N son las revoluciones por minuto (rpm) de la polea menor;
n son las revoluciones por minuto (rpm) de la polea mayor;
D es el diámetro de la polea mayor;
d es el diámetro de la polea menor.
5.5- Diámetros de poleas
Generalmente se parte del conocimiento del diámetro de alguna de las poleas, de la mayor o de la menor.
Así, si se parte del diámetro de la polea menor (d), el diámetro de la otra polea, la mayor (D), se obtendría a partir de la relación de transmisión (R).
D = R · d
Si por el contrario, se conoce el diámetro de la polea mayor (D), el de la menor (d) se calcula de igual manera:
d = D / R
Por último, habría que comprobar que el diámetro de la polea menor se elige siempre mayor al mínimo requerido para cada sección, según se indica en la Tabla 8 Diámetros mínimos de poleas del apartado 4.2 de este tutorial.
5.6- Distancia entre ejes
La distancia entre ejes (E) de las poleas suele estar establecida en la transmisión que debe calcularse. No obstante, puede que en algunos casos este dato no esté decidido, quedando a mejor criterio calcular esta distancia.
De acuerdo a la experiencia de las empresas fabricantes, y con el objetivo de optimizar el rendimiento de la transmisión, la distancia entre ejes de poleas (E) mínima se puede obtener a partir de las siguientes expresiones:
• Si la relación de transmisión R está comprendida entre 1 y 3:
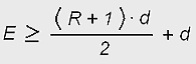
• Si R ≥ 3:
Para este caso bastaría que se cumpliese que E ≥ D
siendo,
E la distancia entre ejes de poleas;
R la relación de transmisión;
d el diámetro de la polea menor;
D el diámetro de la polea mayor.
5.7- Longitud de la correa
La longitud primitiva de la correa (Lp) de una transmisión se calcula directamente a partir de la siguiente expresión:
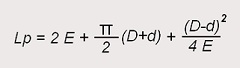
donde,
E es la distancia entre ejes de poleas;
d es el diámetro de la polea menor;
D es el diámetro de la polea mayor;
Π es el número pi (3,14159265)
La expresión anterior calcula el valor exacto para la longitud de la correa. No obstante, las casas comerciales fabrican una serie normalizada de longitudes primitivas nominales para cada sección de correa, que seguramente no coincidirán con la longitud calculada mediante la expresión anterior. Por ello, de esta lista habrá que elegir, para el tipo de correa que se trate, la longitud más próxima al valor calculado.
>> Acceder a la lista de longitudes nominales de correas trapezoidales
Posteriormente, habrá que determinar el factor de corrección del largo de la correa (Fcl). Ello es así porque en las tablas de correas de cualquier fabricante, las prestaciones que en ellas aparecen están confeccionadas para un desarrollo base de la correa. Como en el cálculo que se realice se obtendrá una longitud de correa distinta al desarrollo base con que se han confeccionado las tablas, habrá que afectarles con un coeficiente corrector de longitud (Fcl)
Así, si la longitud obtenida es mayor a la longitud base, habrá que afectarle con un coeficiente corrector mayor a la unidad (Fcl > 1). Esto es así porque al ser la frecuencia con que flexiona una correa inversamente proporcional a su longitud, es decir, a mayor longitud de correa implica menor número de flexiones de cada sección, y por tanto mayor duración, por lo que se estaría del lado de la seguridad y por tanto, el Fcl deberá ser mayor a la unidad (Fcl > 1).
Por el contrario, si la longitud calculada es inferior al desarrollo estándar del fabricante, la prestación será inferior a la indicada en las tablas, y por lo tanto habrá que aplicar un coeficiente corrector menor a 1 (Fcl < 1).
>> Acceder a la Tabla del Factor de corrección por longitud (Fcl)
5.8- Arco de contacto
La polea determinante en el diseño y en la duración de la vida útil de la correa será la de menor diámetro. Por ello, es necesario conocer el ángulo de contacto sobre esta polea.
La determinación del ángulo de contacto (A) de la correa sobre la polea menor se realiza aplicando la siguiente expresión:

donde,
A es el ángulo de contacto sobre la polea menor, en º
E es la distancia entre ejes de poleas;
d es el diámetro de la polea menor;
D es el diámetro de la polea mayor.
Al igual que en el caso anterior, el diseño óptimo de la correa se ha realizado para un ángulo de contacto sobre la polea de 180º. Como en general el ángulo de contacto sobre la polea menor será inferior a 180º, la prestación de la correa no será la óptima, y por tanto habrá que afectarla por un coeficiente corrector del arco de contacto (FcA)
>> Acceder a la Tabla del Factor de corrección del arco de contacto (FcA)
5.9- Velocidad lineal de la correa
Para el cálculo de la velocidad lineal de la correa se emplea la siguiente expresión,
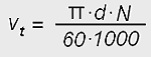
donde,
vt es la velocidad lineal o tangencial de la correa, en m/s;
d es el diámetro de la polea menor, en mm;
N son las revoluciones por minuto (r.p.m.) de la polea menor;
Π es el número pi (3,14159265)
Como ya se ha indicado en algún apartado anterior, la velocidad lineal de una correa trapezoidal no debe sobrepasar los 30 m/s, dado que a partir de esta velocidad las fuerzas centrífugas son de una magnitud tal que podría desencajar la correa de la ranura de la polea. Si se necesitasen velocidades superiores a los 30 m/s se deberá utilizar poleas especiales que eviten este inconveniente.
5.10- Prestación base de la correa
La prestación base o potencia base (Pb) que puede transmitir una correa, según su perfil, están tabuladas en las tablas de cualquier fabricante de correas. Como ya se ha indicado, estas prestaciones están indicadas para un ángulo de contacto de 180º.
En dichas tablas, para acceder a la información de la potencia base de la correa, habrá que entrar con las revoluciones por minuto (rpm) y diámetro de la polea menor.
Se adjunta tablas tipos donde se indican las prestaciones base de las correas trapezoidales para los perfiles clásicos Z, A, B, C, D y E.
>> Acceder a las prestaciones bases de correas trapezoidales (Pb)
5.11- Potencia efectiva por correa
La potencia efectiva por correa (Pe) se calcula a partir de la potencia base (Pb) afectada de los coeficientes correctores por longitud de correa (Fcl) y por arco de contacto (FcA). De esta forma la expresión que proporciona la potencia efectiva es la siguiente:
Pe = Pb · Fcl · FcA
5.12- Cálculo del número de correas
El cálculo del número de correas necesaria para mover la transmisión es inmediato y resulta de dividir la potencia corregida (Pc) vista en el apartado 5.2 y que constituye el total de la potencia a transmitir, entre la potencia efectiva (Pe) por correa. Es decir, que:

ANEXOS
A.1- Ejemplo de cálculo
• Datos de partida
- Máquina conductora:
Motor diesel monocilíndrico
Potencia: 10 HP
Revoluciones (N): 3600 rpm
Diámetro polea salida: 125 mm.
- Máquina conducida:
Bomba centrífuga de aguas limpias
Caudal: 90 m3/h
Revoluciones (n): 1500 rpm
Diámetro polea conducida: a determinar
• Potencia transmitida (Pc)
Pc = P · K, donde
P = 10 HP
K = 1,2 es el factor de corrección de la potencia (ver tabla 11 del apartado 5.2)
Sustituyendo resulta,
Pc = 12 HP
• Selección del tipo de correa
Entrar en la tabla de la Figura 14. "Selección de la sección de la correa" del apartado 5.3, con los siguientes valores:
- N= 3600 rpm, velocidad de giro de la polea menor;
- Pc= 12 HP.
Tipo de correa seleccionada: Perfil "A"
• Relación de transmisión (R)
La relación de transmisión se calcula de acuerdo a lo mostrado en el apartado 5.4:
R = N / n = 3600 / 1500 = 2,4
• Diámetros de las poleas
Diámetro polea menor (d): 125 mm, que es válida según la Tabla 8 (apartado 4.2) para correa de perfil "A" seleccionado.
Diámetro polea mayor (conducida, D)= 125 · 2,4= 300 mm
• Distancia entre ejes de poleas
Aplicando la formulación del apartado 5.6, la distancia entre ejes mínima resulta ser de Emín= 338 mm.
Luego la distancia entre ejes de la máquina conductora y la conducida debe ser E ≥ 338 mm.
Se selecciona como distancia entre ejes válida, E = 500 mm.
• Longitud de la correa
En el apartado 5.7 se puede acceder a la formulación que proporciona la longitud exacta que debe tener la correa (Lp), en función de la distancia entre ejes de poleas (E= 500 mm), el diámetro de la polea menor (d= 125 mm) y el diámetro de la polea mayor (D= 300 mm).
Aplicando los valores anteriores resulta Lp= 1722 mm.
Accediendo a la tabla del apartado 5.7 de longitudes nominales se selecciona la más próxima al valor calculado para el tipo de perfil "A".
Se selecciona una correa de perfil "A" con desarrollo nominal 1742 mm (Nº 67).
• Factor de corrección del largo de la correa (Fcl)
En el apartado 5.7 se puede acceder a la tabla que proporciona el Factor de corrección por longitud (Fcl).
Vista la tabla para la longitud seleccionada resulta Fcl= 0,99.
• Cálculo del arco de contacto
En el apartado 5.8 se muestra la expresión para calcular el ángulo de contacto (A) sobre la polea menor, en función de la distancia entre ejes (E= 500 mm), el diámetro de la polea menor (d= 125 mm) y el diámetro de la polea mayor (D= 300 mm).
Aplicando los valores anteriores resulta A= 160º.
• Factor de corrección del arco de contacto (FcA)
En el apartado 5.8 se puede acceder a la tabla que proporciona el Factor de corrección del arco de contacto (FcA).
Vista la tabla para el arco de contacto sobre la polea menor de 160º resulta FcA= 0,95.
• Velocidad de la correa
En el apartado 5.9 se puede acceder a la formulación que proporciona la velocidad lineal de la correa en función del diámetro de la polea menor (d= 125 mm) y sus revoluciones de giro (N= 3600 rpm).
Aplicando los valores anteriores resulta una velocidad lineal de la correa de vt = 23,56 m/s.
El valor obtenido para la velocidad lineal de la correa es válido al ser inferior a los 30 m/s.
• Prestación base de la correa
La prestación base o potencia base (Pb) de la correa puede ser consultada en las tablas del fabricante disponibles en el apartado 5.10.
En dichas tablas, entrando con el diámetro de la polea menor (d= 125 mm) y sus revoluciones de giro (N= 3600 rpm), se obtiene la prestación base para la correa de perfil "A" seleccionada.
Pb = 5,17 HP, resultante de sumarle a la prestación base de la correa de perfil "A" (4,56 HP) la prestación adicional por relación de transmisión (0,61 HP)
• Potencia efectiva por correa
La potencia efectiva por correa (Pe) se calcula a partir de la potencia base (Pb) afectada de los coeficientes correctores por longitud de correa (Fcl) y por arco de contacto (FcA) mediante la expresión siguiente vista en el apartado 5.11:
Pe = Pb · Fcl · FcA = 5,17 · 0,99 · 0,95 = 4,86 HP
• Cálculo del número de correas
Según el apartado 5.12 el número de correas necesarias se calcula mediante la expresión siguiente:
Nº de correas = Pc / Pe = 12 / 4,86 = 2,47
Luego serán necesarias 3 correas.
• Resultado final
La transmisión resultante será la siguiente:
- Tipo correa: A67
- Nº de correas: 3
- Diámetro polea menor: 125 mm
- Diámetro polea mayor: 300 mm
- Distancia entre centros de poleas: 500 mm
>> FIN DEL TUTORIAL
Programa de Colaboración
Ahora puedes colaborar en el sostenimiento de esta web realizando un pequeño donativo
Gracias por tu colaboración
Hermenegildo Rodríguez Galbarro
Editor y Responsable de esta Web. [+info]
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055
