— Tutorial nº 127 —
Transmisión por Cadenas
Cálculo y diseño
Índice de contenidos:
1- Introducción
1.1- Generalidades
1.2- Tipos de cadenas
2- Caracterización del sistema
2.1- Análisis cinemático
2.2- Transmisión de esfuerzos
2.3- Potencia transmitida
3- Ejemplo de cálculo de una cadena de transmisión
ANEXOS:
Anexo nº 1.- Principales fórmulas para el cálculo de cadenas de transmisión
Anexo nº 2.- Tabla de características para cadena simple de rodillos
Anexo nº 3.- Aletas normalizadas para cadenas de rodillos
Anexo nº 4.- Piñones y ruedas normalizadas
Anexo nº 5.- Tabla de velocidades máximas en cadenas
Anexo nº 6.- Tabla de presiones máximas admisibles en articulaciones de cadenas
DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Generalidades
Las cadenas de transmisión son la mejor opción para aplicaciones donde se quiera transmitir grandes pares de fuerza y donde los ejes de transmisión se muevan en un rango de velocidades de giro entre medias y bajas.

Las transmisiones por cadenas son transmisiones robustas, que permiten trabajar en condiciones ambientales adversas y con temperaturas elevadas, aunque requieren de lubricación. Además proporcionan una relación de transmisión fija entre las velocidades y ángulo de giro de los ejes de entrada y salida, lo que permite su aplicación en automoción y maquinaria en general que lo requiera.
Según su función a desarrollar, las cadenas se dividen en los siguientes tipos:
• Cadenas de transmisión de potencia: cuya aplicación es transmitir la potencia entre ejes que giran a unas determinadas velocidades.
• Cadenas de manutención: o también llamadas cadenas transportadoras. Son un tipo de cadenas que gracias a una geometría específica de sus eslabones o enlaces le permiten desempeñar una función de transporte o arrastre de material.
• Cadenas de carga: o también llamadas de bancos de fuerzas. Son cadenas que permiten transmitir grandes cargas, y son usadas, por ejemplo, para elevar grandes pesos, o accionar bancos de fuerza, entre otros usos.
1.2- Tipos de cadenas
Según la geometría que presenten los eslabones o enlaces que conforman las cadenas, y dentro de la división entre cadenas de transmisión de potencia, de manutención y de carga, éstas pueden ser a su vez de diversos tipos, como se expone a continuación:
- Cadenas de transmisión de potencia:

Figura 2. Cadena de casquillos fijos
En el tipo anterior de cadenas de casquillos fijos, el casquillo no rota ni gira respecto a las placas interiores de la cadena.

Figura 3. Cadena de bujes

Figura 4. Cadena de rodillos
En las cadenas de rodillos se monta un rodillo cilíndrico adicional montado sobre el casquillo de la cadena. Los rodillos se montan sueltos, de manera que pueden girar libremente sobre el casquillo. Esto mejora el rozamiento entre la cadena y la rueda dentada sobre la que engrana.
A continuación, se adjunta dos tipos de cadenas de transmisión de potencia que ofrecen un funcionamiento más silencioso y uniforme (figuras 5 y 6). No obstante, estos tipos no son recomendables para transmitir grandes pares de fuerza ni velocidades de giros elevadas, dada el riesgo que existe de desengranar la cadena de transmisión de la rueda dentada.

Figura 5. Cadena silenciosa de casquillos o cadena Gale

Figura 6. Cadena silenciosa con pasador de media caña
- Cadenas de manutención y transportadoras:

Figura 7. Tipos de Cadenas de Manutención
- Cadenas de carga:
La misión principal de las cadenas de carga es la de poder transmitir elevados niveles de esfuerzos. Para ello debe disponer de una mayor sección resistente que las cadenas de transmisión normales. Esto se consigue añadiendo más placas que unan los eslabones de la cadena.
A continuación se incluyen algunos tipos de cadenas de carga.

Figura 8. Tipos de Cadenas de Carga
2- Caracterización del sistema
2.1- Análisis cinemático
En toda cadena de transmisión, cada vez que se produce el engrane de un eslabón con la rueda dentada, se produce una variación tanto en la trayectoria como la velocidad del eslabón. Es lo que se conoce como "efecto poligonal".

Figura 9. Movimiento de la cadena sobre la rueda dentada
En la figura anterior b, B representan puntos pertenecientes a la rueda y a la cadena respectivamente, ω es la velocidad angular a la que gira la rueda dentada y Dp es su diámetro primitivo.
La velocidad lineal de la rueda (vb) viene expresada en función de su velocidad angular de giro (ω) y su diámetro primitivo (Dp) como,
|
Dp · ω |
|
vb = |
|
|
|
2 |
|
Por otro lado, y debido al llamado efecto poligonal, la proyección horizontal de la velocidad del punto B de la cadena (vBx) varía a lo largo del arco de engrane. Esta variación de la velocidad horizontal de la cadena se hace menor conforme aumenta el número de dientes (z) de la rueda.
En efecto, si aumenta el número de dientes (z) de la rueda, el ángulo a entre dientes disminuye, por lo que la geometría poligonal tiende a semejarse a una circunferencia, y el llamado efecto poligonal se atenúa por lo que la variación horizontal de la velocidad de la cadena (vBx) a lo largo del arco de engrane se hace menor.
No obstante, el número de dientes de la rueda no puede aumentar en demasía, dado que esto supone que la altura de los mismos se hace más pequeña y la posibilidad de desengranar la cadena, es decir, que se salga la cadena de la rueda dentada, será mayor.
En la práctica se suelen emplear los siguientes número de dientes tanto para la rueda menor (piñón) como para la rueda mayor:
Tabla A. Número de dientes, z |
|
Piñón o rueda menor |
17 - 19 - 21 - 23 - 25 |
Rueda mayor |
38 - 57 - 76 - 95 - 114 |
2.2- Transmisión de esfuerzos
El valor del esfuerzo que transmite la cadena es máximo en la primera articulación del eslabón que engrana con la rueda por el ramal tenso de la cadena, y a partir de ahí este esfuerzo va gradualmente decreciendo conforme avanza por el arco de engrane hasta salir de la rueda por el ramal de la cadena que está menos tensado.
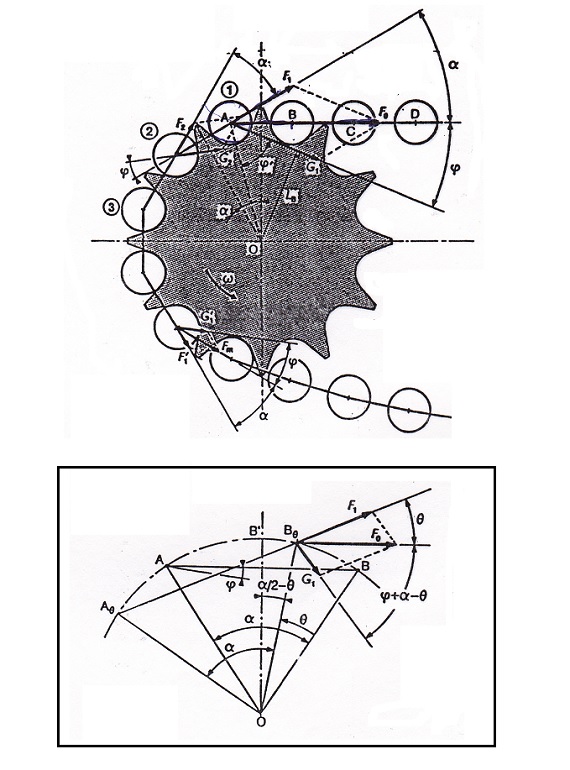
Figura 10. Esfuerzos durante el engrane de la cadena en la rueda
Si F0 es el esfuerzo máximo que soporta la cadena y que se origina en la primera articulación de la misma al engranar con el primer diente de la rueda al entrar en contacto, el esfuerzo que soporta la cadena en las siguientes articulaciones viene expresado por la siguiente formulación:
|
sen φ |
|
Fn = F0 · [ |
———— ] n |
|
|
sen(α+φ) |
|
Siendo n el número de articulación de la cadena.
Por otro lado, la cadena origina una reacción sobre la rueda dentada al engranar en los dientes, que viene expresada por:
|
sen φ |
|
Gn = F0 · [ |
———— ] n-1 |
|
|
sen(α+φ) |
|
Ambos valores, tanto esfuerzos entre las articulaciones de la cadena (Fn) como las reacciones sobre la rueda (Gn), van decreciendo paulatinamente desde el ramal tenso de la cadena hacia el ramal menos tenso.
Se comprueba que en una de las articulaciones la reacción (Gn) sobre la rueda llega a ser radial, es decir, la articulación de la cadena aprieta el fondo de la rueda. En el resto de articulaciones la reacción de la cadena sobre la rueda se realiza sobre el flanco de los dientes.
El desgaste progresivo de los dientes hace que la reacción sobre el flanco se realice cada vez a una mayor altura, llegando el momento en que al ser la holgura tan importante la cadena salte el diente y se salga de la rueda.
Por otro lado, la composición del esfuerzo total (F0) que soporta la cadena, incluye a su vez los siguientes tipos de esfuerzos según el origen:
1º.- Una componente útil o esfuerzo útil asociado al par transmitido (Fu);
2º.- Otra componente del esfuerzo asociado a la fuerza centrífuga de la cadena (Fc);
3º.- Una última componente asociada al peso propio de la cadena o esfuerzo de la catenaria (Fp). Esta componente del esfuerzo en las cadenas de transmisión de potencia que suelen ser más corta es despreciable, pero en las cadenas de manutención y de carga, que son más largas y pesadas, habrá que considerarlo.
El esfuerzo total (F0) en la cadena se obtiene sumando las componentes anteriores:
F0 = Fu + Fc + Fp
En el anexo A.1 que incluye las principales fórmulas de cálculo de las cadenas de transmisión se puede consultar la formulación que proporciona los valores de las distintas componentes del esfuerzo: Fu , Fc y Fp.
2.3- Potencia transmitida
La potencia transmitida por la cadena viene determinada por el esfuerzo útil (Fu) y su velocidad lineal promedio (v):
P = Fu · v
Siendo (Fu) el esfuerzo útil asociado al par de fuerza transmitido, y (v) la velocidad lineal promedio de la cadena, que a su vez puede ser expresada en función de la velocidad angular de giro (ω) y el diámetro primitivo (Dp) de la rueda dentada como,
|
Dp · ω |
|
v = |
|
|
|
2 |
|
No obstante, para el cálculo y diseño de las cadenas de transmisión se usará la potencia corregida de cálculo (Pc), obtenida a partir de la potencia transmitida (P) anterior afectada por unos coeficientes que tendrá en cuenta diversos aspectos del montaje y uso de la cadena:
Pc = K1 · K2 · K3 · K4 · K5 · P
A continuación se expone cómo obtener los valores de los anteriores coeficientes:
- Coeficiente K1:
Tiene en cuenta que el número de dientes de la rueda pequeña o piñón sea distinto de 19. En efecto, si el número de dientes del piñón es igual a 19 el coeficiente (K1) toma de valor la unidad (K1 = 1). En caso contrario, se puede tomar como primera aproximación para el valor de (K1) la proporcionada por la siguiente expresión:
|
19 |
|
K1 = |
|
|
|
z |
|
Siendo (z) el número de dientes de la rueda pequeña o piñón.
Como segunda opción para calcular el coeficiente (K1) se puede emplear la siguiente tabla:

Tabla 1. Coeficiente K1
- Coeficiente K2:
Es el coeficiente de multiplicidad que tiene en cuenta el número de cadenas empleadas en la transmisión (si es simple, es decir, con una cadena, o bien si es una transmisión con doble cadena, o triple...)

Tabla 2. Coeficiente K2
- Coeficiente K3:
Tiene en cuenta el número de eslabones o enlaces que conforman la cadena.

Tabla 3. Coeficiente K3
Siendo n el número de eslabones o enlaces de la cadena y N es el número de ruedas de la transmisión.
- Coeficiente K4:
Es el factor de servicio que tiene en cuenta las condiciones en que trabaja la transmisión:

Tabla 4. Coeficiente K4
- Coeficiente K5:
Es el coeficiente de duración en función de la vida útil prevista para la cadena.

Tabla 5. Coeficiente K5
Una vez obtenido los valores de los distintos coeficientes se calcula el valor de la potencia corregida de cálculo (Pc) a partir de la expresión siguiente como ya se ha visto:
Pc = K1 · K2 · K3 · K4 · K5 · P
Con el valor de la potencia corregida de cálculo (Pc) obtenida y la velocidad de giro de la rueda pequeña o piñón se entra en las siguientes tablas de las que se obtiene la serie y tipo de cadena necesaria y su paso.

Tabla 6. Diagramas para la selección de cadenas de transmisión de potencia
3- Ejemplo de cálculo de una cadena de transmisión
Como aplicación práctica de lo anterior, en este capítulo se tratará de calcular una transmisión por cadenas que conecta un motor eléctrico (máquina motriz) con un compresor de aire de pistón (máquina conducida) y que responda a las siguientes características técnicas como datos de entrada:
- Accionamiento: mediante motor eléctrico dotado de un motorreductor en el eje de salida consistente en un sinfín-corona a 600 r.p.m. (revoluciones por minuto)
- Potencia del motor eléctrico: 28 kW.
- Máquina accionada: compresor de aire de 1 pistón, con eje de entrada a 200 r.p.m. (aprox.)
- Relación de transmisión: 3
- Duración vida útil estimada: 15000 horas.
- Distancia entre centros de ruedas de la transmisión: 1500 mm (aprox.)
1) Número de dientes de las ruedas de la transmisión:
Como la relación de transmisión entre la máquina conductora y conducida es de 3, de la Tabla A del apartado 2.1, se selecciona el número de dientes para ambas ruedas de entra las recomendadas en la tabla y que mejor se aproxime a la relación de transmisión que se necesita:
• Número de dientes rueda menor (piñón), z1 = 25
• Número de dientes rueda mayor, z2 = 76
Relación de transmisión obtenida, r = 76 / 25 = 3,04
2) Cálculo de la potencia corregida de cálculo (Pc):
La potencia corregida de cálculo (Pc), obtenida a partir de la potencia transmitida (P) se calcula a partir de la siguiente expresión vista en el apartado 2.3:
Pc = K1 · K2 · K3 · K4 · K5 · P
donde,
P = 28 kW, es la potencia que transmite la máquina conductora.
Los coeficientes correctores se calcula de las tablas vistas en el apartado 2.3.
- Coeficiente K1:
El coeficiente se puede obtener de la siguiente expresión:
K1 = 19 / z1
Siendo (z1) el número de dientes de la rueda pequeña o piñón. En este caso,
K1 = 19 / z1 = 19 / 25 = 0,76
El coeficiente también se puede obtener de la Tabla 1, entrando con el número de dientes del piñón.
- Coeficiente K2:
Es el coeficiente de multiplicidad que tiene en cuenta el número de cadenas empleadas en la transmisión, que en este caso al tratarse de una cadena simple vale la unidad, según la tabla 2.
K2 = 1
- Coeficiente K3:
Tiene en cuenta el número de eslabones o enlaces que conforman la cadena. En esta primera iteración del cálculo, al carecer de información sobre la longitud que saldrá de la cadena, se va a suponer una cadena de 120 eslabones, con lo que el coeficiente toma el valor unidad, según la tabla 3.
K3 = 1
Posteriormente, y una vez que se calcule la distancia real que resulta entre centros de ruedas y obtenidos sus diámetros se podrá conocer la longitud exacta de la cadena, con lo que habrá que volver a este punto para obtener el coeficiente (K3) con más exactitud.
- Coeficiente K4:
Es el factor de servicio. En este caso al tratarse de un motor eléctrico como máquina conductora o motriz, y de un compresor de aire a pistón como máquina conducida, de la tabla 4 resulta un coeficiente de servicio de valor:
K4 = 1,8
- Coeficiente K5:
Es el coeficiente de duración en función de la vida útil prevista para la cadena. En este caso, se supone una duración de 15000 horas, por lo que de la tabla 5 resulta un coeficiente de:
K5 = 1
Una vez calculados todos los coeficientes ya se puede obtener la potencia corregida de cálculo (Pc):
Pc = K1 · K2 · K3 · K4 · K5 · P = 0,76 · 1 · 1 · 1,8 · 1 · 28 = 38,3 kW
3) Selección del tipo de cadena:
La selección del tipo de cadena se realiza utilizando la tabla 6 del apartado 2.3 y entrando en ella con los siguientes valores:
• Potencia corregida de cálculo (Pc): 38,3 kW;
• Cadena simple;
• Velocidad de giro del piñón: 600 r.p.m.
Con estos valores resulta una cadena Tipo 20B; de paso, p = 31,75 mm.
4) Cálculo del diámetro de las ruedas:
Según la lista de formulaciones que aparecen en el anexo A1 se puede obtener los diámetros primitivos (Dp) de las ruedas mediante la expresión:
|
p |
|
Dp = |
|
|
|
sen (π / z) |
|
donde,
p, es el paso en mm.
z, es el número de dientes.
En este caso se tiene que:
- Rueda piñón:
|
31,75 |
|
Dp1 = |
————— = 253,32 mm |
|
|
sen (π / 25) |
|
- Rueda Mayor:
|
31,75 |
|
Dp2 = |
————— = 768,30 mm |
|
|
sen (π / 76) |
|
5) Cálculo de la longitud de la cadena (L):
Mediante la siguiente expresión se puede calcular la longitud total (L) de la cadena:
|
L ( z1 + z2 ) β 2 |
|
|
—— = ———— + ( z2 - z1 ) · —— + O1O2 · cosβ · —— |
|
|
p 2 π p |
|
donde,
L, es la longitud total de la cadena en mm;
p, es el paso de la cadena, en mm;
z1, es el número de dientes del piñón;
z2, es el número de dientes de la rueda mayor;
O1O2, es la distancia entre centros de las ruedas, en mm;
β, es el ángulo de contacto, en radianes. Analíticamente se obtiene a partir de la siguiente expresión:
|
R2 - R1 |
|
β = sen -1 ( |
———— ) |
|
|
O1O2 |
|
siendo R2 y R1 los respectivos radios de las ruedas mayor y piñón.
La expresión L/p (longitud/paso de la cadena) indica el número de eslabones con que cuenta la cadena, y debe ser un número entero, por lo que habrá que ajustar la distancia entre centros O1O2 para que esto se cumpla. En la siguiente tabla se indican los resultados de aplicar la expresión anterior en un proceso que es iterativo:
O1O2 |
β |
L / p |
1500 |
0,172 |
146,39 |
1495 |
0,173 |
146,08 |
1494 |
0,173 |
146 |
Por lo tanto, se obtiene una cadena de las siguientes características:
• Longitud total (L): 4635,5 mm, que se obtiene multiplicando el número de eslabones obtenidos (146) por el paso (31,75 mm.)
• Distancia entre centros de las ruedas (O1O2): 1494 mm.
Con la longitud real de la cadena (L = 4635,5 mm) y su número de eslabones (n = 146) se recalcula el coeficiente K3 que tiene en cuenta el número de eslabones o enlaces que conforman a la cadena. Volviendo a la tabla 3 resulta,
K3 = 0,8
Con este valor se vuelve a recalcular la potencia corregida de cálculo (Pc):
Pc = K1 · K2 · K3 · K4 · K5 · P = 0,76 · 1 · 0,8 · 1,8 · 1 · 28 = 30,64 kW
De nuevo, la selección del tipo de cadena se realiza utilizando la tabla 6 del apartado 2.3 entrando con los siguientes valores:
• Potencia corregida de cálculo (Pc): 30,64 kW;
• Cadena simple;
• Velocidad de giro del piñón: 600 r.p.m.
Con estos valores resulta de nuevo una cadena Tipo 20B, de paso: 31,75 mm.
6) Comprobación de la velocidad lineal (v):
Según la lista de formulaciones que aparecen en el anexo A1 se puede obtener el valor de la velocidad lineal promedio (v) de la cadena a partir de la siguiente expresión:
|
p · zi · Ni |
|
v = |
|
|
|
60 |
|
donde,
p, es el paso de la cadena
zi, es el número de dientes de la rueda i considerada
Ni, es la velocidad de giro (en r.p.m.) de la rueda i considerada.
En este caso que nos ocupa, si se toma la rueda piñón se tiene que:
p = 31,75 mm (0,03175 m);
z1 = 25 dientes;
N1 = 600 r.p.m.
Por lo que la velocidad lineal de la cadena resulta ser de:
|
0,03175 · 25 · 600 |
|
v = |
————————— = 7,94 m/s |
|
|
60 |
|
Este valor es inferior a los 16 m/s que marca como límite máximo la tabla incluida en el anexo A5 de velocidades máximas en cadenas, que para una cadena de paso 31,75 mm marca los siguientes valores límites:
Paso de la cadena |
Velocidad de giro máxima |
Velocidad lineal máxima |
31,75 |
1600 |
16 |
(*) Extracto de la tabla de velocidades máximas en cadenas del anexo A5
7) Comprobación del esfuerzo total soportado por la cadena:
Según la lista de formulaciones que aparecen en el anexo A1 se puede obtener el valor del esfuerzo útil (Fu) que desarrolla la cadena a partir de la siguiente expresión:
|
P |
|
Fu = |
|
|
|
v |
|
donde,
Fu, es el esfuerzo útil que desarrolla la cadena
P, es la potencia transmitida, en este caso, 28 kW (28000 W)
v, es la velocidad lineal promedio, obtenida en el apartado anterior (7,94 m/s)
Sustituyendo valores resulta un esfuerzo útil de:
|
28000 |
|
Fu = |
———— = 3526 N |
|
|
7,94 |
|
El otro componente del esfuerzo, el debido a la fuerza centrífuga de la cadena (Fc), viene determinado por la siguiente expresión:
Fc = M · v2
Siendo M la masa unitaria (kg/m) de la cadena.
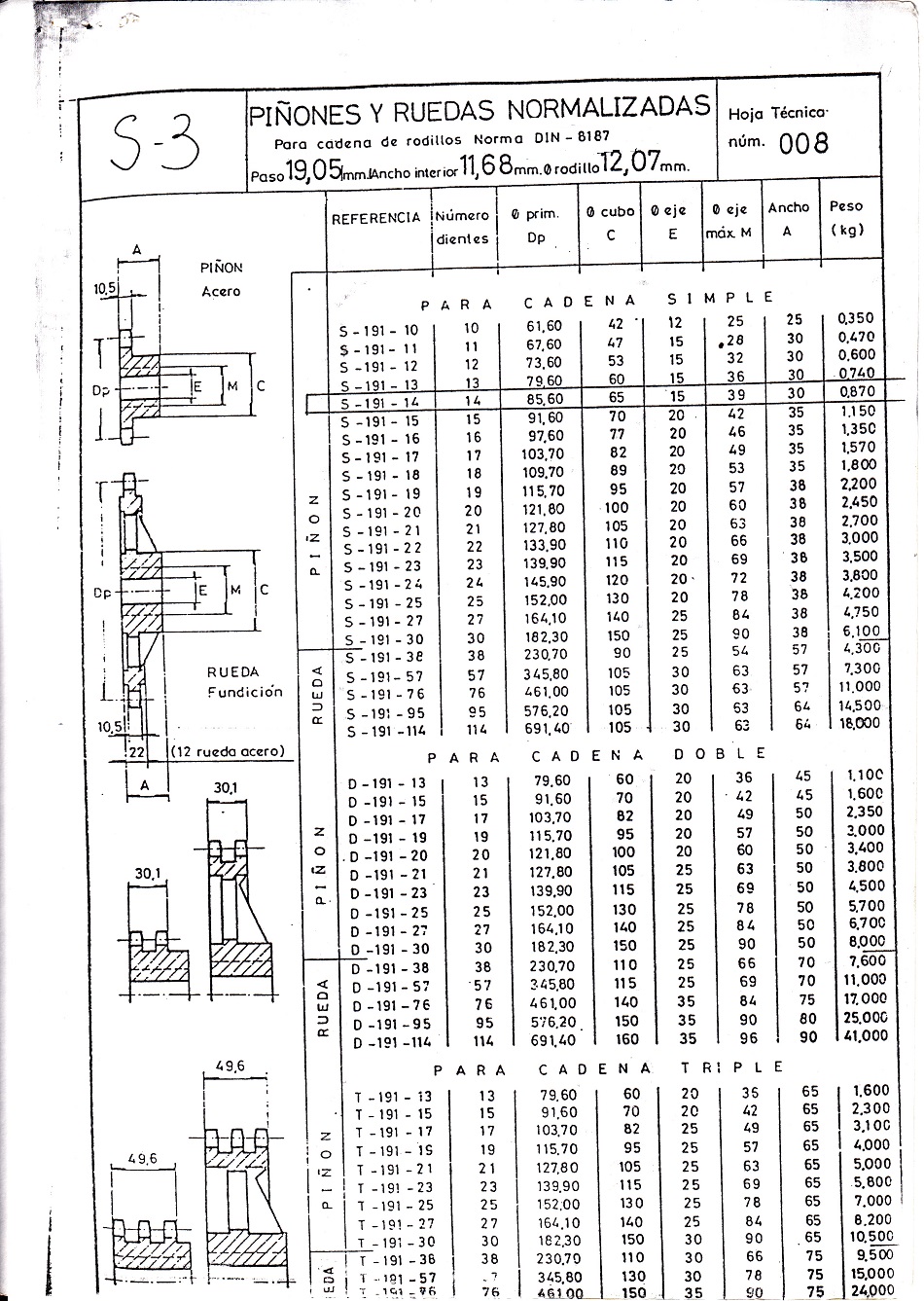
De la tabla de características técnicas para cadena simple de rodillos que se incluye en el anexo A2 se puede obtener que para una cadena Tipo 20B y paso 31,75 mm resultan las siguientes características:
• Peso unitario (M): 3,70 kg/m
• Carga de Rotura (R): 10000 kp
Sustituyendo valores para el caso que nos ocupa resulta un esfuerzo debido a la fuerza centrífuga de la cadena de:
Fc = M · v2 = 3,70 · 7,942 = 233 N
Por lo tanto el esfuerzo total que soporta la cadena vale:
F0 = Fu + Fc = 3526 + 233 = 3759 N (383,31 kp)
Por lo que resulta un coeficiente de seguridad de:
|
R 10000 |
|
Cs = |
—— = ———— = 26 |
|
|
F0 383,31 |
|
Se considera de buena práctica disponer de un coeficiente de seguridad de al menos Cs > 12, por lo que se cumple con la cadena seleccionada.
8) Comprobación de la presión máxima de contacto:
Según la lista de formulaciones que aparecen en el anexo A1 la presión de contacto (Ps) que ejerce la cadena sobre el flanco del diente de la rueda se puede calcular a partir de la siguiente expresión:
|
F0 |
|
Ps = |
|
|
|
d · l |
|
donde,
F0, es el esfuerzo total que transmite la cadena
d, es el diámetro del perno (bulón o eje) de la cadena
l, es la longitud del casquillo de la cadena. En las tablas de características de la cadena que se incluyen en el anexo A2 también aparece como el ancho del eslabón interior.
De nuevo, de la tabla de características técnicas para cadena simple de rodillos que se incluye en el anexo A2 se puede obtener para una cadena Tipo 20B y paso 31,75 mm los parámetros anteriores:
• Diámetro del perno o eje (d): 10,17 mm
• Longitud del casquillo o anchura del eslabón interior (l): 29,01 mm
Sustituyendo, resulta una presión o tensión de contacto de:
|
3759 |
|
Ps = |
——————— = 12,74 MPa |
|
|
10,17 · 29,01 |
|
Valor que es inferior a la PsMáx= 17 MPa, según se puede extraer de la tabla con las presiones máximas admisibles en las articulaciones del anexo A.6.
Por lo tanto, la cadena seleccionada CUMPLE.
- Resultado Final:
- Cadena:
• Serie: 20B
• Paso: 31,75 mm
• Tipo: cadena simple de rodillos
• Desarrollo o longitud: 4635,5 mm
• Nº de eslabones o enlaces: 146
• Distancia entre centros de las ruedas: 1494 mm
- Rueda menor o piñón:
• Número de dientes: 25
• Diámetro primitivo: 253,32 mm
- Rueda mayor:
• Número de dientes: 76
• Diámetro primitivo: 768,30 mm
ANEXOS
Anexo nº 1.- Principales fórmulas para el cálculo de cadenas de transmisión

Anexo nº 2.- Tabla de características para cadena simple de rodillos
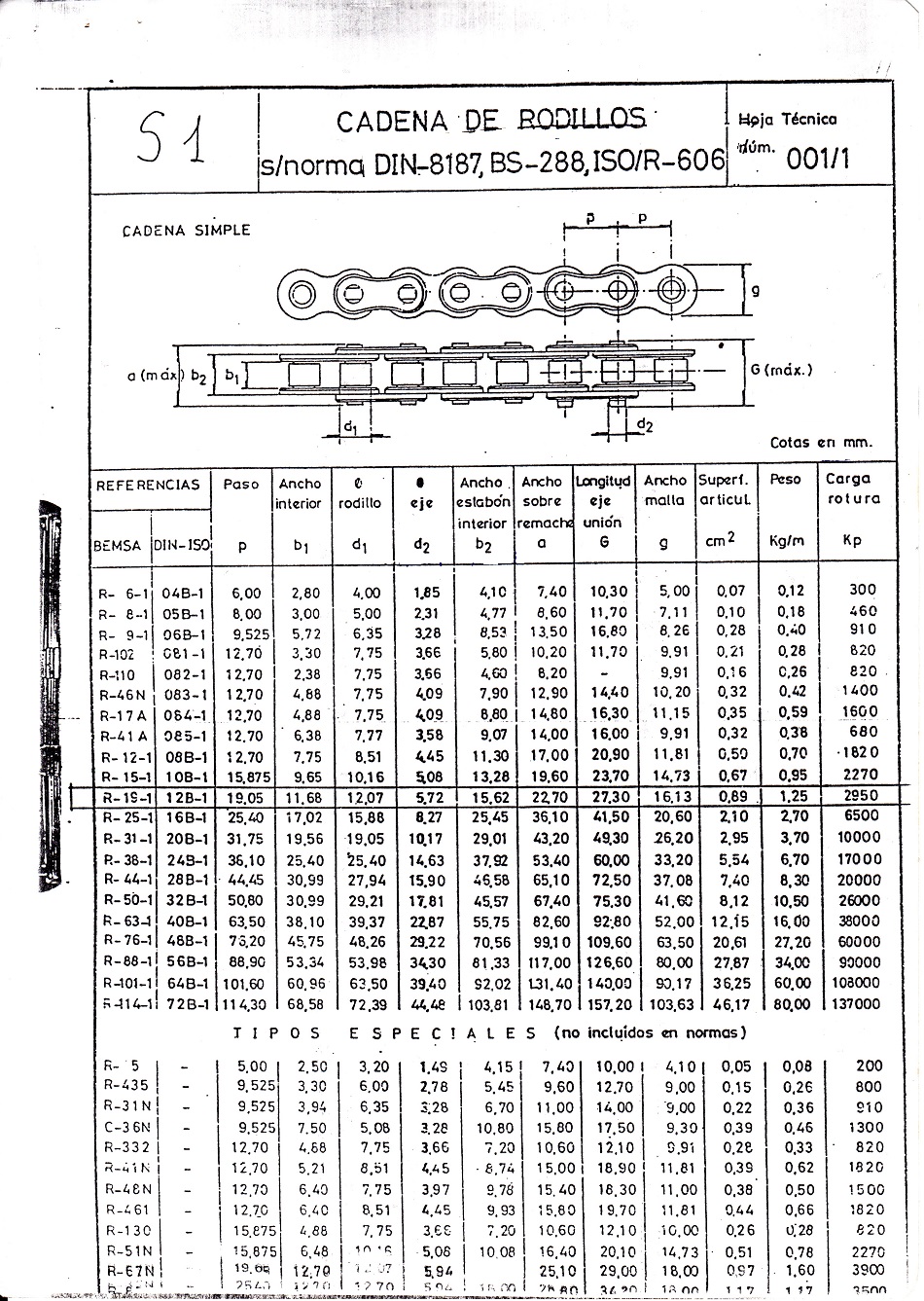
Anexo nº 3.- Aletas normalizadas para cadenas de rodillos
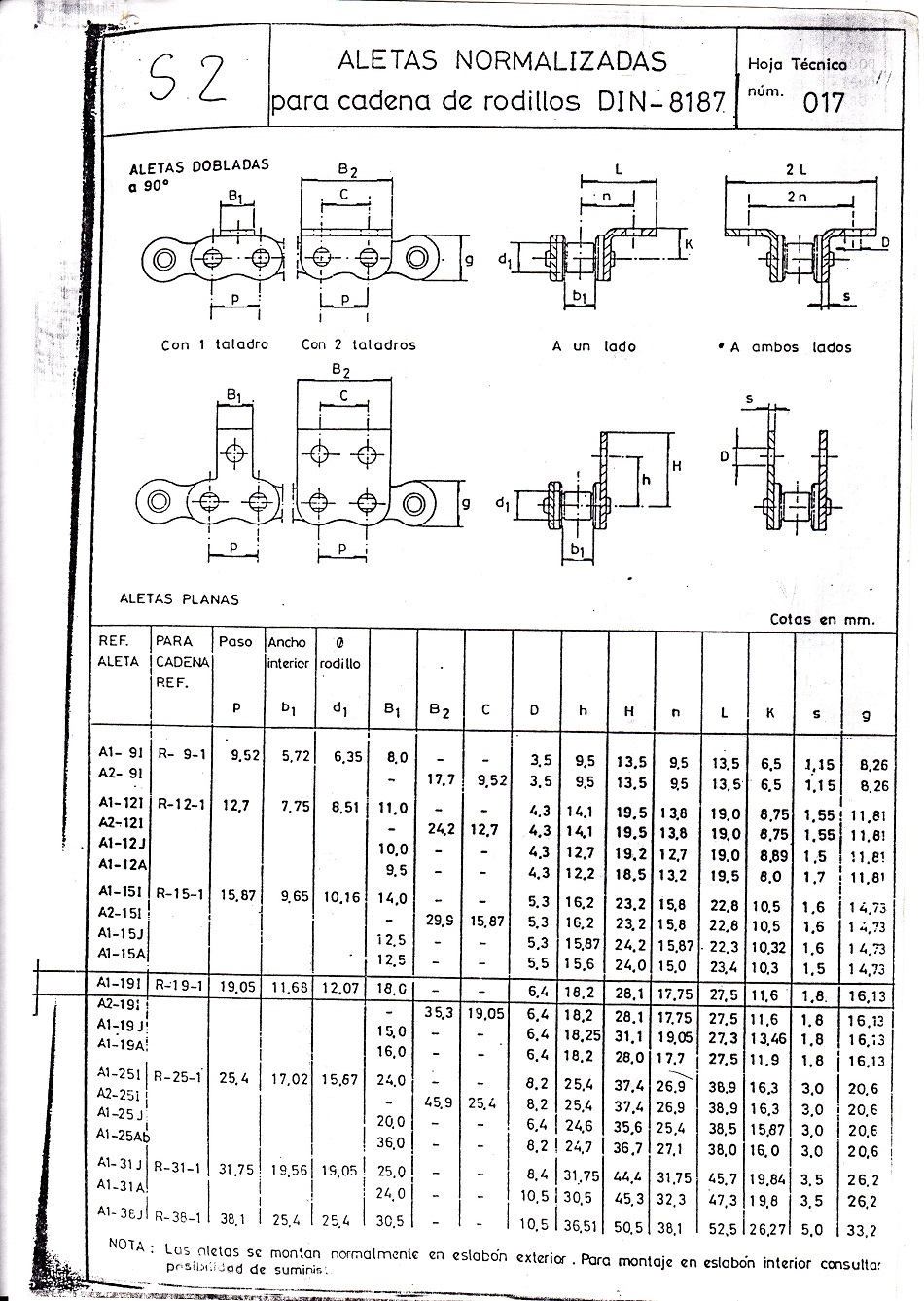
Anexo nº 4.- Piñones y ruedas normalizadas
Anexo nº 5.- Tabla de velocidades máximas en cadenas

Anexo nº 6.- Tabla de presiones máximas admisibles en las articulaciones de cadenas

Programa de Colaboración
Ahora puedes colaborar en el sostenimiento de esta web realizando un pequeño donativo
Gracias por tu colaboración
Hermenegildo Rodríguez Galbarro
Editor y Responsable de esta Web. [+info]
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055
