- Tutorial nº 18 -
Cálculo y diseño de los ejes
de un vehículo
Índice de contenidos:
1- Características constructivas de los ejes
1.1- Generalidades
1.2- Calidades de los aceros
1.3- Geometría del perfil
1.4- Tolerancias
2- Procedimiento de cálculo
2.1- Reparto de cargas sobre los ejes
2.2- Esfuerzos originados en el eje
2.3- Cálculo de las propiedades mecánicas del eje
2.4- Cálculo de las tensiones de trabajo en el eje
2.5- Comprobación final
ANEXO:
Anexo nº 1: Caso práctico de cálculo de un eje supletorio trasero
DESARROLLO DEL CONTENIDO
1- Características constructivas de los ejes
1.1- Generalidades
La importancia en el diseño de los ejes de un vehículo es vital, no sólo en lo que se refiere a la propia seguridad del vehículo y sus ocupantes, sino también en lo referente al buen comportamiento de su conjunto estructural, que se traduce en que si el diseño es correcto, se disminuye la probabilidad que ocurran desgastes prematuros, roturas o fallos de otros componentes y sistemas asociados (suspensión, neumáticos, bastidor…).
Por otro lado, según la posición que ocupe y función que desempeñe los ejes dentro del esquema de un vehículo, sea éste un eje motriz o no, serán de diversos tipos. Así, hay ejes que son direccionales, delanteros o traseros, motrices, ejes para remolques y semirremolques, ejes supletorios, etc.
En esta primera revisión del presente tutorial se va a tratar cómo calcular y diseñar ejes traseros supletorios, que por otro lado resulta ser el caso más habitual que ocurre en empresas de transformación y construcción de carrocerías para vehículos industriales (camiones, furgones…) y de remolques y semirremolques.
La necesidad de instalar un nuevo eje supletorio trasero en un vehículo surge cuando se requiere un aumento de la capacidad de carga, o también cuando se requiere cambiar la caja de carga actual por otra de mayor longitud, lo que a veces implica un aumento de su voladizo trasero que supera los límites legales, y por lo tanto, una manera de solucionar este inconveniente es la instalación de un nuevo eje trasero supletorio.
1.2- Calidades de los aceros
Los tipos de aceros que se empleen en la fabricación de los ejes de los vehículos deben ofrecer unas calidades mínimas requeridas a la función que deben desempeñar y al tipo de solicitaciones a que van a estar sometidos, fundamentalmente a cargas dinámicas.
De esta forma, los aceros empleados para la fabricación de ejes deben ofrecer una capacidad de carga elevada, debido a que van soportar todo el peso del vehículo y su carga. Asimismo deben presentar una superficie externa de gran dureza, de excelente calidad y de gran resistencia al desgaste, dado que sobre los extremos de los ejes irán acoplados los bujes de las ruedas que van a girar sobre rodamientos encajados perfectamente sobre la superficie del eje.
De todo lo anterior, los aceros que mejor se adecuan a este uso son los aceros de medio contenido de carbono (desde SAE 1035 a 1053, o también, los de la serie F12 según UNE-36009). Estos aceros generalmente llevan tratamiento térmico de endurecimiento, mediante procesos de temple y revenido, con lo que se consigue dotar de la dureza y calidad necesaria a su superficie. El tratamiento de revenido a que se somete la pieza, posterior al temple, trata de mejorar la excesiva fragilidad que dota el templado, aún a costa de perder algo de resistencia, pero sirve para introducir en la pieza del eje algo más de tenacidad, sobre todo en su núcleo, necesario para ofrecer un mejor comportamiento ante los esfuerzos de flexión a que estarán sometidos los ejes durante su vida útil.
1.3- Geometría del perfil
La geometría del perfil utilizado para la constitución de los ejes va a depender de su uso y localización dentro del esquema general del vehículo.
En general, los ejes delanteros direccionales suelen ser de tipo doble T forjados, mientras que los ejes traseros motrices serán de tipo circular tubular, con el objetivo de albergar en su interior los palieres traseros de transmisión que conectan a la rueda.
Por otro lado, los ejes traseros supletorios serán realizados por perfiles de acero de sección circular, que pueden ser macizas o tubular.
Por último, para el caso de remolques y semirremolques se suelen utilizar secciones circulares o cuadradas macizas.
1.4- Tolerancias
A la hora de la fabricación de la pieza de un eje, los valores de tolerancia son importantes habida cuenta que es un elemento que debe ser acoplado en otros para formar un conjunto estructural.
La norma ISO distingue dieciocho calidades o grados de tolerancias, que van de la IT01 hasta la IT16, según se muestra en la siguiente tabla de la figura 1 expresadas en micras. Para la fabricación de ejes se utilizan los grados de tolerancia que van de la IT1 a la IT4.
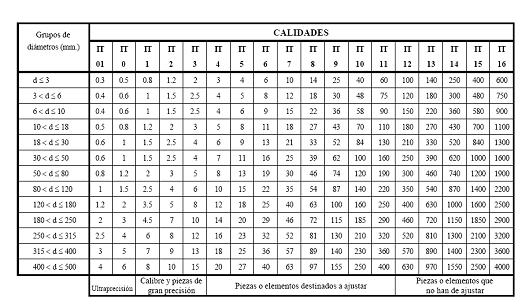
Figura 1. Tabla de tolerancias según calidades (tolerancias en µm)
Evidentemente no será lo mismo tomar el valor de la tolerancia en exceso sobre la medida nominal, o en defecto, es decir, por arriba o por debajo de la medida exacta. Para ello se define lo que se llama la Posición de la Tolerancia, que toma 21 posiciones distintas representadas por letras (minúsculas para los ejes y mayúsculas para los agujeros).
En la siguiente tabla de la figura 2 se representan las 21 posiciones de tolerancias para el caso de los ejes.
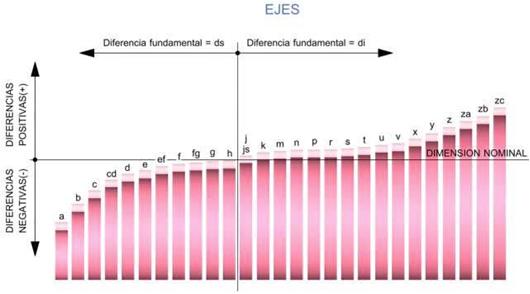
Figura 2. Posiciones de tolerancias para ejes
Como se aprecia en la figura anterior, las posiciones a, b, c, cd, d, e, ef, f, g, h, vienen determinadas por su diferencia superior que es negativa, y va disminuyendo su valor, hasta la h, que es cero. Las posiciones j, k, m, n, p, r, s, t, u, v, x, y, z, za, zb, zc, se fijan por la diferencia inferior, que es siempre positiva a partir de la m.
De esta manera, un ejemplo de denominación ISO de la medida de tolerancia de un eje podría ser la siguiente:
30 h 4
donde,
30 es la medida del diámetro nominal del eje;
h es la posición de la tolerancia;
4 es la calidad de la tolerancia, en este caso IT4, que según la tabla de la figura 1 le corresponde una tolerancia de 6 micras (toda la tolerancia negativa).
2- Procedimiento de cálculo
2.1- Reparto de cargas sobre los ejes
Para el reparto de cargas sobre los ejes del vehículo, que es necesario conocer previamente para poder realizar su posterior diseño, se consideran las siguientes cargas:
- Peso del autobastidor del vehículo sin carrocería, o también llamado peso en chasis-cabina (Q'), siendo R'A y R'B, respectivamente el peso del autobastidor distribuido sobre los ejes delantero y trasero;
- Peso de la carrocería montada o caja de carga montada sobre el chasis del vehículo (Q1);
- Peso máximo admitido de la mercancía a transportar o carga útil (Q2).
Para este tutorial se va a aplicar el caso genérico de vehículos de dos ejes, donde posteriormente se le incorporará un tercer eje trasero supletorio. Para estos vehículos, en posición de marcha y con carga uniformemente repartida sobre la caja de carga, el cálculo de las reacciones sobre los ejes del vehículo delantero (RA) y trasero (RB) se realiza aplicando las siguientes expresiones:
RA= Q · (L/2-a)/p ;
RB= Q · (L/2+m)/p ;
donde:
L, es la longitud de la caja de carga de extremo a extremo;
a, es el voladizo posterior o distancia entre el eje trasero y el extremo de la caja de carga;
p, es la distancia entre los ejes delantero y trasero;
m, es la distancia desde eje delantero al comienzo de la caja de carga;
Q, es la carga considerando el peso del carrozado o caja de carga más la carga útil máxima transportada (Q = Q1 + Q2 )
En la figura adjunta se incluye un croquis de un vehículo tipo donde se indican las anteriores definiciones.
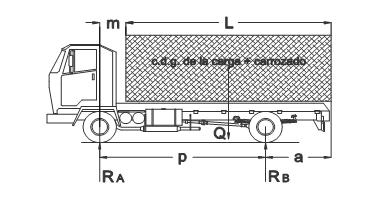
Figura 3. Esquema de vehículo de 2 ejes
No obstante, el reparto total de las cargas sobre los ejes según las expresiones anteriores sólo es aplicable en situación de reposo o en posición de marcha a velocidad constante, pero no en situaciones de aceleración o de frenado, donde las fuerzas de inercia juegan un papel importante y van a originar esfuerzos adicionales en los ejes.
Así, para las situaciones de frenado o de aceleración, se van a originar nuevas solicitaciones sobre los ejes que van a variar en cada caso, según sean ejes delanteros o traseros.
Para el caso que sea sobre el eje delantero, en el caso de una frenada, se origina un sobreesfuerzo adicional, al mismo tiempo que el eje trasero se descarga en la misma cuantía. Y por el contrario, durante una fase de aceleración del vehículo es el eje trasero el que sufre una sobrecarga, mientras que el delantero se descarga en la misma proporción.
Todos estos sobreesfuerzos son debido a la fuerza de inercia (I) que es proporcional a la masa del vehículo y a la aceleración (positiva o negativa) a que se le someta.
En efecto, la fuerza de inercia (I) de la carga del vehículo puede ser calculada por la siguiente expresión:
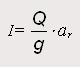
Donde,
Q, es la carga considerando el peso del carrozado o caja de carga más la carga útil máxima transportada (Q1 + Q2);
ar, es la deceleración máxima producida durante la frenada;
g, es la aceleración de la gravedad (9,81 m2/s).
Por otro lado, el valor máximo que puede tomar la deceleración viene dado por la siguiente expresión:
ar = μa · g
donde,
μa, es el coeficiente de adherencia (se suele tomar como seguridad, μa = 1)
A continuación se indican las expresiones que proporcionan estas sobrecargas sobre los ejes delantero y trasero.
• Eje delantero:
Sobre el eje delantero, la sobrecarga que sufre este eje durante los procesos de frenada del vehículo (ΔRA) puede ser calculada por la expresión siguiente:
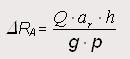
donde,
Q, es la carga considerando el peso del carrozado o caja de carga más la carga útil máxima transportada (Q1 + Q2);
ar, es la deceleración máxima producida durante la frenada;
h, es la altura del centro de gravedad de la carga al pavimento;
g, es la aceleración de la gravedad (9,81 m2/s);
p, es la distancia entre los ejes delantero y trasero.
• Eje trasero:
Por otro lado, para el eje trasero, durante el proceso de aceleración del vehículo éste sufre una sobrecarga (ΔRB), como ya se ha comentado anteriormente. Este valor de la sobrecarga se puede obtener a través de la siguiente expresión:
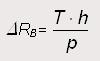
donde,
T, es el esfuerzo tangencial máximo obtenido en las ruedas motrices traseras;
h, es la altura del centro de gravedad de la carga al pavimento;
p, es la distancia entre los ejes delantero y trasero.
Por otro lado, si se designa con R*BT la carga total que recae sobre el eje trasero durante la fase de aceleración del vehículo, ésta tendría la siguiente expresión:
R*BT = R'B + RB + ΔRB
donde,
R'B, es la parte del peso del autobastidor del vehículo que recae sobre ele eje trasero;
RB, es la reacción sobre el eje trasero debido a la carga útil o mercancía transportada y la caja de carga (Q)
ΔRB , es la sobrecarga que se origina sobre el eje trasero debido al proceso de aceleración del vehículo.
La anterior expresión, que recoge la totalidad de las cargas sobre el eje trasero, si es desarrollada queda de la siguiente forma:
R*BT = R'B + RB + (T·h)/p = RBT + (T·h)/p
Siendo RBT = R'B + RB.
Siguiendo con el proceso de desarrollo, el valor del esfuerzo tangencial T que pueden desarrollar las ruedas traseras motrices puede ser expresada por la siguiente formulación:
T = R*BT · μa
Que si se sustituye en la expresión anterior, permite obtener una fórmula para el cálculo del esfuerzo total que recae sobre el eje trasero en la fase de aceleración:
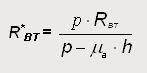
Siendo,
p, es la distancia entre los ejes delantero y trasero;
h, es la altura del centro de gravedad de la carga al pavimento;
μa, es el coeficiente de adherencia (se suele tomar como seguridad, μa = 1)
RBT, es la reacción sobre el eje trasero debido al peso del autobastidor del vehículo más la carga útil o mercancía transportada (RBT = R'B + RB)
2.2- Esfuerzos originados en el eje
Un eje de un vehículo se encuentra sometido a distintos tipos de esfuerzos, a saber:
• Momentos flectores o de flexión del eje;
• Esfuerzos cortantes, que son fuerzas que actúan perpendicular a la dirección longitudinal del eje;
• Y momentos torsores, que para el caso de ejes supletorios traseros, es debido al torsor que origina la fuerza de fricción rueda-suelo que se produce durante la frenada, por ejemplo.
Para el estudio y cálculo de la distribución de momentos y fuerzas a lo largo del eje, hay que partir de las condiciones de contorno o de apoyo que relacionan al eje con el resto del vehículo y con el suelo.
Así, los ejes estarán conectados con el resto del vehículo, en concreto con el bastidor del mismo, a través de la suspensión (ballestas, amortiguadores, muelles…) y con el suelo por su encaje en los bujes de las ruedas.
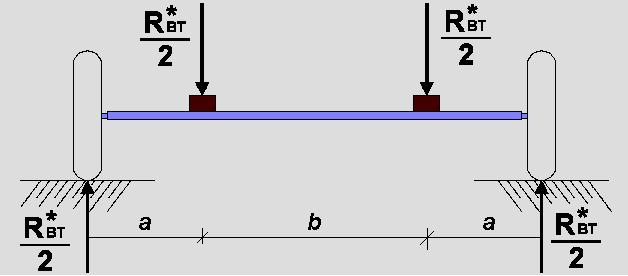
Figura 4. Esquema de solicitaciones sobre un eje
Por lo tanto, para el estudio de la distribución de los esfuerzos a lo largo del perfil del eje, habrá que realizarlo por tramos, según la figura anterior, y de la siguiente manera:
Para x1=0:
V(0)= R*BT/2 ;
Mf(0)= 0;
Para a ≥ x1 > 0:
V(x1)= R*BT/2 ;
Mf(x1)= R*BT/2 · x1;
Para x1= a:
V(a)= R*BT/2 ;
Mf(a)= R*BT/2 · a;
Para a+b > x2 > a:
V(x2)= R*BT/2 - R*BT/2 =0;
Mf(x2)= R*BT/2 · x2 - R*BT/2 · (x2 - a) = R*BT/2 · a;
Para x3=0:
V(0)= - R*BT/2 ;
M(0)= 0;
Para a ≥ x3 > 0:
V(x3)= - R*BT/2 ;
Mf(x3)= R*BT/2 · x3;
Para x3= a:
V(a)= - R*BT/2 ;
Mf(a)= R*BT/2 · a;
GRÁFICO DE ESFUERZOS
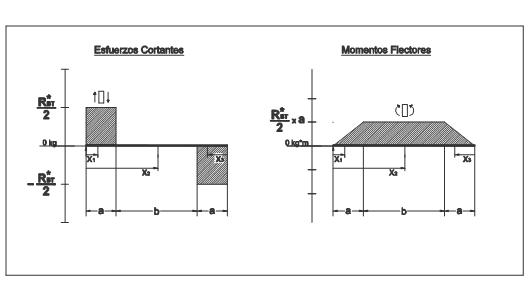
Figura 5. Diagrama de esfuerzos cortantes y flectores
De donde se obtiene que el momento flector máximo resulta ser igual a:
Mf(máximo)= R*BT / 2 · a;
Para calcular el momento torsor más desfavorable sobre el eje supletorio trasero, que es el originado durante la frenada de la rueda, se emplea la siguiente expresión del momento:
MtB= R*BT / 2 · μa · R;
Siendo R el radio de rodadura de la rueda cargada.
El caso más desfavorable se obtiene con un coeficiente de adherencia igual a 1 ( μa = 1 ), con lo que el momento torsor actuante sobre el eje sería:
MtB= R*BT / 2 · R
2.3- Cálculo de las propiedades mecánicas del eje
Una vez calculado los diagramas de esfuerzos que actúan sobre el eje del vehículo, y previo al cálculo de los niveles de tensiones que se alcanza en la sección del perfil para comprobar su idoneidad o no, es necesario conocer sus propiedades mecánicas.
De entre todas las propiedades mecánicas definidas para una sección de un perfil de acero (momentos de inercia respecto a cada uno de los ejes principales, momentos estáticos, área de la sección…) es el módulo resistente a flexión según sus ejes principales (Wx-x) y el módulo resistente a torsión (Wt), los parámetros mecánicos que son necesarios conocer.
El módulo resistente a flexión (Wx-x) de la sección del eje viene dada por la siguiente expresión:
Wx-x= Ix-x / ymáx
donde:
Ix-x es momento de inercia del perfil del eje respecto al eje x-x neutro de la sección;
ymáx es la distancia del eje neutro de la sección a la fibra más alejada de la misma.
Por otro lado, para calcular el módulo resistente a torsión (Wt) se emplea esta otra expresión:
Wt= Io / Rmáx
siendo:
Io es el momento polar, Io = Ixx + Iyy;
Rmáx es la distancia del c.d.g. de la sección del eje a su fibra más lejana.
Estos parámetros están tabulados en las tablas de secciones normalizadas de perfiles, y se pueden consultar en cualquier prontuario.
En el siguiente enlace se puede acceder a los perfiles comerciales de acero y a sus propiedades mecánicas:
>> Acceso al Prontuario de Perfiles de Acero
2.4- Cálculo de las tensiones de trabajo en el eje
Una vez calculado los diagramas de esfuerzos que actúan sobre el eje del vehículo y conocidas sus propiedades mecánicas, el siguiente paso es calcular la tensión de trabajo que está soportando el eje.
Para el cálculo de la tensión de trabajo, se considerarán los esfuerzos de flexión y de torsión como los responsables principales de las solicitaciones sobre el eje.
La tensión de trabajo debido a la flexión del eje viene dada por la siguiente expresión:
σf = Mf(máx) / Wx-x
siendo:
σf es la tensión de trabajo del eje a flexión;
Mf(máx) es el momento flector máximo que actúa sobre el eje;
Wx-x es el módulo resistente a flexión del perfil del eje respecto al eje de flexión.
Por otra parte, el cálculo de las tensiones de torsión (σt), a que estará sometido el eje viene dada por la siguiente expresión:
σt = Mt / Wt
siendo:
σt la tensión de trabajo a torsión del eje;
Mt es el momento torsor que actúa sobre el eje;
Wt es el módulo resistente a torsión del perfil del eje.
Como consecuencia del trabajo simultáneo a flexión y torsión a que está sometido el eje y que originan las correspondientes tensiones de flexión (σf) y torsión (σt), resulta que la tensión final de trabajo será una combinación de ambas, llamada tensión combinada (σco), que viene dada por la expresión:
2.5- Comprobación final
Una vez calculado la tensión combinada de cálculo (σco), la seguridad en el diseño del eje se obtiene comparando esta tensión con el límite elástico del material del eje (σe).
En este caso, para que se considere válido el tipo de perfil elegido para el eje, se debe cumplir la siguiente condición:
λ= σe / σco > 3
Es decir, se considera aceptable el diseño cuando se tenga un factor de seguridad de al menos de 3.
ANEXO:
Anexo nº 1: Caso práctico de cálculo de un eje supletorio trasero
A continuación se expone un caso práctico e ilustrativo de cómo llevar a cabo las comprobaciones de diseño de un eje supletorio trasero.
• Reparto de cargas sobre el eje:
Se parte de un vehículo 4x2 al que se le incorpora un tercer eje trasero supletorio para aumentar su capacidad de carga, por lo que finalmente resulta una configuración 6x2.
a) Configuración inicial 4x2:

b) Configuración final 6x2:

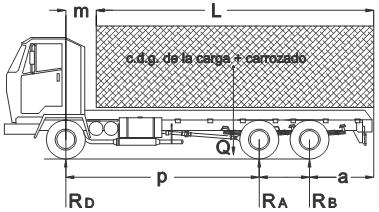
Figura 6. Configuración final 6x2
Por tanto, la carga de diseño que se tomará para el cálculo del tercer eje supletorio, será la máxima admisible, es decir:
RBT = 7.500 kg.
A continuación, para calcular el esfuerzo total que se origina sobre el eje trasero en la fase de aceleración, de acuerdo a lo indicado en el apartado 2.1, se emplea la formulación siguiente:
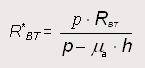
Para el caso que nos ocupa se consideran los siguientes valores para el vehículo:
p, la distancia entre los ejes delantero y trasero, tiene un valor de 5.450 mm;
h es la altura del centro de gravedad de la carga al pavimento, de valor 1.510 mm;
μa es el coeficiente de adherencia (se suele tomar, μa = 1)
RBT toma el valor de la carga máxima admisible en el eje trasero, de valor 7.500 kg.
Sustituyendo en la expresión anterior, resulta una carga final de diseño actuante sobre el eje trasero supletorio de valor igual a:
R*BT = 10.374 kg
• Esfuerzos originados en el eje:
A continuación se indica la distribución de esfuerzos cortantes y momentos flectores y torsores a lo largo del perfil del eje.
Para este caso ilustrativo se supone para el eje los siguientes valores para el ancho de vía y para la distancia entre capuchinos de apoyo de las ballestas de amortiguación:
Ancho de vía: 2.050 mm;
Distancia entre capuchinos: 1.550 mm.
Estas dimensiones suponen, según la Figura 4. Esquema de solicitaciones sobre un eje del apartado 2.2, la siguiente distribución de los esfuerzos a lo largo del perfil del eje:
Para x1=0:
V(0)= R*BT/2 = 5.187 kg;
Mf(0)= 0;
Para a= 250 mm ≥ x1 > 0:
V(x1)= R*BT/2 = 5.187 kg;
Mf(x1)= R*BT/2 · x1 = 5187 · x1, siendo Mf(máx)= 1297 mkg, para x1 = 250 mm (0,25 m);
Para x1= a= 250 mm:
V(a)= R*BT/2 = 5187 kg;
Mf(a)= R*BT/2 · a = 1297 mkg;
Para a+b= 1800 mm > x2 > a= 250 mm:
V(x2)= R*BT/2 - R*BT/2 =0;
Mf(x2)= R*BT/2 · x2 - R*BT/2 · (x2 - a) = R*BT/2 · a = 1297 mkg;
Para x3=0:
V(0)= - R*BT/2 = - 5187 kg;
M(0)= 0;
Para a= 250 mm ≥ x3 > 0:
V(x3)= - R*BT/2 = - 5187 kg;
Mf(x3)= R*BT/2 · x3 = 5187 · x3, siendo Mf(máx)= 1297 mkg, para x3 = 250 mm (0,25 m);
Para x3= a= 250 mm:
V(a)= - R*BT/2 = - 5187 kg;
Mf(a)= R*BT/2 · a= 1297 mkg;
GRÁFICO DE ESFUERZOS
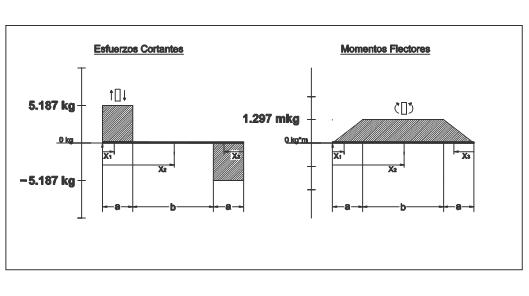
Figura 7. Diagrama de esfuerzos cortantes y momentos flectores
Por lo tanto, el momento flector máximo alcanzado en el eje resulta ser:
Mf(máx)= 1297 mkg.
Para calcular el momento torsor más desfavorable sobre el eje supletorio trasero, que es el originado durante la frenada de la rueda, se emplea, como ya se vio anteriormente, la siguiente expresión del momento:
MtB= R*BT / 2 · μa · R
Siendo R el radio de rodadura de la rueda cargada.
El caso más desfavorable se obtiene con un coeficiente de adherencia igual a 1 (μa = 1), con lo que el momento torsor actuante sobre el eje sería:
MtB= R*BT / 2 · R
Por otro lado, se tiene, que para el caso ilustrativo que nos ocupa, el vehículo monta en todos sus ejes, inclusive en el eje supletorio, neumáticos tipo 315/80R22,5.
El cálculo del diámetro de rodadura de un neumático es inmediato empleando la siguiente expresión:
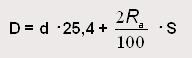
siendo:
Ra = Relación de forma (adimensional);
S = Anchura de la sección del neumático en mm;
d = Diámetro de la llanta en pulgadas;
D = Diámetro exterior en mm, a calcular.
(*) Por favor, para conocer el origen de la expresión anterior se remite al lector a consultar el siguiente tutorial:
>> Tutorial nº 72: ESTUDIO DEL NEUMÁTICO. NORMAS DE DESIGNACIÓN
Aplicado al ejemplo del neumático considerado, resultan los siguientes valores:
Neumático tipo: 315 / 80 R 22,5:
Ra = 80%
S = 315 mm.
d = 22,5 pulgadas.
De este modo resulta que el diámetro exterior del neumático, aplicando la expresión anterior, resulta ser de:
D= 22,5 · 25,4 + 2 · (80/100) · 315 = 1076 mm.
Por lo que el requerido radio de rodadura R vale:
R= 0,5 · D= 538 mm.
Una vez conocido el radio de rodadura del neumático se puede conocer el valor del momento torsor actuante. En efecto:
MtB= R*BT / 2 · R
donde,
RBT es la carga máxima admisible en el eje trasero, 7.500 kg.
R es el radio del neumático, 538 mm (0,538 m)
Por lo que sustituyendo los valores en la expresión anterior, el momento torsor resultante sobre el eje es de:
MtB= 2018 mkg
• Propiedades mecánicas del eje:
Para el diseño de un eje en un vehículo, lo más normal es partir de un tipo de perfil y comprobar si cumple o no, y en caso de cumplir cuál es el coeficiente de seguridad que se obtiene.
Generalmente se considerará que un tipo de perfil es válido cuando el grado o coeficiente de seguridad obtenido bajo las solicitaciones de diseño sean mayor a 3 (λ > 3).
Para este caso práctico, al tratarse de un eje trasero supletorio, se tomará un perfil tubular (perfil circular hueco) de calidad de acero con un límite elástico mínimo de al menos 36 kg/mm2 y con las medidas dimensionales que se indican en la figura siguiente:
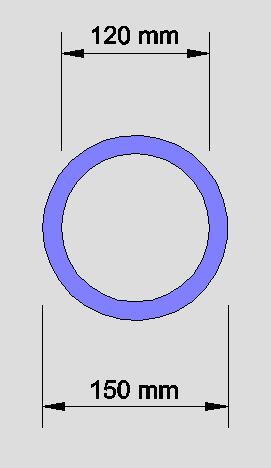
Figura 8. Sección del perfil del eje
(Perfil tubular hueco: diámetro exterior: 150 mm; diámetro interior: 120 mm;)
Según lo descrito en los apartados anteriores, para calcular las tensiones de trabajo a flexión y torsión del eje, es necesario conocer previamente los módulos resistentes a flexión (Wx-x) y a torsión (Wt) de la sección del eje.
- El módulo resistente a flexión (Wx-x) de la sección del perfil del eje respecto a su eje de giro se calcula por la siguiente expresión:
Wx-x = Ix-x / ymáx;
donde:
Ix-x es el momento de inercia del perfil del eje respecto al eje x-x neutro de la sección;
ymáx es la distancia del eje neutro de la sección a la fibra más alejada de la misma.
Para el caso de una sección circula hueca con diámetro exterior de y diámetro interior di, el momento de inercia Ix-x respecto al eje x-x es:
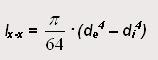
donde,
de = 150 mm;
di = 120 mm;
Por lo que sustituyendo estos valores se tiene que el momento de inercia vale:
Ix-x = 14.671.729 mm4
Por otro lado, la distancia del eje neutro a la fibra más alejada para la sección del perfil es:
ymáx = de / 2= 75 mm ;
Por lo tanto el módulo resistente a flexión (Wx-x) de la sección del perfil del eje respecto al eje de flexión se calcula por la siguiente expresión:
Wx-x = Ix-x / ymáx = 195.623 mm3
- Por otro lado, para calcular el módulo resistente a torsión (Wt) se emplea esta otra expresión:
Wt= Io / Rmáx
siendo:
Io el momento polar, de valor Io = Ixx + Iyy;
Rmáx es la distancia del c.d.g. de la sección del eje a su fibra más lejana.
El momento polar de una sección circular hueca viene dado por la siguiente expresión:
Que sustituyendo los valores de los diámetros exterior e interior de la sección se obtiene el siguiente valor del momento polar:
Io = 29.343.457 mm4
Por otro lado, la distancia del c.d.g. de la sección del eje a su fibra más alejada es:
Rmáx = de / 2= 75 mm
Por lo que sustituyendo valores se obtiene el módulo resistente a torsión de la sección:
Wt= Io / Rmáx = 391.246 mm3
• Cálculo de las tensiones de trabajo en el eje:
Una vez calculado las propiedades mecánicas de la sección del eje y conocidos los valores máximos que se alcanza para los esfuerzos en la situación más desfavorable, las tensiones de trabajo se calculan de manera inmediata a través de las siguientes expresiones:
- Tensión de trabajo a flexión:
La tensión de trabajo debido a la flexión del eje viene dada por la siguiente expresión:
σf = Mf(máx) / Wx-x
siendo:
σf es la tensión de trabajo del eje a flexión;
Mf(máx) es el momento flector máximo que actúa sobre el eje;
Wx-x es el módulo resistente a flexión del perfil del eje respecto al eje de flexión.
De los apartados anteriores se tienen los siguientes valores:
Mf(máx)= 1.297 mkg.
Wx-x = 195.623 mm3
Por lo que la tensión de trabajo a flexión alcanza el valor de:
σf = Mf(máx) / Wx-x = 6,63 kg/mm2
- Tensión de trabajo a torsion:
La tensión de trabajo a torsión (σt), a que estará sometido el eje viene dada por la siguiente expresión:
σt = Mt / Wt
siendo:
σt la tensión de trabajo a torsión del eje;
Mt es el momento torsor que actúa sobre el eje;
Wt es el módulo resistente a torsión del perfil del eje.
De los apartados anteriores se tienen los siguientes valores:
Mt(máx)= 2.018 mkg.
Wt = 391.246 mm3
Por lo que la tensión de trabajo a torsión alcanza el valor de:
σt = Mt / Wt = 5,16 kg/mm2
• Comprobación final:
Para la comprobación final se tomará como referencia la tensión límite de elasticidad para la calidad de acero del perfil del eje. En este caso se toma como límite elástico del acero del eje igual a 36 kg/mm2
Por otro lado, el eje se encuentra sometido a un trabajo simultáneo de flexión y torsión, lo que origina las correspondientes tensiones de flexión (σf) y torsión (σt) en la sección del perfil del eje.
Como consecuencia de lo anterior, para la comparación con el límite elástico del material del eje se tomará una tensión final de trabajo de comparación que será una combinación de ambas, llamada tensión combinada (σco), que viene dada por la expresión:
Sustituyendo los valores obtenidos en el apartado anterior:
σf = 6,63 kg/mm2
σt = 5,16 kg/mm2
Resulta una tensión combinada de valor:
σco = 10,15 kg/mm2
Una vez calculado la tensión combinada de cálculo, la seguridad en el diseño tomado en el eje se obtiene comparando la tensión combinada de cálculo (σco) con el límite elástico del material del eje (σe).
En este caso, el coeficiente de seguridad resulta:
λ= σe / σco = 36/10,15 = 3,5 > 3
Que se considera un valor adecuado y por lo tanto se concluye que la sección tomada para el eje del vehículo es válida.
>> FIN DEL TUTORIAL
Volver a
Tutoriales
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055

