- Tutorial nº 37 -
Cálculo de Uniones con Bulones
Índice de contenidos:
1- Introducción
1.1- Generalidades
1.2- Calidad de acero para bulones
2- Resistencia del bulón
2.1- Generalidades
2.2- A esfuerzo cortante
2.3- A momento flector
2.4- A la acción conjunta de cortante + flector
2.5- Resistencia al aplastamiento de la pieza
3- Ejemplos de cálculo de bulones
3.1- Ejemplo 1: Bulón sometido a esfuerzo cortante
3.2- Ejemplo 2: Bulón sometido a cortante + flector
ANEXO:
Anexo 1- Tablas de Dimensiones y Propiedades de Barras Redondas de Acero Laminado en Caliente
DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Generalidades

Es muy habitual emplear bulones de acero, pernos o pasadores, como elementos para enlazar o unir piezas entre sí, que en ocasiones suelen ser desmontables.
Los bulones son elementos de acero, los cuales han recibido algún tipo de tratamiento térmico para mejorar sus prestaciones mecánicas y durabilidad de uso.
Para facilitar las labores de montaje de estos elementos, son en la mayoría de los casos de geometría cilíndrica y de sección llena para ofrecer la máxima resistencia al montaje.
Como se ha dicho, es muy común su uso para aquellos tipos de uniones entre piezas o componentes mecánicos que se requieren que sean desmontables por sus características de uso.
Un ejemplo muy conocido es el empleo de bulones o pasadores como elemento de unión en los enganches traseros de los vehículos, de manera que permite el acoplamiento del remolque al vehículo tractor, como se ve en el modelo de la figura adjunta.
En este tutorial se va a indicar cómo proceder para realizar el cálculo de comprobación de la resistencia de los bulones que se emplean en uniones entre piezas, de manera que se pueda saber si existe garantía suficiente de seguridad en su uso.
Para ello, se dará a conocer al lector las distintas formulaciones recomendadas para la comprobación de bulones de acero según el tipo de esfuerzo al que se ve sometido el bulón.
Asimismo, se incluirán algunos ejemplos prácticos de comprobación de bulones sometidos a distintos tipos de solicitaciones, para conocer cómo proceder en estos casos.
Pasamos a continuación a estudiar los distintos tipos de acero que pueden emplearse para la fabricación de bulones y las características mecánicas de resistencia que permiten ofrecer.
1.2- Calidad de acero para bulones
En este apartado se indican las calidades de acero utilizadas para la fabricación de bulones y pernos.
En la siguiente tabla se indican los valores del límite elástico (fyb) mínimo y la resistencia última a tracción (fub) del acero empleado en la fabricación del bulón, según el tipo de tratamiento al que ha sido sometido y del diámetro de éste:
Tabla 1. Calidad de acero para bulones |
||||||||||
Estado |
Temple y Revenido |
Normalizado |
||||||||
|
d ≤ 16 mm |
16 mm < d ≤ 40 mm |
40 mm < d ≤ 100 mm |
d ≤ 16 mm |
16 mm < d ≤ 100 mm |
|||||
Designación |
fyb |
fub |
fyb |
fub |
fyb |
fub |
fyb |
fub |
fyb |
fub |
C 22 |
340 |
500 a |
290 |
470 a |
-- |
-- |
240 |
430 |
210 |
410 |
C 25 |
370 |
550 a |
320 |
500 a |
-- |
-- |
260 |
470 |
230 |
440 |
C 30 |
400 |
600 a |
350 |
550 a |
300 (*) |
500 a |
280 |
510 |
250 |
480 |
C 35 |
430 |
630 a |
380 |
600 a |
320 |
550 a |
300 |
550 |
270 |
520 |
C 40 |
460 |
650 a |
400 |
630 a |
350 |
600 a |
320 |
580 |
290 |
550 |
C 45 |
490 |
700 a |
430 |
650 a |
370 |
630 a |
340 |
620 |
305 |
580 |
C 50 |
520 |
750 a |
460 |
700 a |
400 |
650 a |
355 |
650 |
320 |
610 |
C 55 |
550 |
800 a |
490 |
750 a |
420 |
700 a |
370 |
680 |
330 |
640 |
C 60 |
580 |
852 a |
520 |
800 a |
450 |
750 a |
380 |
710 |
340 |
670 |
(*) Aplicable solo hasta bulones de diámetro, d = 63 mm.
2- Resistencia del bulón
2.1- Generalidades
En este apartado se indicará cómo calcular la resistencia de bulones, pernos o pasadores cuando éstos se emplean como elementos de unión entre piezas.
Lo dispuesto en esta sección es aplicable en aquellas uniones entre piezas donde el bulón pueda ser desmontable, o cuando el pasador o bulón quede dispuesto de tal manera que permita libremente un cierto giro relativo entre las piezas que enlaza. En este caso, se recomienda disponer de un casquillo de material resistente a la corrosión, tal como bronce o bronce sinterizado con PTFE, entre el bulón y las piezas a unir cuando sea necesario garantizar el giro de la unión.
En caso contrario, es decir, cuando el bulón no permita ningún giro relativo entre las piezas de manera que el conjunto permanezca rígido, entonces la unión se podrá calcular como una unión atornillada compuesta de un solo tornillo (en este caso, el bulón), siempre y cuando se cumpla que la longitud del bulón (l) sea menor que 3 veces su diámetro (d).
2.2- A esfuerzo cortante
Cuando un bulón esté dispuesto en la unión de tal manera que sólo esté sometido a un esfuerzo cortante (FE,b), o esfuerzo de cortadura, entonces la resistencia (FR,b) de dicho bulón de diámetro " d ", sección transversal "A" y fabricado de un tipo de acero que tenga una resistencia última a tracción fub, viene determinada por la siguiente expresión:
FR,b = 0,6 · A · fub / γMb
donde γMb es el coeficiente parcial para la resistencia del acero del que está fabricado el bulón. En este caso, para uniones con bulón, se tiene que este coeficiente de seguridad vale γMb = 1,25.
Entonces se tendrá que el bulón empleado de diámetro " d " resistirá con garantías a la solicitación (FE,b) que actúa sobre el bulón, si se cumple que:
FR,b > FE,b
donde,
FR,b es la resistencia a cortante del bulón, calculada según la expresión anterior;
FE,b es el valor del esfuerzo cortante que actúa sobre el bulón.
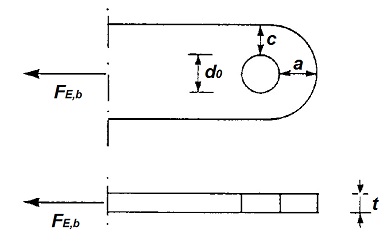
Por otro lado, y una vez comprobado la resistencia del bulón, también habrá que comprobar si las piezas que enlaza el bulón son capaces de resistir igualmente el esfuerzo FE,b actuante.
En efecto, dado una de las piezas enlazadas, tal como se muestra en la figura adjunta, de espesor " t " y unidas a las otras piezas por un bulón de diámetro " d " que se encontrará alojado en el taladro practicado con diámetro " d0 " en la pieza.
Entonces, para que la pieza sea capaz de transmitir con seguridad el esfuerzo FE,b actuante, su geometría, así definida en la figura adjunta, deberá cumplir con las siguientes condiciones:
• Distancia del borde del agujero de la pieza al borde más próximo que sea perpendicular al esfuerzo a transmitir:
| a ≥ | FE,b · γM0 | + | 2 · d0 |
| 2 · t · fy | 3 |
• Distancia del borde del agujero de la pieza al borde más próximo paralelo al esfuerzo a transmitir:
| c ≥ | FE,b · γM0 | + | d0 |
| 2 · t · fy | 3 |
donde γM0 es el coeficiente parcial para la resistencia del acero del que está fabricado la pieza o placa que enlaza el bulón para la sección transversal, cuyo valor para los estados límites últimos vale γM0 = 1,05.
Por otro lado, además se tiene que fy es el límite elástico del acero de la pieza y fu su resistencia última a la tracción.
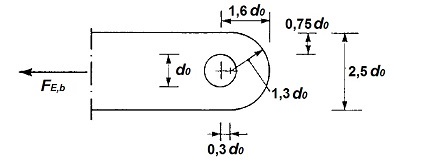
Además de las condiciones geométricas anteriores donde se han definido las distancias mínimas que deben existir desde el borde del taladro a los bordes de la pieza, se deben cumplir otras relaciones entre el diámetro del taladro practicado en la pieza y el espesor de ésta.
En efecto, si " d0 " es el diámetro del taladro practicado en la pieza y " t " es el espesor de la pieza, para que ésta pueda resistir con garantías suficientes el esfuerzo FE,b actuante sobre el bulón alojado en la pieza, entonces se deberá comprobar también que se cumple con los siguientes requisitos:
d0 ≤ 2,5 · t
| t ≥ 0,7 · √ | FE,b · γM0 |
| fy |
En caso de emplearse chapas de refuerzo dispuestas para aumentar el área neta de las piezas o su resistencia al aplastamiento, éstas deberán disponerse sin excentricidad y tendrán el tamaño suficiente para poder transmitir a la pieza el esfuerzo que le corresponda. La unión entre ambas piezas deberá dimensionarse para resistir este esfuerzo.
2.3- A momento flector
En ciertas configuraciones de montaje, se suele enlazar una pieza central (P1) que se encuentra sometida a un esfuerzo (FE,b), con otras dos piezas laterales (P2) separadas una cierta distancia de la pieza central. En este caso, al emplear un bulón para enlazar dichas piezas, éste también se verá sometido a un esfuerzo de flexión.
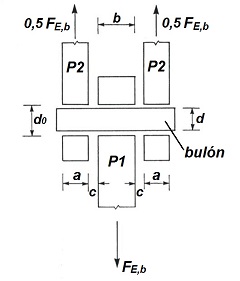
Consideremos la configuración esquemática de la figura adjunta, donde se representa el montaje de una pieza central P1, de espesor " b ", que se encuentra sometida a un esfuerzo FE,b.
Esta pieza central se encuentra enlazada con otras dos piezas laterales P2 que tienen ambas un espesor " a ", por medio de un bulón de diámetro " d ". Dicho bulón atraviesa todas las piezas transversalmente, a las cuales se les ha practicado un taladro con un diámetro del agujero " d0 " para que el bulón pase a través de ellas.
Como se aprecia en la figura adjunta, las piezas laterales se encuentran separadas de la pieza central una distancia " c ".
Pues bien, esta configuración genera también un momento flector ME,b en el bulón cuando sobre la pieza central actúa el esfuerzo FE,b.
Además, el valor de este momento flector que se produce en el bulón se puede calcular mediante la siguiente expresión:
ME,b = FE,b · (b + 4c + 2a) / 8
De esta manera, para que el bulón con diámetro " d ", módulo resistente " W " y fabricado con un acero de límite elástico " fyb " resista con garantías al momento flector, se deberá cumplir la siguiente condición:
ME,b ≤ 1,5 · W · fyb / γMb
donde γMb es el coeficiente parcial para la resistencia del acero del que está fabricado el bulón. En este caso, para uniones con bulón, se tiene que γMb = 1,25.
De la anterior expresión, se obtiene de este modo el momento resistente a flexión del bulón (MR,b) de valor:
MR,b = 1,5 · W · fyb / γMb
Donde el módulo resistente (W) de la sección del bulón, que al ser una pieza cilíndrica, viene dada por la siguiente expresión:
|
I |
|
W = |
|
|
|
d / 2 |
|
donde,
I es el momento de inercia de la sección del eje del bulón, de valor I = (π·d4)/64, siendo d el diámetro del bulón.
Por lo que el módulo resistente (W) del bulón se puede calcular finalmente como:
|
π · d3 |
|
W = |
|
|
|
32 |
|
2.4- A la acción conjunta de cortante + flector
Para los casos donde el bulón de acero esté sometido simultáneamente a la acción combinada de un esfuerzo cortante (FE,b), y de un momento flector (ME,b), entonces se deberá cumplir la siguiente relación, para que la resistencia que ofrezca el bulón en la unión sea suficiente:
( ME,b / MR,b )2 + ( FE,b / FR,b )2 ≤ 1
siendo (MR,b) el momento flector resistente y (FR,b) la resistencia a cortante del bulón, que se calcula según las expresiones dadas en los apartados anteriores.
2.5- Resistencia al aplastamiento de la pieza
En este apartado se mostrará cómo calcular la resistencia al aplastamiento de la pieza en contacto con el bulón.

En efecto, sea una pieza como la de la figura adjunta de espesor " t ", fabricada con un acero de límite elástico " fy " que cuenta con un taladro de diámetro "d0" por donde pasará un bulón de diámetro "d" (d<d0) fabricado con un acero de límite elástico "fyb", cumpliéndose además que fy ≤ fyb.
Entonces la resistencia al aplastamiento de la pieza (FA,p) contra el bulón, viene dada por la siguiente expresión:
FA,p = 1,5 · t · d · fy / γM0
donde γM0 es el coeficiente parcial para la resistencia del acero del que está fabricado la pieza situada contra el bulón, cuyo valor para los estados límites últimos es de γM0 = 1,05.
Para que la unión del bulón contra la pieza presente seguridad suficiente al aplastamiento de la pieza, se deberá cumplir por tanto que:
FE,b ≤ FA,p
Siendo FE,b el valor del esfuerzo cortante que actúa sobre el bulón.
Para el caso que el bulón instalado sea desmontable, entonces la resistencia al aplastamiento de la pieza en el estado límite de servicio (FA,p,ser), viene dada por esta otra expresión:
FA,p,ser = 0,6 · t · d · fy
Cumpliéndose en todo caso que:
FE,b,ser ≤ FA,p,ser
3- Ejemplos de cálculo de bulones
3.1- Ejemplo 1: Bulón sometido a esfuerzo cortante
Como ejemplo de cálculo que ilustre cómo calcular un bulón sometido a esfuerzo cortante (con dirección transversal al bulón), se puede considerar el ejemplo de la figura adjunta.
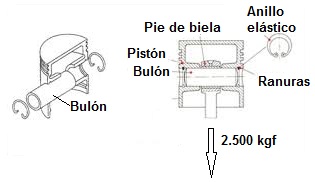
Se trata del bulón empleado en un pistón de un motor de combustión interna que debe resistir el esfuerzo resultante de la presión que origina la combustión de la mezcla de gasolina y aire en el interior del cilindro del motor.
El bulón es la pieza cilíndrica que sirve de unión entre la biela y el pistón, y que permite un cierto giro relativo del eje de la biela con respecto al pistón. Se trata pues de un bulón de tipo flotante.
En este ejemplo se estudiará la idoneidad de emplear un bulón de acero macizo de diámetro d = 20 mm, para resistir con garantías la acción del esfuerzo cortante que transmite el pistón a la biela, esfuerzo que es transversal al bulón, y de valor, para este caso, de 2.500 kgf.
Las características mecánicas del bulón empleado para este caso son las siguientes:
• Diámetro del bulón, d = 20 mm;
• Calidad del acero del bulón:
- Designación: C25
- Tipo de tratamiento: temple y revenido
- Límite elástico, fyb = 320 N/mm2
- Límite último de rotura, fub = 500 N/mm2
Como se ha dicho, el bulón se empleará en la unión entre piezas (pistón y biela), cuya solicitación máxima esperada transversalmente sobre el bulón será en este caso de 2.500 kgf:
FE,b = 2.500 kgf = 24.517 N
Por otro lado, la resistencia a cortante (FR,b) de un bulón viene determinada por la siguiente expresión, según se vio en el apartado 2.2:
FR,b = 0,6 · A · fub / γMb
donde,
A es la sección transversal del bulón, que para el caso de este ejemplo, al tratarse de un bulón de sección cilíndrica con un diámetro de 20 mm vale, A = 314 mm2;
fub es el valor de la resistencia última o límite de rotura del acero del bulón, que en este caso vale, fub = 500 N/mm2;
γMb es el coeficiente parcial para la resistencia del acero del que está fabricado el bulón, que para uniones con bulón, se tiene que γMb = 1,25.
Sustituyendo, la resistencia a cortante (FR,b) del bulón valdrá:
FR,b = 75360 N
Por lo que se cumple que el valor de la fuerza actuante (FE,b) sobre el bulón es inferior a su resistencia a cortante (FR,b):
FE,b = 24.517 N < FR,b = 75.360 N
Por último, el coeficiente de seguridad (λ) obtenido para las condiciones de trabajo del bulón será igual a:
λ = FR,b / FE,b = 75360 / 24517 = 3,07 > 3
Se recomienda, como medida de seguridad estructural, que el coeficiente de seguridad que se obtenga para el trabajo del bulón sea al menos mayor a 3 (λ>3), como efectivamente así se cumple en nuestro ejemplo.
3.2- Ejemplo 2: Bulón sometido a cortante + flector
En este ejemplo se va a estudiar el caso típico de un enganche trasero para vehículo, que incluye un bulón para enganchar con la lanza del remolque. En este caso se comprobará que el bulón utilizado en el enganche es capaz de desarrollar una capacidad máxima de tiro, que incluya el peso del remolque y su carga, de 5.000 kgf (FE,b = 5.000 kgf).
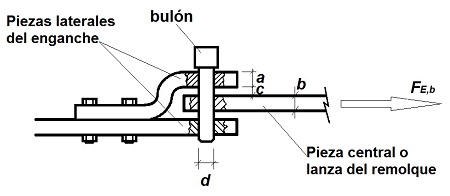
Según se muestra en la figura esquemática adjunta que representa la configuración del enganche, las dimensiones geométricas del enganche y el bulón son las siguientes:
• diámetro del bulón, d = 30 mm;
• espesor de la pieza central (lanza del remolque), b = 35 mm;
• espesores de las piezas laterales del enganche, a = 20 mm;
• separación entre las piezas laterales de la central, c = 15 mm.
La calidad del acero que se ha empleado en la fabricación del bulón para este ejemplo, responde a las siguientes características mecánicas:
• Calidad de acero del bulón:
- Designación: C45
- Tipo de tratamiento: temple y revenido
- Límite elástico, fyb = 430 N/mm2
- Límite último de rotura, fub = 650 N/mm2
Como se ha descrito anteriormente, la solicitación máxima que actuará sobre el bulón del enganche será igual a su capacidad máxima de tiro, que en este caso vale:
FE,b = 5.000 kgf = 49.033 N
Este esfuerzo va a generar en el bulón del enganche, según lo visto en el apartado 2.3, un momento flector (ME,b) cuyo valor se calcula como sigue:
ME,b = FE,b · (b + 4c + 2a)/8
Que sustituyendo los valores de las dimensiones del enganche para este ejemplo, resulta un valor para el momento flector de:
ME,b = 49033 · (35 + 4·15 + 2·20)/8 = 827.432 mm·N
Por lo tanto, ya se han calculado los valores de (FE,b) y (ME,b) que actúan sobre el bulón del enganche.
Ahora, y según lo expuesto en el apartado 2.4 anterior, para los casos donde el bulón de acero esté sometido simultáneamente a la acción combinada de un esfuerzo cortante (FE,b), y de un momento flector (ME,b), se deberá cumplir la siguiente relación, para que la resistencia que ofrezca el bulón sea suficiente:
( ME,b / MR,b )2 + ( FE,b / FR,b )2 ≤ 1
siendo (MR,b) el momento flector resistente y (FR,b) la resistencia a cortante del bulón, que se calculará según las expresiones dadas en los apartados 2.3 y 2.2 anteriores respectivamente.
- Cálculo del valor de resistencia a cortante del bulón del enganche (FR,b):
Según el apartado 2.2, la resistencia a cortante de un bulón viene dado por la siguiente expresión:
FR,b = 0,6 · A · fub / γMb
donde,
A es la sección transversal del bulón, que al tratarse de un bulón de sección cilíndrica de diámetro 30 mm vale, A = 707 mm2
fub es el valor de la resistencia última o límite de rotura del acero del bulón, que en este caso vale, fub = 650 N/mm2
γMb es el coeficiente parcial para la resistencia del acero del bulón, que para uniones con bulones, se tiene que γMb = 1,25.
Sustituyendo los valores anteriores, la resistencia a cortante (FR,b) del bulón del enganche valdrá:
FR,b =220.584 N
- Cálculo del valor de resistencia a flexión del bulón del enganche (MR,b):
Según el apartado 2.3, la resistencia a flexión (MR,b) de un bulón viene dado por la siguiente expresión:
MR,b = 1,5 · W · fyb / γMb
Siendo el módulo resistente (W) de la sección del bulón de giro del que resulta de la siguiente expresión:
|
I |
|
W = |
|
|
|
d / 2 |
|
donde,
I es el momento de inercia de la sección del eje del bulón, de valor I = (π·d4)/64, siendo d el diámetro del bulón.
Sustituyendo el valor del diámetro del bulón, d = 30 mm, resulta un momento de inercia I = 39.761 mm4.
Por lo que el módulo resistente (W) del bulón vale finalmente:
W = 39.761 / (30/2) = 2.651 mm3.
Sustituyendo en la anterior expresión que proporciona la resistencia a flexión (MR,b) del bulón del enganche, ésta resulta ser de:
MR,b = 1,5 · W · fyb / γMb = 1,5 · 2651 · 430 / 1,25 = 1.367.916 mm·N
Ahora sólo queda comprobar que se cumple con la relación indicada en el apartado 2.4:
( ME,b / MR,b )2 + ( FE,b / FR,b )2 ≤ 1
Sustituyendo los valores obtenidos se tiene que:
( 827432 / 1367916 )2 + ( 49033 / 220584 )2 = 0,42 ≤ 1
Por lo que se CUMPLE con la condición indicada, resultando válido el bulón para el enganche con la capacidad de arrastre establecido al principio de este apartado.
>> FIN DEL TUTORIAL
Volver a
Tutoriales
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055
