- Tutorial nº 17 -
Cálculo del Bulón de Giro
en los Vehículos Tipo Volquete
Índice de contenidos:
1- Introducción
1.1- Generalidades
1.2- Consideraciones previas
2- Especificaciones de diseño
2.1- Material
2.2- Esfuerzos sobre el bulón de giro
3- Bulón de giro
3.1- Tensión de trabajo
3.2- Dimensiones
4- Cojinete
4.1- Cálculo de la resistencia
4.2- Dimensiones
5- Ejemplo de cálculo
5.1- Datos de partida
5.2- Esfuerzo sobre el bulón de giro
5.3- Cálculo del bulón de giro
5.4- Diseño del cojinete
DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Generalidades
Este tutorial va a tratar de exponer cómo llevar a cabo el diseño de uno de los componentes del carrozado en los vehículos volquetes: el bulón de giro de la caja basculante.

Los vehículos volquetes, también llamado basculantes, se caracterizan porque su caja de carga puede girar impulsado por uno cilindro hidráulico para poder descargar su carga.
El punto de articulación o eje sobre el cual gira la caja de carga es un elemento sensible y de vital importancia en el diseño de este tipo de carrozado.
En este tutorial se estudiará los componentes que constituyen el eje de articulación sobre el cual voltea la caja de carga de los vehículos volquetes o basculantes: bulón de giro y cojinete.
Por último, al final de este tutorial se incluirá un ejemplo de cálculo que pueda servir de guía para realizar el diseño del bulón de giro y cojinete de un caso concreto de vehículo volquete.
A continuación, se pasa a desarrollar el contenido completo de este tutorial.
1.2- Consideraciones previas
El diseño de las dimensiones del bulón de giro en una caja basculante vendrá determinada, o bien por la resistencia a los esfuerzos cortantes y de flexión del propio bulón, o bien por la resistencia al aplastamiento del material del cojinete donde se aloja.
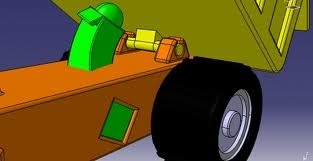
Generalmente, el eje de giro de la caja basculante suele tener dos puntos de apoyos o bulones, como se ve en la figura adjunta, aunque este número puede ser mayor si por las dimensiones o carga máxima de la caja así se requiera.
En todo caso, para este tutorial se va a considerar que la caja de carga dispondrá de dos puntos de apoyo sobre el bastidor del vehículo mediante sendos bulones de giro, los cuales irán alojados en los correspondientes cojinetes de fricción.
El método de diseño que se describa en este tutorial podrá ser válido, no obstante, si el eje de articulación de la caja de carga dispone de más de dos puntos de apoyo, como es el caso de grandes vehículos volquetes.
2- Especificaciones de diseño
2.1- Material
Los bulones de giro para una caja de carga basculante normalmente se fabricarán en acero al carbono F-1140 según se especifica en la normativa UNE (1045 AISI/SAE). La designación numérica para este tipo de acero es 1.1191 y la simbólica C45E, según la normativa EN 10083-1.

Este es un tipo de acero apto para uso general, válido para su empleo en los trabajos de carrozado de vehículos, que ofrece una resistencia media (650-800 N/mm2) en estado bonificado, apto para el temple superficial.
Generalmente para este tipo de piezas se recurre a un proceso de temple superficial, con el fin de dotar al bulón de una mayor dureza superficial y buena resistencia exterior al desgaste, requisitos ambos imprescindible para la función que desempeña los bulones de giro de la caja de carga de un camión.
A continuación, se resumen las características mecánicas del material empleado en la fabricación del bulón de giro para una caja basculante:
• Acero ……....…….………………......………………… F-1140 tratado.
• Tensión de rotura …………………………………. σr = 65-80 kg/mm2.
• Tensión límite de elasticidad …….…...…………….. σe = 35 kg/mm2.
2.2- Esfuerzo sobre el bulón de giro
Para poder dimensionar correctamente el bulón de giro, es necesario conocer las acciones que se ejercen sobre él como consecuencia del peso de la carga que actúa, no sólo cuando la caja de carga del vehículo bascula y está inclinada para descargar la carga, sino también en los instantes iniciales de vuelco de la mercancía, donde la caja se mantiene todavía en posición totalmente horizontal.
Según la figura 4 que se adjunta a continuación, se indica con O1 la posición del punto de articulación de la caja de carga basculante, donde va alojado el bulón de giro, objeto de cálculo de este tutorial.
El esfuerzo que reciba el bulón de giro va a depender directamente del peso de la caja basculante más la mercancía que transporte en su interior. En este sentido se va a denominar Q al peso propio de la caja basculante del vehículo más la carga máxima que pueda transportar, que se considera que actúa en el centro de gravedad de la caja de carga (punto M), al suponerse la carga uniformemente distribuida en su interior.
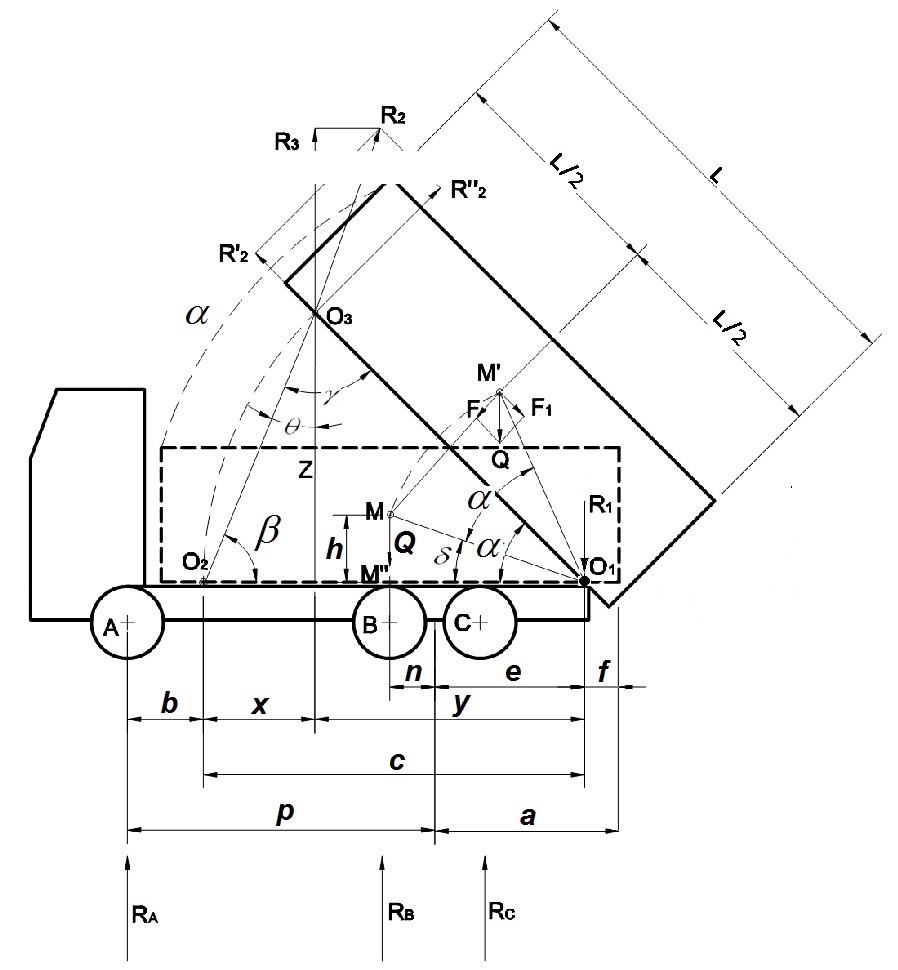
Figura 4. Parámetros geométricos del vehículo carrozado
A continuación se definen los distintos parámetros geométricos que se indican en la figura 4 anterior y que describen la geometría del carrozado del vehículo, algunos de los cuales serán necesarios conocer dado que intervendrán en el cálculo del esfuerzo sobre el eje de articulación de la caja de carga:
• L: es la longitud de la caja de carga basculante.
• a: es el voladizo posterior de la caja de carga.
• p: es la distancia entre los ejes delantero y trasero del vehículo. En caso que el eje trasero se trate de un tándem de dos ejes, se considera el punto medio del tándem.
• O1: es el punto de articulación de la caja de carga basculante.
• O2: es el punto del soporte del cilindro hidráulico elevador.
• O3: es el punto de empuje del cilindro elevador sobre la caja de carga basculante.
• α: representa el ángulo de giro de la caja de carga con respecto al bastidor del vehículo, es decir, el ángulo que bascula la caja.
• δ: es el ángulo con respecto al bastidor que forma la línea que une el punto O1 con el centro de gravedad (c.d.g.) de la carga (punto M).
• β: es el ángulo de inclinación del cilindro elevador con respecto al bastidor.
• c: es la distancia entre los puntos O1 y O2.
• f: es la distancia entre el eje de articulación de la caja de carga basculante y el extremo posterior de ésta.
• e: es la distancia entre el eje trasero y el punto de articulación O1 de la caja.
• b: es la distancia entre el eje delantero y el punto de soporte del cilindro elevador O2.
• R1: es el esfuerzo que actúa sobre el eje de articulación de la caja de carga.
• R2: es el esfuerzo sobre la caja de carga debido al empuje del cilindro elevador.
• R3: es la componente perpendicular al bastidor del vehículo del esfuerzo de empuje del cilindro elevador.
• Q: es el peso de la caja de carga basculante más su carga máxima que pueda transportar.
Para conocer las acciones que se ejercen sobre el eje de articulación sobre el cual bascula la caja de carga, se estudiarán dos casos: en posición horizontal de la caja (ángulo de inclinación, α = 0º) y en posición de vuelco con la caja inclinada un ángulo (α), debiéndose seleccionar para el cálculo del bulón el mayor de los valores obtenidos.
A) En posición de inicio de vuelco de la mercancía, α=0º
En el comienzo de elevación de la caja de carga (α=0º), el bulón de giro de la caja comienza a estar sometido a una carga puntual (R1(α=0)) como consecuencia del empuje que sobre la caja se ejerce por parte del cilindro hidráulico elevador (R3(α=0)).
Aplicando las ecuaciones de equilibrio de momentos con respecto al punto O2 de las fuerzas actuantes R1(α=0) y Q (ver figura 4 anterior) se obtiene la siguiente igualdad entre los momentos de fuerzas:
R1(α=0) · c = Q · [c - (L/2-f)]
Y despejando se puede obtener la expresión que proporciona el valor de la reacción que se ejerce sobre el bulón de giro en el comienzo de elevación de la caja de carga (R1(α=0)):
|
Q · [c - (L/2-f)] |
|
R1(α=0) = |
——————— |
|
|
c |
|
B) En posición de vuelco (α) de la caja de carga
De la misma manera que en el caso anterior, se aplicaría las condiciones de equilibrio de momentos para la situación donde la caja de carga se encuentra inclinada un ángulo (α) respecto a la horizontal.
Esta es una situación típica donde la caja de carga está basculando para descargar la mercancía que se encuentra en el interior de la caja.
En este caso, aplicando las ecuaciones de equilibrio de momentos con respecto al punto O3 de las fuerzas actuantes R1(α) y Q (ver figura 4 anterior) se obtendría la siguiente expresión que proporcionaría la reacción sobre el bulón de giro de la caja de carga cuando ésta está inclinada un ángulo (α):
R1(α) = Q · [1 - (L/2-f)/c · (cos(α+δ)/cosδ)]
Siendo δ el ángulo que forma con respecto al bastidor del vehículo la línea que une el punto O1 (eje de articulación de la caja) con el c.d.g. de la carga (punto M).
Dicho ángulo (δ) cumple con la siguiente relación geométrica, según la figura 4 anterior:
tgδ=h/(L/2-f), donde h es la altura del c.d.g. de la caja de carga respecto al bastidor del vehículo.
Una vez estudiadas las dos situaciones anteriores, finalmente se empleará como valor de diseño para el esfuerzo actuante (R1) sobre el eje de articulación de la caja el mayor valor obtenido de los anteriores (R1(α=0) ó R1(α)).
3- Bulón de giro
3.1- Tensión de trabajo
Según el apartado anterior, R1 es el esfuerzo que actúa sobre el eje de articulación o giro de la caja de carga, y por lo tanto, su diseño se realizará de tal forma que pueda soportar sin problemas este esfuerzo R1.
Como ya se dijo anteriormente, la caja de carga basculante cuenta con dos apoyos constituidos por sendos bulones para el eje de articulación, por lo que cada bulón recibirá la mitad de la carga (R1/2) transmitida al eje de articulación.
La carga debida al peso de la caja y su mercancía, y que se transmite a cada bulón de giro (de valor R1/2), producirá en el propio bulón un esfuerzo cortante o esfuerzo de cortadura (V), además de un momento flector (Mf), que darán lugar a su vez a las respectivas tensiones de cortadura y normales por flexión en la sección del bulón.
A continuación se expondrá cómo calcular dichas tensiones, que son necesarias conocer para proceder al diseño adecuado del bulón de giro.
Se adjunta, para una mayor comprensión por parte del lector, de una figura explicativa del proceso de la transmisión de cargas que se produce sobre el eje de articulación de la caja y los bulones de giro:
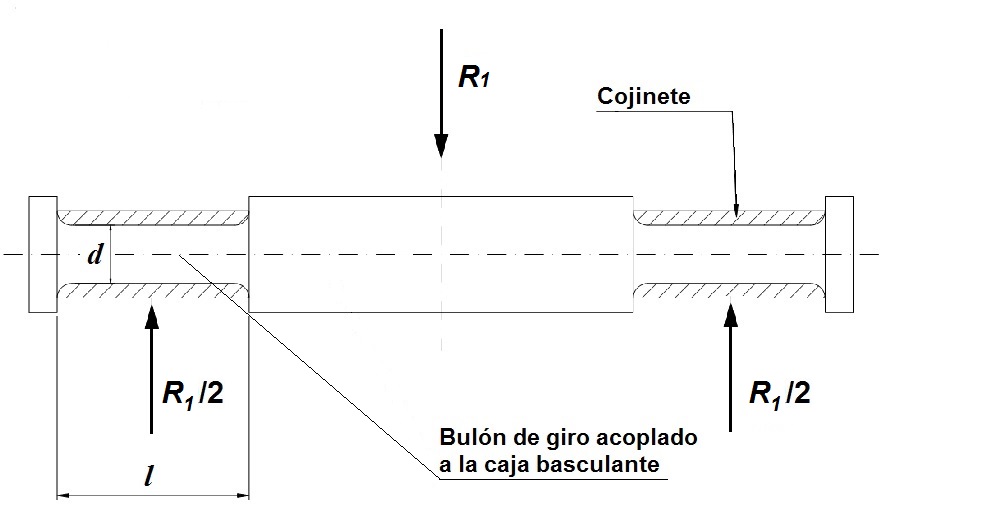
Figura 6. Transmisión de cargas al bulón
- Tensión a cortadura:
Como ya se ha dicho, la carga transmitida (R1) producirá en cada apoyo un esfuerzo de tipo cortante o esfuerzo de cortadura (V) en la sección del bulón de giro igual a la carga que soporta cada apoyo, esto es V=R1/2.
El esfuerzo cortante (V) a su vez genera una tensión de cortadura (τ) en la sección del bulón, de valor:
|
V |
|
τ = |
——— |
|
|
Av |
|
siendo V el esfuerzo cortante sobre el bulón (en este caso, V=R1/2) y Av es el área de la pieza que interviene a resistencia en el cortante. En esta ocasión, coincide con el área de la sección cilíndrica del bulón (Av = π·d2/4)
Por otro lado, según el criterio de Von-Mises, la tensión cortante límite (τlím) cuando se alcanza el límite elástico de la pieza vale:
|
σe |
|
τlím = |
——— |
|
|
√3 |
|
Combinando las dos anteriores expresiones se obtendrá la resistencia plástica de la sección del bulón a cortadura (Vmáx), cuando éste alcanza su límite elástico:
|
σe |
|
Vmáx = Av · |
——— |
|
|
√3 |
|
siendo, Av = π·d2/4, y el límite elástico del material del bulón, σe = 35 kg/mm2, para acero F-1140, según se vio en el apartado 2.1.
Vmáx representa el esfuerzo cortante máximo que puede soportar cada apoyo antes de llegar a su límite elástico.
Como comprobación a resistencia plástica de la sección del bulón a cortadura, se deberá comprobar por tanto que se cumple la siguiente condición:
Vmáx > γ · V
donde, V es el esfuerzo cortante al que está sometido el bulón (V=R1/2), mientras que "γ" es un coeficiente de seguridad. Como este tipo de articulación es de gran responsabilidad se aconseja exigir un coeficiente de seguridad, γ=3.
- Tensión normal por flexión:
Por otro lado, el esfuerzo que actúa en cada apoyo del bulón (R1/2) genera también un momento flector (Mfmáx), que será máximo en el extremo del eje del bulón y cuyo valor vendrá dado por la siguiente expresión:
|
R1 · l |
|
Mfmáx = (R1/2)·(l/2) = |
——— |
|
|
4 |
|
Siendo (l) la longitud del bulón de giro.
Este momento flector crea una tensión normal en la sección del bulón (σf) por flexión, cuyo valor máximo viene dado por la siguiente ecuación de resistencia:
|
Mfmáx |
|
σf = |
——— |
|
|
Wx |
|
donde,
σf es la tensión de trabajo normal en la sección del bulón por flexión.
Mfmáx es el momento flector máximo que actúa sobre la sección del bulón, según la expresión anterior.
Wx es el módulo resistente a flexión de la sección del bulón según el eje de flexión.
El módulo resistente (Wx) de la sección del bulón de giro, que es una pieza cilíndrica, viene dada por la siguiente expresión:
|
Ixx |
|
Wx = |
——— |
|
|
d / 2 |
|
donde,
Ixx es el momento de inercia de la sección del eje, de valor Ixx = (π·d4)/64, siendo d el diámetro del bulón.
Por lo que el módulo resistente (Wx) vale,
|
π · d3 |
|
Wx = |
——— |
|
|
32 |
|
Y la tensión (σf) a la que trabaja el bulón se podrá expresar como,
|
32 · Mfmáx |
|
σf = |
————— |
|
|
π · d3 |
|
3.2- Dimensiones
En este apartado se tratará de ver cómo se calcula las dimensiones del diámetro (d) y la longitud) (l) que ha de tener el bulón de giro de la caja basculante, para que su diseño resulte óptimo y la vez seguro.
De la expresión última del apartado anterior, donde se obtiene la tensión de trabajo (σf) del bulón de giro en función del esfuerzo máximo de flexión (Mfmáx) a la que está sometido, se puede despejar el valor del diámetro (d) del bulón, resultando:
|
32 · Mfmáx |
|
d = ( |
——————)1/3 |
|
|
σf · π |
|
Y por otro lado, como el momento flector máximo (Mfmáx), ya visto en el apartado anterior, resultaba ser:
|
R1 · l |
|
Mfmáx = (R1/2)·(l/2) = |
——— |
|
|
4 |
|
Sustituyendo el momento flector máximo (Mfmáx), la expresión para el cálculo del diámetro (d) del bulón de giro quedaría como sigue:
|
8 · R1 · l |
|
d = ( |
——————)1/3 |
|
|
σf · π |
|
En la anterior expresión interviene la longitud (l) del bulón de giro, cuyo valor vendrá condicionado por el cojinete donde irá alojado.
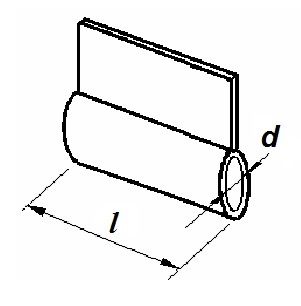
En efecto, las dimensiones finales del bulón (diámetro d, y longitud l) estarán condicionadas por la resistencia que ofrezca el cojinete al aplastamiento.
Ello es así porque las paredes interiores del cojinete van a estar comprimidas al tener que soportar la reacción que transmite el bulón de giro de la caja.
Por otro lado, los cojinetes estarán fabricado generalmente de bronce, un material más blando que el material del que está hecho el bulón (acero tratado).
Por lo tanto, las dimensiones finales del bulón serán tales que la presión que transmita al cojinete no llegue a superar la presión límite de aplastamiento del material.
La presión (p) ejercida sobre las paredes interiores del cojinete por parte del bulón de giro, viene dada por la siguiente expresión:
|
R1 / 2 |
|
p = |
——— |
|
|
Ap |
|
donde, Ap es el valor de la superficie proyectada del cojinete de bronce sobre el eje del bulón, de valor Ap = l·d.
Sustituido en la expresión anterior, la presión (p) que el bulón de giro ejerce sobre las paredes del cojinete quedaría como sigue:
|
R1 / 2 |
|
p = |
——— |
|
|
l · d |
|
Si llamamos plím a la presión máxima por aplastamiento que aguanta el material del cojinete, entonces se deberá cumplir que:
p < plím
O lo que es lo mismo, que:
|
R1 |
|
l > |
—————— |
|
|
2 · plím · d |
|
Condición que debe cumplir la longitud (l) del bulón de giro para que no produzca el aplastamiento del cojinete.
Por otro lado, según se vio anteriormente el valor para el diámetro (d) del bulón de giro se calculaba como:
|
8 · R1 · l |
|
d = ( |
——————)1/3 |
|
|
σf · π |
|
O lo que es lo mismo,
|
8 · R1 · l |
|
d3 = |
———— |
|
|
σf · π |
|
Y por otro lado, como la reacción R1 que transmite el bulón de giro al cojinete viene relacionada con la presión (p) de aplastamiento, a través de la expresión ya vista de:
R1 = 2·p·l·d
El diámetro del bulón también se puede expresar como:
|
8 · 2 · p · l · d · l |
|
d3 = |
——————— |
|
|
σf · π |
|
es decir,
|
16 · p · l2 |
|
d2 = |
————— |
|
|
σf · π |
|
Finalmente, imponiendo la condición p < plím, es decir, que la presión que ejerza el bulón sobre las paredes del cojinete no llegue a ocasionar su fallo por aplastamiento, el diámetro mínimo que deberá tener el bulón de giro deberá cumplir con la siguiente condición:
d > 1,58 · √ [ (R1/σf) · √(0,2·σf/plím) ]
En otro orden de cosas, la dimensión final del diámetro del bulón también vendrá condicionada por la deformación o flecha máxima (fmáx) que se le permita tener, y que sea compatible con un funcionamiento seguro y fiable de la articulación.
En efecto, la reacción (R1) que actúa sobre el bulón genera, como se ha visto, un esfuerzo de flexión (Mf) que lleva aparejado además una deformación de la geometría inicial del bulón. Limitar la deformación máxima que pueda soportar el bulón es vital para que pueda seguir trabajando en condiciones óptimas.
En general, y como buena práctica se considera limitar la flecha máxima que experimenta el eje de giro de la caja basculante en sus articulaciones inferior a 0,08 mm (fmáx ≤ 0,08 mm), requisito que se considera imprescindible para que los cojinetes trabajen en buenas condiciones.
La expresión que proporciona el diámetro mínimo que ha de tener el bulón de giro para que no se supere la condición de flecha máxima en sus articulaciones, viene dado por la siguiente expresión:
d > 4√ [ (0,424·R1·l3) / (2,2·104·fmáx) ]
siendo l la longitud del bulón y fmáx=0,08 mm (la flecha máxima permitida del eje de articulación, según la recomendación dada).
En resumen, y como conclusión, el diámetro mínimo para el bulón de giro (d) se tomará superior al mayor valor que se haya obtenido de las dos anteriores restricciones, esto es:
• por aplastamiento de las paredes del cojinete ;
• por deformación máxima permitida del bulón.
4- Cojinete
4.1- Cálculo de la resistencia
El cálculo de la resistencia a compresión que puede ofrecer el cojinete en el eje de articulación de la caja de carga es de vital importancia, dado que este valor va a condicionar las dimensiones finales que debe tener el bulón de giro que se aloje en el propio cojinete.

En efecto, el bulón de giro de la caja basculante irá alojado en el interior de un cojinete cilíndrico o casquillo, que estará fabricado de un material más blando que el acero del eje, y que por lo tanto absorberá todo el desgaste producido por el bulón durante el movimiento basculante de la caja de carga del vehículo.
De esta forma, como todo el desgaste se producirá en la pieza del cojinete, sólo habrá que reemplazar el propio cojinete una vez se haya desgastado su espesor, resguardando el bulón y el resto de componentes de cualquier desperfecto derivado del uso.
Generalmente, como material de fabricación para el cojinete se empleará el bronce.
En esta ocasión, se ha empleado como cojinete un casquillo de aleación de bronce ASTM B-438 Grado 1 Clase A Tipo II (equivalente AENOR UNE 37.103), de tipo autolubricado, donde alrededor del 20 al 30% del volumen del cojinete está impregnado en aceite, lo que crea una película de aceite permanente que elimina el riesgo de gripado y le confiere un bajo coeficiente de rozamiento.
Para determinar la resistencia radial a la compresión del cojinete (Rc), se puede emplear la siguiente expresión:
|
L · e2 |
|
Rc = Kc · |
————— |
|
|
dext - e |
|
siendo,
Kc la constante de resistencia del material del cojinete, en este caso, 178 N/mm2 para aleación de bronce ASTM B-438.
L es la longitud del cojinete, en mm.
e es el espesor de la pared del cojinete, en mm.
dext es el diámetro exterior del cojinete, en mm.
Calculada la resistencia a la compresión (Rc) que ofrece el cojinete, se deberá comprobar que ésta es superior al valor de la reacción que transmite el bulón de giro al propio cojinete (Rc > R1/2).
Debido a la gran responsabilidad que tiene este tipo de articulación es preciso que trabaje con un coeficiente de seguridad CS no inferior a 3, por lo que se deberá cumplir la siguiente relación:
|
Rc |
|
CS = |
——— > 3 |
|
|
R1 / 2 |
|
4.2- Dimensiones
Como se ha visto anteriormente, las dimensiones (espesor, diámetro y longitud) que debe tener el cojinete que se instale deben ser tales que permita ofrecer una resistencia a la compresión (Rc) que sea suficiente como para soportar la reacción que transmite el eje de la articulación durante el vuelco de la caja de carga, según se ha indicado en el apartado anterior.
Como buena práctica se aconseja que el espesor (e) del casquillo del cojinete que se instale se aproxime, siempre por encima, al valor siguiente:
e = 1/16 · d + 0,5 cm
siendo d el valor del diámetro del hueco cojinete.
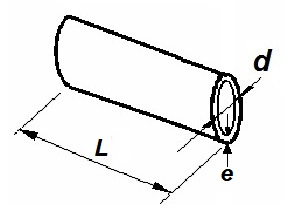
Figura 9. Dimensiones de un cojinete
Por otro lado, para la longitud (L) del cojinete se recomienda que se encuentre dentro del siguiente rango:
1,3 · d < L < 1,8 · d
5- Ejemplo de cálculo
5.1- Datos de partida
Como ejemplo de cálculo, se va a realizar el diseño del bulón de giro (representado en la figura adjunta como O1: punto de articulación de la caja de carga) de un vehículo dotado de caja basculante, cuyas características y dimensiones se exponen a continuación:

• Longitud de la caja de carga, L= 3050 mm.
• Voladizo posterior de la caja de carga, a= 1300 mm.
• Distancia entre los ejes delantero y trasero del vehículo, p= 2400 mm.
• Distancia entre los puntos O1 (punto de articulación de la caja de carga) y O2 (punto del soporte del cilindro hidráulico elevador de la caja), c= 1250 mm.
• Distancia entre el eje de articulación de la caja de carga y el extremo posterior de ésta, f= 500 mm.
• Distancia entre el eje trasero del vehículo y el punto de articulación O1 de la caja, e= 800 mm.
• Altura del c.d.g. de la caja de carga respecto al bastidor del vehículo, h = 900 mm.
• Distancia entre el eje delantero del vehículo y el punto de soporte del cilindro elevador O2, b= 1950 mm.
• R1: es el esfuerzo que actúa sobre el eje de articulación de la caja de carga (a calcular).
• Peso máximo permitido de la mercancía a transportar por la caja de carga del vehículo, donde está incluido también el peso propio de la caja, Q= 3000 kg.
5.2- Esfuerzo sobre el bulón de giro
El primer paso es calcular la máxima reacción (R1) que debe soportar el eje de articulación de la caja de carga cuando ésta bascule.
Como se vio en el apartado 2.2, para conocer el máximo valor que puede alcanzar la reacción (R1) sobre el eje de giro se estudiarán dos casos:
- en posición horizontal de la caja (ángulo de inclinación, α=0º);
- y en posición de vuelco de la mercancía con la caja inclinada un ángulo (α).
Debiéndose seleccionar para el cálculo del bulón el mayor de los valores que se obtenga.
A) En posición de inicio de vuelco de la mercancía, α=0º
Para el comienzo de elevación de la caja de carga (α=0º), la expresión que proporciona la reacción (R1(α=0)), según se vio en el apartado 2.2, era la siguiente:
|
Q · [c - (L/2-f)] |
|
R1(α=0) = |
——————— |
|
|
c |
|
Que sustituyendo por los valores indicados en el anterior apartado 5.1 "Datos de partida", quedará la expresión como sigue:
|
3000 · [1250 - (3050/2-500)] |
|
R1(α=0) = |
————————————— |
|
|
1250 |
|
Resultando finalmente una reacción sobre el eje de articulación en el comienzo de elevación de la caja de carga de:
R1(α=0) = 540 kg
B) En posición de vuelco un ángulo (α) de la caja de carga
Para la posición de vuelco de la caja de carga con la mercancía, se tomará la posición más desfavorable, que coincide con la de máxima inclinación de la caja (α=45º)
Según el apartado 2.2, la expresión que sirve para calcular la reacción (R1(α)) sobre el eje de giro cuando la caja se encuentra inclinada un ángulo (α), resultaba ser:
R1(α) = Q · [1 - (L/2-f)/c · (cos(α+δ)/cosδ)]
Siendo en esta caso, el ángulo de inclinación de la caja, α=45º.
Por otro lado, el ángulo δ, según se vio en el apartado 2.2, cumplía con la siguiente relación geométrica:
tgδ=h/(L/2-f), donde h era la altura del c.d.g. de la caja de carga respecto al bastidor del vehículo.
Sustituyendo los valores indicados en el apartado 5.1, resulta que:
tgδ=900/[(3050/2)-500]= 0,88
resultando, δ=41º
Conocidos los ángulos (α=45º ; δ=41º) y sustituyendo los valores de los parámetros indicados en el apartado 5.1, la expresión que calcula la reacción (R1(α=45º)) con la caja inclinada un ángulo de 45º, vale:
R1(α=45º) = 3000 · [1 - (3050/2-500)/1250 · (cos(45+41)/cos41)]
Resultando, finalmente:
R1(α=45º) = 2773 kg
Como valor de diseño para dimensionar el bulón de giro se tomará el mayor de los valores obtenidos para la reacción sobre el eje de articulación, resultando:
R1 = 2773 kg
5.3- Cálculo del bulón de giro
Como ya se vio en el apartado 3.2, las dimensiones que deberá tener el bulón de acero que funciona como eje de giro para el volteo de la caja de carga, viene determinado por las siguientes restricciones:
• Por aplastamiento de las paredes del cojinete.
• Por deformación máxima permitida del bulón.
De aplicar cada una de las anteriores restricciones se obtendrá una dimensión mínima para el diámetro del bulón, debiéndose tomar el valor más restrictivo.
Por último, habrá que realizar una definitiva comprobación del estado tensional del bulón, verificando que se encuentra por debajo de su límite elástico.
A) Por aplastamiento de las paredes del cojinete:
Para evitar que se ocasione el fallo en la articulación de la caja por aplastamiento del cojinete, el diámetro del bulón de giro deberá cumplir la siguiente condición, vista en el apartado 3.2:
d > 1,58 · √ [ (R1/σf) · √(0,2·σf/plím) ]
donde,
R1 es el esfuerzo máximo que se espera que actúe sobre el eje de articulación de la caja de carga, en este caso, R1 =2773 kg.
plím es la presión máxima por aplastamiento que aguanta el material del cojinete, en este caso y según el cojinete seleccionado, plím = 18,2 kg/mm2.
σf es el valor máximo admisible que puede alcanzar la tensión de trabajo del bulón, según se define a continuación.
Para poder estimar el valor máximo admisible que puede alcanzar la tensión en el bulón de giro, se tendrá en cuenta la gran responsabilidad que tiene este tipo de articulación.
Por ello, es preciso que esta pieza trabaje con un coeficiente de seguridad (Cs) holgado, por ejemplo, no inferior a 3, tomando como base la tensión límite de elasticidad del material del que está hecho el bulón. Es decir:
Cs = σe/σf = 3, de donde se obtiene el valor máximo admisible para σf.
En este caso, el bulón de la caja estará fabricado con acero F1140, que tiene un límite elástico σe = 35 kg/mm2.
Por lo tanto, el valor máximo admisible de la tensión a la que puede trabajar el bulón de giro será:
σf = σe/3 = 11,67 kg/mm2
Sustituyendo todos estos valores en la expresión primera, resulta un valor mínimo para el diámetro del bulón de:
d > 1,58 · √ [ (2773/11,67) · √(0,2·11,67/18,2) ] = 14,57 mm.
B) Por deformación máxima del bulón:
Según ya se vio en el apartado 3.2, la expresión que proporciona el diámetro mínimo del bulón de giro bajo la condición de flecha máxima en sus articulaciones, era la siguiente:
d > 4√ [ (0,424·R1·l3) / (2,2·104·fmáx) ]
siendo fmáx=0,08 mm la flecha máxima permitida del eje de articulación de la caja, y la longitud (l) del bulón que, según la buena práctica, se recomienda que quede comprendida dentro del siguiente rango, en función del diámetro:
1,3 · d < l < 1,8 · d
Se tomará como longitud inicial del bulón l=35 mm., que habrá que comprobar una vez realizados los cálculos y seleccionado el diámetro final del bulón, para que quede dentro del rango anterior.
Sustituyendo los valores en la expresión anterior, se obtendrá el diámetro mínimo del bulón bajo la condición de limitar su deformación máxima:
d > 4√ [ (0,424·2773·353) / (2,2·104·0,08) ] = 13,01 mm.
Finalmente, se optará por colocar un bulón de giro de las siguientes características:
• Material: Acero F-1140.
• Diámetro (d): 25 mm.
• Longitud (l): 35 mm.
Que cumple holgadamente con las condiciones anteriores.
C) Comprobación del estado tensional del bulón:
Por último habrá que comprobar que el estado de tensiones al que esté trabajando el bulón no supere su límite elástico.
- Tensión de cortadura:
El esfuerzo cortante (V) que actúa sobre el bulón de giro genera una tensión de cortadura (τ) en la sección del bulón, de valor:
|
V |
|
τ = |
——— |
|
|
Av |
|
siendo,
V el esfuerzo cortante que actúa sobre el bulón de giro, que en este caso vale, V = R1/2 = 2773/2 = 1386,5 kg.
Av es el área de la sección cilíndrica del bulón, de valor Av = π·d2/4 = π·252/4 = 490,87 mm2.
Por lo que, la tensión de cortadura (τ) en la sección del bulón, resulta:
|
1386,5 |
|
τ = |
———— = 2,82 kg/mm2. |
|
|
490,87 |
|
Como se sabe, según el criterio de Von-Mises, la tensión cortante (τlím) en el límite elástico de la pieza vale:
|
σe |
|
τlím = |
——— |
|
|
√3 |
|
donde el límite elástico (σe) del material del bulón, acero F-1140, vale σe = 35 kg/mm2, según se vio en el apartado 2.1.
Por lo que finalmente la tensión límite de cortadura en el límite elástico valdrá:
|
35 |
|
τlím = |
——— = 20,21 kg/mm2. |
|
|
√3 |
|
Comprobándose que el bulón trabaja a cortadura por debajo de su límite elástico, dado que:
τ = 2,82 kg/mm2 < τlím = 20,21 kg/mm2.
Resultando un coeficiente (γV) de seguridad por tensión de cortadura de:
γV = τlím / τ = 20,21 / 2,82 = 7,2
- Tensión a flexión:
Como ya se vio en el apartado 3.1, el esfuerzo que actúa en cada apoyo del bulón (R1/2) genera también un momento flector (Mfmáx), que será máximo en el extremo del eje del bulón y cuyo valor viene dado por la siguiente expresión:
|
R1 · l |
|
Mfmáx = (R1/2)·(l/2) = |
——— |
|
|
4 |
|
Siendo (l) la longitud del bulón de giro, en este caso de valor, l = 35 mm.
Sustituyendo los correspondientes valores, se obtiene un momento flector máximo de:
|
2773 · 35 |
|
Mfmáx = |
————— = 24264 kg·mm. |
|
|
4 |
|
Por otro lado, ya se vio en el apartado 3.1, que la tensión normal por flexión (σf) también se puede expresar como:
|
32 · Mfmáx |
|
σf = |
————— |
|
|
π · d3 |
|
que sustituyendo valores se obtiene:
|
32 · 24264 |
|
σf = |
————— = 15,82 kg/mm2. |
|
|
π · 253 |
|
Tensión que es inferior al límite elástico (σe) del material del bulón, que vale σe = 35 kg/mm2, según se vio en el apartado 2.1.
Y por lo tanto, el coeficiente de seguridad (γf) por flexión resultará de:
γf = σe / σf = 35 / 15,82 = 2,2
- Tensión de comparación:
Por último, se empleará el criterio de dimensionamiento de Von-Mises para comprobar que la tensión máxima que se alcance en cualquier sección del bulón de giro sea inferior a su límite elástico.
Para ello se emplea la tensión de comparación (σco) que combina la acción conjunta de ambas tensiones, normal (σ) y cortante (τ), para compararla con el límite elástico del material.
La expresión que calcula la tensión de comparación (σco) es la siguiente:
σco = √(σ2+3·τ2)
Por lo que el cumplimiento del anterior criterio exige que:
σco = √(σ2+3·τ2) ≤ σe
Sustituyendo los valores de las tensiones anteriormente calculadas se tiene la siguiente tensión de comparación (σco):
σco = √(σ2+3·τ2) = √(15,822+3·2,822) = 16,56 kg/mm2.
Que resulta inferior al límite elástico del material (σe), de valor σe = 35 kg/mm2:
σco ≤ σe
16,56 kg/mm2 ≤ 35 kg/mm2
5.4- Diseño del cojinete
Como ya se vio en el capítulo 4 de este tutorial, se empleará un cojinete cilíndrico de bronce sinterizado ASTM B-438 Grado 1 Clase A Tipo II (equivalente AENOR UNE 37.103), de tipo autolubricado, donde del 20 al 30% del volumen del cojinete está impregnado en aceite, lo que crea una película de aceite permanente que elimina el riesgo de gripado y le confiere un bajo coeficiente de rozamiento.
Como una primera aproximación, el espesor (e) del casquillo del cojinete que se instale será, como mínimo, el que resulte de la expresión siguiente:
e = 1/16 · d + 0,5 cm
siendo d el diámetro del bulón que se aloja en su interior, en este caso, d = 25 mm.
Sustituyendo resulta un espesor de pared mínimo, e = 6,56 mm.
Por otro lado, para la longitud (L) del cojinete se recomienda que se encuentren dentro del siguiente rango:
1,3 · d < L < 1,8 · d
resultando,
32,5 mm < L < 45 mm
Finalmente, se elegirá un cojinete que responde a las siguientes características:
• Cojinete de bronce ASTM B-438 autolubricado, tipo cilíndrico.
• Diámetro interior, dint = 25 mm.
• Diámetro exterior, dext = 49 mm.
• Espesor de pared del casquillo, e = 12 mm.
• Longitud, L= 35 mm.
Cojinete, cuya denominación comercial será: Tipo A-25-49-35.
Por último, habrá que comprobar que la resistencia radial del cojinete (Rc) seleccionado sea suficiente como para soportar la reacción que va a transmitir el bulón de giro en cada apoyo (R1/2). Es decir, se tiene que cumplir que:
Rc > R1/2
Para determinar la resistencia radial a la compresión del cojinete (Rc) se empleará la siguiente expresión:
|
L · e2 |
|
Rc = Kc · |
————— |
|
|
dext - e |
|
siendo,
Kc la constante de resistencia del material del cojinete, en este caso, 178 N/mm2 para aleación de bronce ASTM B-438.
L es la longitud del cojinete, de valor L= 35 mm.
e es el espesor de la pared del cojinete, de valor e = 12 mm.
dext es el diámetro exterior del cojinete, de valor dext = 49 mm.
Sustituyendo, resulta una resistencia a la compresión del cojinete de:
Rc = 24246 N (2474 kg.)
Por otro lado, la reacción que transmite el bulón de giro en cada apoyo vale:
R1/2 = 2773/2 = 1386,5 kg.
Valor que es inferior a la resistencia a la compresión que ofrece el cojinete seleccionado.
>> FIN DEL TUTORIAL
Volver a
Tutoriales
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055
