— Leyes y Fórmulas Matemáticas —
Sistemas de Medida de Ángulos
Tabla de contenidos:
1.- Sistemas de medida de ángulos
1.1- Radianes
1.2- Sistema sexagesimal
1.3- Sistema centesimal
1.4- Milésima artillera
2.- Métodos de conversión entre los sistemas de medida de ángulo
2.1- Pasar de radianes a grados sexagesimales
2.2- Pasar de radianes a grados centesimales
2.3- Pasar de grados sexagesimales a radianes
2.4- Pasar de grados sexagesimales a grados centesimales
2.5- Pasar de grados centesimales a grados sexagesimales
2.6- Pasar milésimas artilleras a grados sexagesimales
2.7- Pasar milésimas artilleras a grados centesimales
2.8- Pasar de porcentaje en tanto por ciento a ángulo sexagesimal
DESARROLLO DEL CONTENIDO
1- Sistemas de medida de ángulos
1.1- Radianes
Un radián es la unidad de medida de un ángulo con vértice en el centro de una circunferencia y cuyos lados delimitan un arco de circunferencia que tiene la misma longitud que el radio. El radián (rad) es la unidad de medida para ángulos en el Sistema Internacional de Unidades (S.I.).
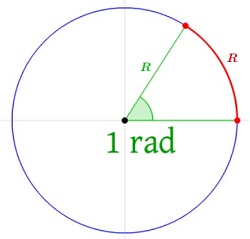
La relación del radián con la otra unidad de medida para ángulos más ampliamente utilizada, los grados sexagesimales o simplemente grados (º), es la siguiente:
1 vuelta completa de la circunferencia = 360º = 2 · π radianes
Para entender la anterior igualdad, se parte de saber que la medida en radianes de un ángulo (θ) medido en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia, es decir:
|
Longitud del arco |
|
θ(radianes) = |
|
|
|
Radio |
|
Por tanto, cuando se trata del ángulo correspondiente a una circunferencia completa, cuya longitud total es 2·π·r (siendo r el radio de la circunferencia) le corresponden en radianes un ángulo de:
|
2·π·r |
|
θ(circunferencia completa) = |
= 2·π radianes |
|
|
r |
|
En el sistema sexagesimal, el ángulo que abarca la circunferencia completa mide 360º, por lo que se puede establecer la ya vista relación entre grados y radianes:
1 vuelta completa = 360º = 2 · π radianes
Otras equivalencias útiles entre grados y radianes son las siguientes:
0º = 0 rad
90º = π/2 rad
180º = π rad
1.2- Sistema sexagesimal
El sistema sexagesimal es un sistema de unidades muy empleado cuyo fundamento es que cada unidad se divide en 60 unidades de una orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad fundamentalmente para la medida de ángulos y también en la medida del tiempo.
La unidad de medida de ángulos en el sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales, o bien un ángulo recto en 90 partes, o un ángulo completo en 360 partes. A cada una de esas partes se les llama grado (º). Así, un ángulo llano mide 180º, un ángulo recto 90º y un ángulo completo 360º.
A su vez, cada grado se subdivide en otras unidades inferiores, en concreto, en sesenta partes iguales. De esta manera, cada grado se divide en 60 minutos (1º = 60´) y cada minuto, a su vez, en 60 segundos (1´ = 60´´).
• Medidas de ángulos: 1 grado (º) → 60 minutos (´) → 60 segundos (´´)
• Medidas de tiempo: 1 hora → 60 minutos (´) → 60 segundos (´´)
Por tanto, en general, un ángulo en el sistema sexagesimal vendrá expresado en grados, minutos y segundos, de la forma, por ejemplo: 38º 50´ 35´´ (38 grados, 50 minutos y 35 segundos). Si se omiten los minutos y segundos, por ejemplo, 45º, es porque se entiende que es 45º 0´ 0´´.
Cuando un ángulo se mide en grados, minutos y segundos, se dice que está expresado con medida compleja, mientras que si se expresa con una sola clase de unidades, se dice que es una medida incompleja o simple, por ejemplo:
32º → medida simple
11´´ → medida simple
52º 17´ 45´´ → medida compleja
4º 22´ → medida compleja
Para sumar grados expresados en medidas complejas, primero se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos, y se suman, como se indica en el siguiente ejemplo de la figura:
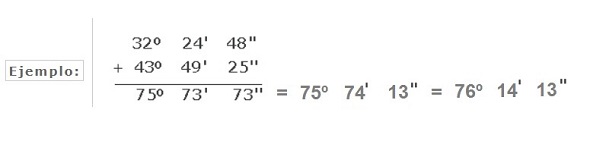
Como se ve en el ejemplo anterior, si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirá a los minutos. Se hace lo mismo para los minutos, si estos resultasen también una cantidad mayor de 60.
A continuación, se incluye un PDF con más ejercicios resueltos de suma, resta y divisiones de ángulos expresados en grados, minutos y segundos.
›› Operaciones de ángulos expresados en grados, minutos y segundos
- Paso de una medida compleja a incompleja:
Para pasar de medidas complejas a incomplejas hay que transformar cada una de las unidades que tenemos en la que queremos obtener y posteriormente sumarlas, por ejemplo:
Pasar de la forma compleja 2º 25´ 30´´ a un simple en segundos:
1º) Se pasan los 2º a minutos: 2·60 = 120 minutos, y posteriormente a segundos: 120·60 = 7200 segundos
2º) Se pasan los 25 minutos a segundos: 25·60 = 1500 segundos
3º) Se suman todos los segundos: 7200´´ + 1500´´ + 30´´ = 8730 ´´
Por tanto, 2º 25´ 30´´ = 8730 segundos
- Pasar de unidades incomplejas a complejas:
Para pasar una medida expresada en unidades incomplejas a complejas, habrá que dividir cuando el caso sea de pasar a unidades de orden superior, o multiplicar para pasar a unidades de orden inferior, por ejemplo:

1.3- Sistema centesimal
El sistema centesimal divide una circunferencia en 400 partes iguales, o bien, un ángulo recto en 100 partes iguales, y a cada una de esas partes se le denomina grado centesimal o gradián, y se simboliza con una «g» minúscula como superíndice del número, por ejemplo 35g.
A su vez, cada grado centesimal se subdivide en unidades más pequeñas dividiéndolo en cien partes iguales, y dando lugar al minuto. Así, el minuto (m) en este sistema es la centésima parte del grado (1g = 100m) y el segundo (s) la centésima parte del minuto (1m = 100s).
De la misma manera, el segundo se divide en décimas, centésimas, milésimas,... Un ejemplo de un ángulo expresado según el sistema centesimal sería: 40g 30m 10s.
Por otro lado, el método para expresar en forma decimal un grado expresado en minutos y segundos centesimales es muy sencillo, ya que basta con colocar una coma después de los grados, así 40g 30m 10s = 40,3010g.
Y la conversión inversa, es decir, para pasar de grados centesimales en forma decimal a minutos y segundos centesimales se realiza como se indica en el siguiente ejemplo:
- Pasar 26,2547g a grados minutos y segundos centesimales
26,2547g = 26g + 0,25 · 100 + 0,0047 · 10000 = 26g + 25m + 47s
Aunque este sistema trató de ser el sustituto del sistema sexagesimal, por su facilidad de uso y mayor exactitud, al final el sistema centesimal no lo ha logrado, reservándose su uso sólo en algunas aplicaciones concretas como la topografía, construcción de carreteras o el uso artillero.
1.4- Milésima artillera
La milésima artillera o MIL ANGULAR es una unidad de medida de ángulos utilizada en el ámbito militar, principalmente en instrumentos de orientación y señalización.
La milésima artillera surge de la necesidad de aumentar la precisión en el uso de armamento cada vez más avanzado, y donde el uso de medidas angulares, como los grados sexagesimales o centesimales, no podían responder a esta necesidad debido a que son unidades de medidas demasiado grandes para las cada vez más modernas y potentes piezas de artillería. Por tanto, era necesaria una nueva y más precisa unidad de medida para los aparatos que proporcionaban los ángulos de alcance y deriva de los modernos cañones y demás armas. Nacía así la milésima artillera.
La nueva medida angular resultaba de dividir en 6400 partes iguales una circunferencia, en comparación de las sólo 360 divisiones de los grados sexagesimales o las 400 de los centesimales, y a cada una de estas partes se la denomina milésima artillera.
Por tanto, haciendo uso de la milésima artillera, un ángulo recto de 90º podía dividirse en 1600 partes iguales, por lo que se podía determinar más exactamente la posición de cualquier objetivo.
La milésima artillera, al igual que los grados sexagesimales o centesimales, es una medida angular que se puede definir también como el ángulo con el que vemos una varilla de un metro de alta a 1 Km. de distancia.
Gráficamente suele representarse con un triangulo rectángulo cuya base representa el Km de distancia y su otro cateto representa la medida de un metro. Finalmente el ángulo opuesto a dicho cateto es el que representa a la Milésima Artillera.
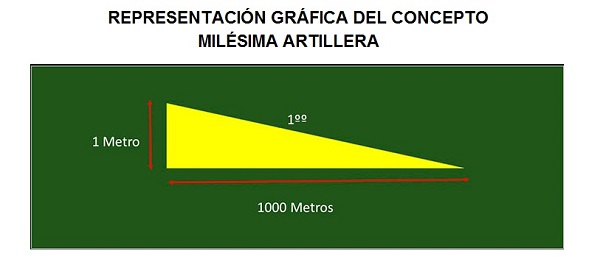
Como se ve en la figura anterior, una MIL es el ángulo con el que vemos los extremos de una varilla de 1 metro de longitud a 1 Km. de distancia.
Como conclusión a este apartado, se indica la relación entre el sistema sexagesimal, el sistema centesimal y la milésima artillera:
360º = 400g = 6400ºº
90º = 100g = 1600ºº
2- Métodos de conversión entre los sistemas de medida de ángulo
2.1- Pasar de radianes a grados sexagesimales
Para pasar de radianes a grados sexagesimales hay que recordar la relación para un ángulo que describe una circunferencia completa expresado en grados y radianes, como:
360º = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresadas en grados y radianes es la siguiente:
| G | = | R |
| 360º | 2 · π |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se desea es calcular los grados sexagesimales a partir de radianes, se despeja G de la expresión anterior, quedando:
|
R |
|
G = |
· 360º |
|
|
2·π |
|
- EJEMPLO 1: Pasar 1 radián a grados sexagesimales
Sustituyendo el valor de 1 radián en la expresión anterior resulta:
|
1 |
|
G = |
· 360º = 57,29578º |
|
|
2·π |
|
Por tanto, 1 rad = 57,29578º
También se puede expresar la medida de ángulo obtenida en forma compleja (grados minutos y segundos) de la siguiente forma:
Grados: 57,29578º = 57º + 0,29578º
Minutos: 0,29578º → 0,29578 · 60 = 17,7468´ → 17,7468´ = 17´+ 0,7468´
Segundos: 0,7468´ · 60 = 44,81´´
Por tanto, 1 rad = 57,29578º = 57º 17´ 44,81´´ (57 grados 17 minutos 44,81 segundos)
- EJEMPLO 2: Pasar π/4 radianes a grados sexagesimales
Sustituyendo π/4 en la expresión anterior se obtiene:
|
π/4 |
|
G = |
· 360º = 45º |
|
|
2·π |
|
Por tanto, π/4 rad = 45º. O también:
π/4 rad = 45º = 45º 0´ 0´´ (45 grados 0 minutos 0 segundos)
2.2- Pasar de radianes a grados centesimales
Para pasar de radianes a grados centesimales se parte de la relación que hay para un ángulo que describe una circunferencia completa expresado en grados centesimales y radianes:
400 g = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresadas en grados centesimales y radianes es la siguiente:
| C | = | R |
| 400g | 2 · π |
donde,
C es la medida del ángulo expresada en grados centesimales (g)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se pide es calcular los grados centesimales a partir de radianes, se despeja C de la expresión anterior, quedando:
|
R |
|
C = |
· 400 g |
|
|
2·π |
|
- EJEMPLO: Pasar 2 radianes a grados centesimales
Sustituyendo el valor de 2 radianes en la expresión anterior resulta:
|
2 |
|
C = |
· 400 g = 127,3240 g |
|
|
2·π |
|
Por tanto, 2 rad = 127,3240 g
El resultado anterior del ángulo se puede expresar también en forma compleja (grados minutos y segundos) de la siguiente forma:
Grados Centesimales: 127,3240g = 127g + 0,3240g
Minutos: 0,3240g → 0,3240 · 100 = 34,40m → 32,40m = 32m + 0,40m
Segundos: 0,40 · 100 = 40s
Por tanto, 2 rad = 127,3240 g = 127g 32m 40s (127 grados centesimales 32 minutos 40 segundos)
2.3- Pasar de grados sexagesimales a radianes
Para pasar de grados sexagesimales a radianes se parte de nuevo de la relación de un ángulo completo expresado en grados sexagesimales y radianes:
360º = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en grados sexagesimales y radianes es la ya conocida:
| G | = | R |
| 360º | 2 · π |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se desea es calcular el valor en radianes de un ángulo expresado en grados sexagesimales, se despeja R de la expresión anterior, quedando:
|
G |
|
R = |
· 2 · π |
|
|
360º |
|
- EJEMPLO 1: Pasar un ángulo de 45º a radianes
Sustituyendo el valor de 45º en la expresión anterior resulta:
|
45º |
|
R = |
· 2 · π = π/4 |
|
|
360º |
|
Por tanto, 45º = π/4 radianes.
- EJEMPLO 2: Pasar un ángulo de 60º 18´ 50´´ a radianes
En este caso se parte de un ángulo expresado en grados minutos y segundos y se quiere pasar a radianes.
En primer lugar, habrá que pasar el ángulo expresado en grados minutos y segundos (forma compleja) a simple (sólo en grados). Para pasar 60º 18´ 50´´ a forma simple (º) se opera de la siguiente forma:
1º) Los grados se dejan en grados: 60º → 60º
2º) Los minutos se pasan a grados: 18´ → 18´/60 = 0,3º
3º) Los segundos se pasan a minutos, y éstos a grados: 50´´ → 50´´/60 = 0,8333´ → 0,8333´/60 = 0,0139º
4º) Se suman todos los grados obtenidos: 60º + 0,3º + 0,0139º = 60,3139º
Por tanto, 60º 18´ 50´´ = 60,3139º
Ahora se opera como en el ejemplo anterior, para pasar de grados sexagesimales a radianes:
Sustituyendo el valor de 60,3139º en la expresión anterior resulta:
|
60,3139º |
|
R = |
· 2 · π = 1,0527 radianes |
|
|
360º |
|
Por tanto, 60º 18´ 50´´ = 1,0527 radianes.
2.4- Pasar de grados sexagesimales a grados centesimales
Para pasar de grados sexagesimales a centesimales se parte de la relación del ángulo que describe una circunferencia completa expresado en grados sexagesimales y centesimales:
1 vuelta completa = 360º = 400 g
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en grados sexagesimales y centesimales sería:
| G | = | C |
| 360º | 400 g |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
C es la medida del ángulo expresada en grados centesimales (g)
Si lo que se pide es calcular los grados centesimales a partir de grados sexagesimales, se despeja C de la expresión anterior, quedando:
|
G |
|
C = |
· 400 g |
|
|
360º |
|
- EJEMPLO 1: Pasar 90º sexagesimales a centesimales
Sustituyendo el valor de 90º en la expresión anterior resulta:
|
90º |
|
C = |
· 400 g = 100 g |
|
|
360º |
|
Por tanto, 90º = 100 g
- EJEMPLO 2: : Pasar un ángulo expresado en el sistema sexagesimal de 23º 37´ 45´´ a grados centesimales
En primer lugar, habrá que pasar el ángulo expresado en grados minutos y segundos (forma compleja) a simple (sólo en grados). Para pasar 23º 37´ 45´´ a forma simple (º) se opera de la siguiente forma:
1º) Los grados se dejan en grados: 23º → 23º
2º) Los minutos se pasan a grados: 37´ → 37´/60 = 0,6167º
3º) Los segundos se pasan a minutos, y éstos a grados: 45´´ → 45´´/60 = 0,75´ → 0,75´/60 = 0,0125º
4º) Se suman todos los grados obtenidos: 23º + 0,6167º + 0,0125º = 23,6292º
Por tanto, 23º 37´ 45´´ = 23,6292º
Ahora se aplica la expresión anterior para pasar de grados sexagesimales a centesimales:
|
23,6292º |
|
C = |
· 400 g = 26,2547 g |
|
|
360º |
|
Por tanto, 23,6292º = 26,2547 g
Por último, sólo faltará expresar los grados centesimales obtenidos en forma simple a forma compleja (grados, minutos y segundos centesimales):
Grados Centesimales: 26,2547g = 26g + 0,2547g
Minutos: 0,2547g → 0,2547·100 = 25,47m → 25,47m = 25m+ 0,47m
Segundos: 0,47m·100 = 47s
Por tanto, finalmente se tiene que: 23,6292º = 26,2547g = 26g 25m 47s
2.5- Pasar de grados centesimales a grados sexagesimales
Para pasar de grados centesimales a sexagesimales se parte, como en el apartado anterior, de la relación del ángulo que describe una circunferencia completa expresado en grados centesimales y sexagesimales:
1 vuelta completa = 400 g = 360º
Por tanto, de nuevo la expresión general que permite relacionar las medidas de un ángulo expresado en grados centesimales y sexagesimales sería:
| C | = | G |
| 400 g | 360º |
donde,
C es la medida del ángulo expresada en grados centesimales (g)
G es la medida del ángulo expresada en grados sexagesimales (º)
Si lo que se pide es calcular los grados sexagesimales a partir del ángulo expresado en grados centesimales, se despeja G de la expresión anterior, quedando:
|
C |
|
G = |
· 360º |
|
|
400 g |
|
- EJEMPLO 1: Pasar 90 g centesimales a grados sexagesimales
Sustituyendo el valor de 90 g en la expresión anterior resulta:
|
90 g |
|
G = |
· 360º = 81º |
|
|
400 g |
|
Por tanto, 90 g = 81º
- EJEMPLO 2: : Pasar un ángulo expresado en el sistema centesimal 43g 21m 58s a grados sexagesimales (expresando también el resultado en grados minutos segundos sexagesimales)
En primer lugar, habrá que pasar el ángulo expresado en grados minutos y segundos centesimales (forma compleja) a la forma simple (sólo grados). Para pasar 43g 21m 58s a forma simple (sólo grados) se opera de la siguiente forma:
1º) Los grados centesimales se dejan en grados centesimales: 43g → 43g
2º) Los minutos centesimales se pasan a grados centesimales: 21´ → 21´/100 = 0,21g
3º) Los segundos centesimales se pasan a minutos centesimales, y éstos a grados centesimales: 58´´ → 58´´/100 = 0,58´ → 0,58´/100 = 0,0058g
4º) Se suman todos los grados centesimales obtenidos: 43g + 0,21g + 0,0058g = 43,2158 g
Por tanto, 43g 21m 58s = 43,2158 g
Ahora se aplica la expresión anterior para pasar de grados centesimales a grados sexagesimales:
|
43,2158 g |
|
G = |
· 360º = 38,8942º |
|
|
400 g |
|
Por último, sólo faltará expresar los grados sexagesimales obtenidos a la forma compleja (grados, minutos y segundos), de la siguiente forma:
Grados: 38,8942º = 38º + 0,8942º
Para obtener los minutos: 0,8942º → 0,8942 · 60 = 53,6520´ → 53,6520´ = 53´+ 0,6520´
Para obtener los segundos: 0,6520´ · 60 = 39,12´´
Por tanto, 43 g 21 m 58 s = 38,8942º = 38º 53´ 39,12´´ (38 grados 53 minutos 39,12 segundos sexagesimales)
2.6- Pasar milésimas artilleras a grados sexagesimales
La milésima artillera o mil angular es un sistema de medida de ángulos que resultaba de dividir en 6400 partes iguales una circunferencia completa. Por tanto, la relación entre milésimas artilleras y grados sexagesimales es la siguiente:
1 vuelta completa = 6400ºº = 360º
La relación anterior también se puede expresar en función del ángulo recto. En este caso, la milésima artillera es la que resulta de dividir un ángulo recto (90º en el sistema sexagesimal) en 1600 partes iguales, es decir, que:
¼ de vuelta = 1600ºº = 90º
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en milésimas artilleras y grados sexagesimales es la siguiente:
| MIL | = | G |
| 1600ºº | 90º |
donde,
MIL es la medida del ángulo expresada en milésimas artilleras (ºº)
G es la medida del ángulo expresada en grados sexagesimales (º)
Si lo que se pide es calcular los grados sexagesimales a partir del ángulo expresado en milésimas artilleras, se despeja G de la expresión anterior, quedando:
|
MIL |
|
G = |
· 90º |
|
|
1600ºº |
|
- EJEMPLO: Pasar 32ºº a grados sexagesimales
Sustituyendo el valor de 32ºº en la expresión anterior resulta:
|
32ºº |
|
G = |
· 90º = 1,8º |
|
|
1600ºº |
|
Por tanto, 32ºº = 1,8º
2.7- Pasar milésimas artilleras a grados centesimales
Como se ha dicho en el apartado anterior, la milésima artillera es la medida angular que resultaba de dividir en 6400 partes iguales una circunferencia completa, mientras que en grados centesimales una circunferencia completa son 400g, por tanto:
1 vuelta completa = 6400ºº = 400 g
Si se prefiere, la relación anterior también se puede expresar en función del ángulo recto. En este caso, la milésima artillera es la que resulta de dividir un ángulo recto (100g en el sistema centesimal) en 1600 partes iguales, es decir, que:
¼ de vuelta = 1600ºº = 100 g
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en milésimas artilleras y grados centesimales es la siguiente:
| MIL | = | C |
| 1600ºº | 100g |
donde,
MIL es la medida del ángulo expresada en milésimas artilleras (ºº)
C es la medida del ángulo expresada en grados centesimales (g)
Si lo que se pide es calcular los grados centesimales a partir del ángulo expresado en milésimas artilleras, se despeja C de la expresión anterior, quedando:
|
MIL |
|
C = |
· 100g |
|
|
1600ºº |
|
- EJEMPLO: Pasar de milésimas artilleras un ángulo de 20ºº a grados centesimales
Sustituyendo el valor de 20ºº en la expresión anterior resulta:
|
20ºº |
|
C = |
· 100g = 1,25g |
|
|
1600ºº |
|
Por tanto, 20ºº = 1,25g
También se puede expresar las 20 milésimas artilleras en grados, minutos y segundos centesimales. Para ello, habrá que pasar a forma compleja el anterior resultado:
Grados centesimales: 1,25g = 1g + 0,25g
Minutos centesimales: 0,25g → 0,25·100 = 25m
Por tanto, finalmente se tiene que: 20ºº = 1,25g = 1g 25m
2.8- Pasar de porcentaje en tanto por ciento a ángulo sexagesimal
La pendiente de una recta se suele dar como un porcentaje en tanto por ciento como una medida de su inclinación, por ejemplo, 7% que significa que por cada cien unidades de medida horizontal se varía en 7 unidades la cota vertical.
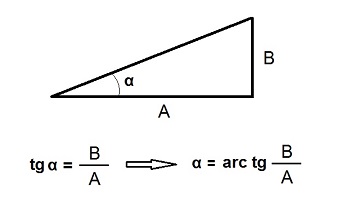
Aplicando la definición de la tangente trigonométrica de un ángulo, como se muestra en la figura adjunta, se puede obtener directamente el valor de ese ángulo mediante la función inversa de la tangente, es decir, la arcotangente.
- EJEMPLO: Pasar una pendiente del 15% a grados sexagesimales.
Siguiendo la nomenclatura utilizada en la figura adjunta para los parámetros, se tiene que para una pendiente del 15%
A = 100
B = 15
Por tanto, el ángulo de inclinación α = arc tg (15/100) = 8,53º
Ir a
Tutoriales
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055
