— Tutorial nº 129 —
Cálculo de Muelles Helicoidales
Índice de contenidos:
1- Introducción
1.1- Generalidades
1.2- Material de los muelles
2- Muelles helicoidales a compresión
2.1- Constante elástica del muelle
2.2- Análisis de esfuerzos
2.3- Cálculo estático y a fatiga
2.4- Deformación del muelle
3- Muelles helicoidales a torsión
3.1- Generalidades
3.2- Análisis de esfuerzos
3.3- Deformación angular del muelle
3.4- Constante elástica del muelle a torsión
4- Frecuencia crítica de los muelles helicoidales
4.1- Generalidades
4.2- Cálculo de la frecuencia crítica
5- Capacidad de los muelles para el almacenamiento de energía
DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Generalidades
Los muelles, también llamados resortes, son elementos mecánicos que tienen la capacidad de deformarse ante la actuación de un esfuerzo, y que pueden recuperar su estado inicial una vez haya cesado el esfuerzo actuante sobre el muelle.

Como consecuencia de la deformación, los muelles acumulan una energía que, una vez haya cesado el esfuerzo que actúa sobre el muelle, es liberada mediante una fuerza o momento de recuperación que consigue volver al muelle a su estado inicial, y que se puede considerar, en la mayoría de los casos, de una magnitud proporcional al valor de la deformación lineal o angular sufrida por el muelle.
Los muelles o resortes tienen múltiples aplicaciones, entre los que destaca su empleo como elementos en la suspensión de vehículos debido a la flexibilidad que proporcionan, también como sistema para ejercer esfuerzos, o como elementos para almacenar o absorber energía.
En otras ocasiones, los muelles se pueden utilizar en aquellos mecanismos diseñados para asegurar el contacto permanente entre dos piezas, para acelerar movimientos que necesitan de una gran rapidez, o para limitar los efectos de choques y vibraciones, etc.
En este tutorial se van a estudiar los muelles de tipo helicoidales, que están fabricados de un alambre enrollado formando una espira y que sirven para resistir principalmente esfuerzos actuantes de tracción, compresión o de torsión sobre el muelle.
1.2- Material de los muelles
Debido a la gran capacidad de deformación que deben soportar los muelles, es necesario que para su fabricación se empleen aquellos tipos de aceros que puedan ofrecer una gran elasticidad, como son los aceros al carbono, aceros al silicio, aceros al cromo-vanadio, aceros al cromo-silicio, etc.
En algunas otras aplicaciones especiales es posible utilizar otros materiales para la fabricación de muelles, además del acero, como son el cobre endurecido y el latón.
No obstante, como el acero es de los materiales más empleados, en la siguiente tabla se muestran las propiedades y designación de los tipos aceros más usados para la fabricación de muelles:
Tabla 1. Tipos de Aceros para Muelles |
|||||||||||
Designación |
Norma Vigente |
Normas Nacionales |
Campo de Aplicación |
Propiedades Mecánicas |
|||||||
Simbólica |
Numérica |
UNE |
AFNOR |
DIN |
AISI/SAE |
Dureza |
Re (N/mm2) |
Rm (N/mm2) |
Tenacidad (J) |
||
38Si7 |
1.5023 |
EN 10089 |
F 1451 |
41 S 7 |
38Si7 |
- |
Arandela de muelles, tensores para el sector de la cosntrucción |
máx. 217 HB |
≥ 1030 |
1180 - 1370 |
- |
61SiCr7 |
1.7108 |
EN 10089 |
F 1442 |
61 SC 7 |
60SiCr7 |
9262 |
Muelles para el sector marítimo, la construcción y la maquinaria |
máx. 248 HB |
≥ 1150 |
1350 - 1600 |
≥ 5 |
55Cr3 |
1.7176 |
EN 10089 |
F 1431 |
55 C 3 |
55Cr3 |
5155 / 5160 |
Muelles aptos para piezas de mayores dimensiones |
máx. 248 HB |
≥ 1200 |
1400 - 1650 |
≥ 9 |
51CrV4 |
1.8159 |
EN 10089 |
F 1430 / F 143 |
51 CV 4 |
50CrV4 |
6145 / 6150 |
Acero estándar de muelles, para cargas elevadas (1370 - 1720 N/mm2) |
máx. 248 HB |
≥ 1200 |
1400 - 1700 |
≥ 9 |
52CrMoV4 |
1.7701 |
EN 10089 |
- |
51 CDV 4 |
51CrMoV4 |
- |
Acero para muelles para cargas elevadas y de mayores secciones |
máx. 248 HB |
≥ 1200 |
1400 - 1700 |
≥ 6 |
(*) Para más información, consultar el Tutorial nº 101 "Estudio y Clasificación de los Aceros"
En general, los muelles suelen dividirse en dos grandes grupos, que son los muelles de alambre y los muelles de lámina.
Los muelles de alambre, que son fabricados por alambres enrollados que pueden ser de sección redonda o cuadrada, comprenden a los muelles helicoidales, que son el objeto de estudio de este tutorial, y sirven para resistir esfuerzos de tracción, compresión o torsión. Por su parte, los muelles de láminas pueden dividirse a su vez en muelles de tipo elíptico o de voladizo.
2- Muelles helicoidales a compresión
2.1- Constante elástica del muelle
Este tutorial se va a centrar en el estudio de los muelles o resortes de tipo helicoidales, fabricados de alambre con sección redonda, y enrollado formando espiras.
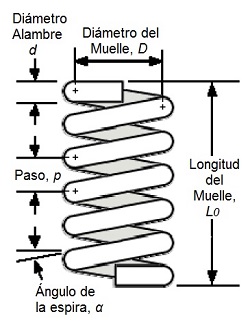
En la figura esquemática adjunta se puede consultar los distintos parámetros geométricos que definen a un muelle helicoidal tipo:
D diámetro del muelle
d diámetro del alambre
p paso de la espira del muelle
α ángulo de la espira del muelle
Na número de espiras activas del muelle
Aunque en apartados posteriores se volverá a tratar con más profundidad, se define la constante elástica (K) del muelle como la relación entre la fuerza actuante sobre el muelle y la deformación que origina, es decir:
K = F / y
donde,
y es el valor de la deformación en dirección axial producida en el resorte
F es el valor de la fuerza axial ejercida sobre el extremo del resorte.
(*) Si la fuerza aplicada (F) se mide en newton (N) y la deformación del muelle en metros (m), las unidades de medida para la constante del muelle (K) será de newton/metro (N/m).
La expresión anterior será válida siempre y cuando la tensión del muelle no exceda el límite elástico del material del alambre.
Para el caso concreto de muelles helicoidales sometidos a un esfuerzo de compresión o extensión, conocido el módulo de cizalladura (G) del material del que está fabricado las espiras del muelle, la expresión que permite calcular de manera directa la constante elástica del muelle es la siguiente:
|
G · d4 |
|
K = |
|
|
|
8 · D3 · Na |
|
donde,
G es el módulo de cizalladura del alambre del muelle
D es el diámetro de la espira del muelle
d es el diámetro del alambre
Na es el número de espiras activas del muelle.
2.2- Análisis de esfuerzos
Supongamos a continuación un muelle helicoidal sometido a una carga (F) de compresión, como la que se muestra en la figura siguiente que se acompaña.
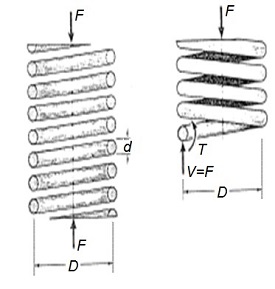
La carga (F) axial aplicada en el extremo del resorte originará un esfuerzo de cortadura (V) y una torsión (T) en el alambre de la espira, de valores:
V = F
T = F · D/2
Estos esfuerzos darán lugar en la sección del alambre de tensiones tangenciales, tanto debido al momento torsor (T) como al esfuerzo de cortadura (V), de valores:
• Tensiones tangenciales debidas al momento torsor (T):
τT = T / (π·d3/16) = 8·F·D / π·d3
• Tensiones tangenciales debidas al esfuerzo cortante (V):
τV = 1,23·F / (π·d2/4) = (0,615/c)·(8·F·D / π·d3)
donde c = D/d es el llamado índice del resorte.
La tensión tangencial resultante será la suma de ambas tensiones:
τ = τT + τV = (1+0,615/c) · (8·F·D / π·d3) = Ks · (8·F·D / π·d3)
donde Ks es el llamado coeficiente de multiplicación de la tensión de valor:
|
0,615 |
|
Ks = 1 + |
|
|
|
c |
|
No obstante, este factor sólo tiene en cuenta los efectos debidos al cizallamiento puro, pero no los incrementos de tensión producidos por la curvatura del alambre.
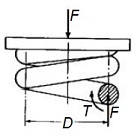
En efecto, la forma curva de la espira del muelle genera una concentración de tensiones en las fibras más interiores de la sección del alambre, que origina una distribución de tensiones en la sección diferente a la del caso de una barra recta tensionada.
Por tanto se tiene que, por un lado, debido a la curvatura se produce una concentración de tensiones porque la longitud de las fibras interiores del alambre son más cortas que las exteriores, y por otro lado además, en las fibras interiores del alambre también se va a originar una mayor concentración de tensión debido a que a la tensión tangencial (τV) pura debida al esfuerzo cortante (F) se le suma la tensión tangencial de torsión (τT), mientras que en la fibra más externa de la sección se resta.
Con la siguiente figura que se adjunta, se pretende ilustrar cómo es la superposición de tensiones que se produce en la sección del alambre de un muelle helicoidal.
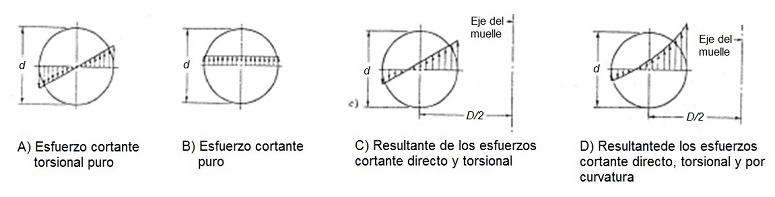
Así pues, debido a ambos factores, curvatura del alambre y superposición de esfuerzos cortante y de torsión, resulta que el nivel de tensiones que se alcanza en las fibras interiores de las espiras del resorte va a ser mayor (Figuras C y D).
Para solventar analíticamente esta situación, Wahl ofrece una corrección que permite obtener una fórmula fundamental de torsión empleando un coeficiente de concentración de tensiones (Kw) que va a tener en cuenta ambos factores: una concentración de tensiones en las fibras más interiores debido a la curvatura, y en segundo lugar, el incremento de la tensión tangencial pura debido a que el efecto de la carga axial (F) se suma al del momento torsor (T).
En este caso, la expresión que propone Wahl para calcular la tensión tangencial en el alambre del muelle será la siguiente:
τ = [(4c-1)/(4c-4)+0,615/c] · (8·F·D / π·d3) = Kw · (8·F·D / π·d3)
donde Kw es el factor de corrección de Wahl.
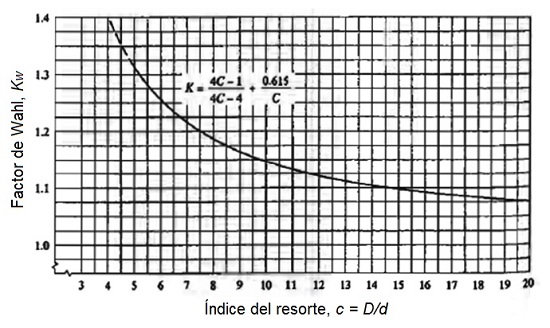
Por tanto, el factor de corrección de Wahl o coeficiente de concentración de tensiones se puede obtener por la siguiente expresión:
| Kw = | 4·c - 1 | + | 0,615 |
| 4·c - 4 | c |
donde c = D/d es el índice del resorte.
No obstante, el factor de corrección de Wahl (Kw) también puede ser obtenido, además de por la fórmula anterior, a partir de la siguiente gráfica que resulta válida para muelles helicoidales de alambre redondo.
2.3- Cálculo estático y a fatiga
A continuación se proponen las ecuaciones que se deben emplear para el cálculo de las tensiones que se originan en resortes, tanto cuando se encuentren sometidos a cargas estáticas como a fatiga (bajo cargas alternadas).
• Cálculo estático:
Cuando el resorte se encuentra sometido a cargas estáticas puede despreciarse el efecto de curvatura del muelle. En este caso, para el cálculo de la tensión que alcanza el muelle se recomienda emplear la expresión ya vista en el apartado anterior:
τ = Ks · (8·F·D / π·d3)
siendo
F el valor de la carga que actúa sobre el muelle
D es el diámetro de la espira del muelle
d es el diámetro del alambre
y donde Ks es el coeficiente de multiplicación de la tensión de valor:
|
0,615 |
|
Ks = 1 + |
|
|
|
c |
|
donde c = D/d es el índice del resorte.
Una vez calculado el valor de la tensión tangencial (τ) alcanzada en el resorte, para que éste no llegue a su agotamiento deberá cumplirse que:
τ ≤ τadm
donde τadm es la tensión de cortadura admisible del acero del alambre.
• Cálculo a fatiga:
Cuando el resorte se encuentra sometido a una carga alternada de amplitud F, para el cálculo de la tensión máxima se recomienda emplear la expresión que utiliza el factor de Wahl, ya vista en el apartado anterior:
τ = [(4c-1)/(4c-4)+0,615/c] · (8·F·D / π·d3) = Kw · (8·F·D / π·d3)
siendo
F el valor de la amplitud de la carga variable
D es el diámetro de la espira del muelle
d es el diámetro del alambre
y donde Kw es el factor de corrección de Wahl que se calcularía siguiendo también lo indicado en el apartado anterior.
Una vez calculado el valor de la tensión tangencial (τ) alcanzada en el resorte aplicando la expresión anterior, para que éste no llegue a su agotamiento deberá cumplirse que:
τ ≤ τadm = α·σu
siendo σu la carga de rotura a tracción del material del resorte, y α es un coeficiente de seguridad que dependerá del tipo de servicio, tomando los siguientes valores:
α=0,405 → para servicio ligero, N < 104 ciclos
α=0,324 → para servicio medio, 104 < N < 105 ciclos
α=0,263 → para servicio intenso, N > 106 ciclos.
2.4- Deformación del muelle
En este apartado se va a tratar de obtener una formulación de la ley de deformación, mediante la cual, se podrá calcular la deformación (y) que experimenta un muelle helicoidal en función de la carga axial (F) aplicada en sus extremos.
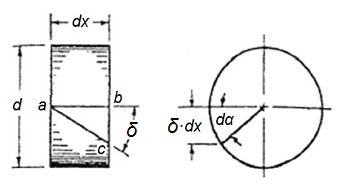
Para estudiar cómo se deforma el alambre que forma la espira del resorte, se considerará una rebanada o porción de alambre entre dos secciones rectas muy próximas separadas un diferencial de longitud dx.
En la figura adjunta se puede ver el trozo de diferencial de longitud (dx) de alambre de diámetro (d) que forma parte de la espira del muelle.
En la rebanada de alambre (dx) se indica también la línea recta ab, que es paralela al eje del muelle cuando el muelle no está deformado.
Así, cuando sobre el resorte actúa una carga axial (F), éste se deforma, haciendo girar el trozo de alambre un ángulo (δ). De esta manera, la línea ab pasará a ocupar una nueva posición indicada por ac.
Aplicando la ley de Hooke para tensiones tangenciales originadas por los esfuerzos de torsión del muelle, se tiene la siguiente relación entre la tensión (τ) aplicada y la deformación (δ) originada:
|
τ |
|
δ = |
|
|
|
G |
|
donde G es el módulo de cizalladura del alambre del muelle.
Del apartado 2.2, se veía que el valor de la tensión (τ) de la sección del alambre del muelle, cuando sobre éste actúa una carga (F), se podía expresar en función del factor de corrección de Wahl, como:
τ = Kw · (8·F·D / π·d3)
siendo
F el valor de la carga aplicada
D es el diámetro de la espira del muelle
d es el diámetro del alambre
y donde Kw es el factor de corrección de Wahl.
Al considerarse un diferencial de longitud (dx) de trozo de alambre, el efecto de la curvatura en esa porción es prácticamente nulo. Por ello, el factor de corrección de Wahl, en este caso, se puede considerar igual a la unidad (Kw = 1).
De esta manera, si se sustituye el valor de la tensión (τ) considerando el factor de Wahl igual a uno (Kw = 1), la expresión anterior de la ley de Hooke quedaría expresada de la siguiente forma:
|
8 · F · D |
|
δ = |
|
|
|
G · π · d3 |
|
Por otro lado, según la figura indicada anteriormente de la rebanada de alambre (dx), la longitud de la línea indicada en el dibujo por bc se puede expresar también como:
bc = δ · dx
Pero el ángulo que gira una sección del alambre respecto a la otra separada un diferencial de longitud (dx) vale:
|
δ · dx |
|
dα = |
|
|
|
d/2 |
|
es decir,
|
2 · δ · dx |
|
dα = |
|
|
|
d |
|
Sustituyendo el valor de (δ) por la obtenida anteriormente de la ley de Hooke se tendrá que:
|
2 · 8 · F · D · dx |
|
dα = |
|
|
|
d · G · π · d3 |
|
es decir,
|
16 · F · D · dx |
|
dα = |
|
|
|
G · π · d4 |
|
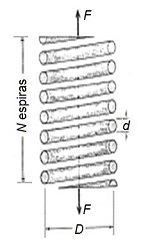
Por otro lado, si se considera que el muelle helicoidal objeto de estudio está formado por N espiras activas, el desarrollo o longitud total del alambre se calcula como:
L = π · D · N
donde,
L es el desarrollo o longitud total del alambre que forma la espira del muelle
D es el diámetro de la espira del muelle
N es el numero de espiras activas que forman el muelle.
Pues bien, la deformación angular que se produce en uno de los extremos del muelle respecto al otro, cuando actúa una carga axial (F), se obtiene integrando entre el valor de cero y la longitud total del alambre (L = π·D·N), del diferencial de ángulo (dα) que gira una sección del alambre respecto a la otra que está separada un diferencial de longitud (dx):
|
2 · δ · dx |
|
α = ∫0π·D·N dα = ∫0π·D·N |
|
|
|
d |
|
Resolviendo la integración anterior entre los límites x=0 y por otro lado, x=π·D·N, resulta finalmente un ángulo de giro de una sección respecto a otra de valor:
|
16 · F · D2 · N |
|
α = |
|
|
|
G · d4 |
|
Por otro lado, la carga (F) actuante tiene un brazo de momento igual a D/2, siendo D el diámetro de la espira, por lo que la deformación (y) originada en el muelle se obtiene como:
|
D |
|
y = α · |
|
|
|
2 |
|
Que sustituyendo el valor del ángulo de giro (α) por el valor obtenido anteriormente resulta finalmente la ley de deformación para un muelle helicoidal sometido a compresión/expansión:
|
8 · F · D3 · N |
|
y = |
|
|
|
G · d4 |
|
A partir de esta expresión se puede obtener también la constante elástica (K) de un muelle helicoidal, que ya fue vista en el apartado 2.1.
Efectivamente, según se indicaba en el apartado 2.1, la constante elástica (K) del muelle se define como la relación entre la fuerza (F) actuante y la deformación (y) que origina:
|
F |
|
K = |
|
|
|
y |
|
Sustituyendo la expresión anterior que proporciona la deformación (y) del muelle, se podrá obtener también la constante elástica (K) del muelle, como:
|
G · d4 |
|
K = |
|
|
|
8 · D3 · N |
|
Que es la misma expresión que la mostrada en el apartado 2.1.
3- Muelles helicoidales a torsión
3.1- Generalidades
Los muelles helicoidales a torsión son muy útiles para aquellas aplicaciones donde se necesite de la aplicación de un par torsor, como pueda ser en bisagras de puertas para mantenerlas cerradas, en los starters de vehículos, etc.
En los muelles que trabajan a torsión se genera una tensión de tipo normal en la sección del alambre del muelle, en contraste con la que se origina en los muelles helicoidales que trabajan a compresión o a extensión donde la tensión de la sección del alambre es de tipo tangencial.
Por tanto, en los muelles helicoidales a torsión ocurre que las tensiones residuales que surgen durante el arrollamiento del muelle están en la misma dirección que las tensiones de trabajo que se producen durante su utilización.
Estas tensiones residuales son de gran utilidad porque consiguen que el muelle sea más fuerte, oponiéndose a la tensión de trabajo, siempre y cuando la carga se aplique de modo que haga que el muelle se arrolle aún más.
Debido a que la tensión residual se opone a la de trabajo, los muelles a torsión pueden proyectarse para funcionar con unos límites de tensión que igualen o incluso excedan al límite de fluencia del alambre.
3.2- Análisis de esfuerzos
Un muelle a torsión está sometido a la acción de un esfuerzo de momento M=F·r, que genera una tensión normal en la sección del alambre que se puede expresar de la siguiente forma:
|
M |
|
σ = K · |
|
|
|
W |
|
donde K es un coeficiente de concentración de tensiones que va a tener en cuenta el fenómeno de concentración de tensiones debido a la curvatura del alambre del muelle.
Por otro lado, W es el módulo resistente a flexión de la sección del alambre, que se expresa a su vez como:
W = I/c = (π·d4/64)/(d/2) = π·d3/32
Por la tanto, la expresión que proporciona la tensión para el caso de muelles helicoidales de alambre redondo sometidos a esfuerzos de torsión, resultará ser:
|
32 · F · r |
|
σ = K · |
|
|
|
π · d3 |
|
El coeficiente de concentración de tensiones (K), que tendrá en cuenta los efectos de la curvatura del alambre, dependerá a su vez de la forma de éste, y de si se está considerando la tensión en la fibra interna o externa del arrollamiento del alambre.
Wahl determinó analíticamente cómo calcular el coeficiente K para muelles a torsión con alambres de sección cilíndrica, según se considere la fibra interna o externa del arrollamiento:
|
4·c2 - c - 1 |
|
Kinterna = |
|
|
|
4·c · (c - 1) |
|
|
4·c2 + c - 1 |
|
Kexterna = |
|
|
|
4·c · (c + 1) |
|
donde c = D/d es el índice del resorte.
3.3- Deformación angular del muelle
Para calcular la deformación angular (θ) se deberá partir de la expresión que proporciona la energía de deformación (U) del muelle sometido a un momento M = F·r, que viene calculado como:
|
M2 dx |
|
U = ∫ |
|
|
|
2 E I |
|
Integración que deberá extenderse a toda la longitud del alambre, es decir, entre los límites x=0 hasta x=π·D·N.
Por otro lado, el teorema de Castigliano establece que cuando actúan fuerzas sobre sistemas elásticos, el desplazamiento (Δ) correspondiente seguido por cualquier fuerza, puede obtenerse a partir de la derivada parcial de la energía de deformación respecto a esa fuerza, es decir:
|
dU |
|
Δ = |
|
|
|
dF |
|
En este caso, la fuerza F de deformación se desplazará a través de la distancia r·θ, donde θ es la deformación angular total del muelle. Por tanto, aplicando el teorema de Castigliano se tendrá que:
|
dU |
|
Δ = r·θ = |
|
|
|
dF |
|
Sustituyendo la expresión de la energía de deformación (U) en la expresión anterior resulta que:
| r·θ = ∫0π·D·N | d | F2 r2 dx | |
| dF | 2 E I |
que resulta,
|
F r2 dx |
|
r·θ = ∫0π·D·N |
|
|
|
E I |
|
donde para un alambre redondo se tiene que I=π·d4/64.
Por último, despejando la deformación angular (θ) y resolviendo la integración de la expresión anterior, resulta finalmente:
|
64 · F · r · D · N |
|
θ = |
|
|
|
E · d4 |
|
donde E es el módulo de elasticidad del material del que está hecho el alambre del muelle.
3.4- Constante elástica del muelle a torsión
La constante elástica (K) del muelle a torsión se define como la relación entre el par de torsión de la fuerza (F) actuante y la deformación angular (θ) que origina en el muelle:
|
F · r |
|
K = |
|
|
|
θ |
|
La constante (K) del muelle a torsión se suele expresar en unidades de kg·cm por radián, y se puede explicar también su significado como el par necesario para arrollar el muelle una vuelta.
Sustituyendo la expresión que proporciona la deformación angular (θ) del apartado anterior, entonces se podrá obtener también la constante elástica (K) del muelle a torsión, como:
|
E · d4 |
|
K = |
|
|
|
64 · D · N |
|
donde,
E es el módulo de elasticidad del alambre del muelle
d es el diámetro del alambre
D es el diámetro de la espira del muelle
N es el numero de espiras activas que forman el muelle.
4- Frecuencia crítica de los muelles helicoidales
4.1- Generalidades
En multitud de ocasiones, los muelles de espiras helicoidales se emplean en aplicaciones donde se les somete a trabajos que suponen movimientos alternativos muy rápidos, y donde los muelles se encuentran sometidos a cargas de tipo dinámicas, como por ejemplo, en el caso de los muelles empleados para el cierre y apertura de las válvulas de los motores de combustión.
Para estos casos, es muy importante que la frecuencia natural del muelle se encuentre lo suficientemente alejada del valor de la frecuencia de aplicación de la carga exterior que actúa sobre el resorte.
Si no se cumple la anterior condición y ambas frecuencias son similares, el muelle podría entrar en resonancia a la misma frecuencia que el movimiento aplicado. En esta situación, y puesto que los muelles helicoidales carecen prácticamente de capacidad de amortiguamiento, las tensiones internas en la resonancia serían elevadas y terminarían por agotar prematuramente la vida útil del resorte.
4.2- Cálculo de la frecuencia crítica
Por tanto, cuando un resorte esté sometido a cargas dinámicas es muy importante conocer su frecuencia natural, o frecuencia crítica, e imponer cierta condición en su diseño para que resulte una frecuencia natural del muelle que sea sensiblemente superior a las frecuencias de aplicación de las cargas dinámicas exteriores actuantes sobre el propio muelle.
En la práctica y como buen criterio en el diseño de muelles, se recomienda que la frecuencia natural de los resortes empleados en aplicaciones con cargas dinámicas sean del orden de 15 a 20 veces superior a la frecuencia de aplicación de la fuerza exterior, con objeto de evitar así fenómenos de resonancia.
Para el cálculo de la frecuencia natural (ω) de un muelle, que se suele expresar en ciclos por segundo, se pueden emplear las siguientes formulaciones, cuyo uso de cada una de ellas dependerá de las condiciones de apoyo de los extremos del resorte:
• Muelle con los extremos Libre-Libre:
| ω = | d | · √ | G |
| D2 · N | 2 · ρ |
• Muelle con los extremos Fijo-Libre:
| ω = | d | · √ | G |
| 2 · D2 · N | 2 · ρ |
• Muelle con los extremos Fijo-Fijo:
| ω = | d | · √ | G |
| D2 · N | 2 · ρ |
donde,
G es el módulo de cizalladura del alambre del muelle
d es el diámetro del alambre
D es el diámetro de la espira del muelle
N es el número de espiras activas del muelle
ρ es la densidad del material de fabricación del muelle (7,85 kg/dm3 para el acero).
5- Capacidad de los muelles para el almacenamiento de energía
La diversidad de aplicaciones mecánicas que tienen los muelles helicoidales los hace que sean elementos muy frecuentes en el diseño de máquinas y mecanismos de muy diversos tipos.
Unas veces interesa utilizar muelles para que absorban cargas de choque o de impacto, y en otras, como elementos que sean capaces de almacenar energía y que a la vez ocupen poco espacio. Si se utilizan los resortes para esta última aplicación, entonces tiene una vital importancia conocer la capacidad del muelle para almacenar energía.
Dependiendo si el muelle se somete a tensión de tipo axial, o bien si la tensión es de cizalladura, las ecuaciones que proporcionan la energía de deformación de un muelle son las siguientes:
• Para muelles sometidos a tensión axial, o muelles de clase E:
|
σ2 |
|
u = |
|
|
|
2 · E |
|
• Para muelles sometidos a tensión de cizalladura, o muelles de clase G:
|
τ2 |
|
u = |
|
|
|
2 · G |
|
donde u es la energía de deformación por unidad de volumen ocupado por el muelle.
No obstante, la tensión interna no se distribuye uniformemente a los largo de las espiras del muelle, por lo que a las anteriores expresiones se les afecta de un coeficiente de forma (CF), cuyo valor será menor de la unidad, y que tendrá en cuenta este hecho para el cálculo de la verdadera energía acumulada en el muelle.
De esta forma, y dependiendo del tipo de muelle, las ecuaciones de la energía de deformación de un muelle serán finalmente las siguientes:
• Para muelles sometidos a tensión axial, o muelles de clase E:
|
σ2 |
|
u = CF · |
|
|
|
2 · E |
|
• Para muelles sometidos a tensión de cizalladura, o muelles de clase G:
|
τ2 |
|
u = CF · |
|
|
|
2 · G |
|
Evidentemente, si CF = 1, que es el valor máximo que puede tomar el coeficiente de forma, significaría que la tensión se distribuye de manera uniforme a lo largo de todas las espiras activas del muelle, y el material del muelle se emplearía con la máxima eficacia. Pero generalmente esto no ocurre así, sino que la tensión no se distribuye uniformemente y por tanto el coeficiente CF será menor que la unidad (CF < 1).
Por tanto, el coeficiente de forma (CF) representa, o más bien, es una medida de la eficacia y capacidad del muelle para almacenar energía cuando éste se deforma.
En la siguiente tabla se incluyen algunos valores del coeficiente de forma (CF) calculados por Maier dependiendo del modelo de resorte, que resultan útiles conocer para la selección de muelles con fines de almacenamiento de energía:
Tabla 2. Valores del Coeficiente de Forma, CF |
||
Muelle |
Tipo |
CF |
Barra a tracción |
E |
1,0 |
Muelle de reloj |
E |
0,33 |
Muelle a torsión |
E |
0,25 |
Arandelas Belleville |
E |
0,05 - 0,20 |
Viga en voladizo |
E |
0,11 |
Tubo a torsión |
G |
0,90 aprox. |
Barra a torsión |
G |
0,50 |
Muelle a compresión |
G |
0,35 aprox. |
A continuación, se muestra varios ejemplos de cómo calcular el coeficiente de forma (CF) para distintos tipos de resortes.
• Muelle helicoidal trabajando a tracción o compresión
Se parte de las ecuaciones de la energía de deformación, que para un muelle helicoidal a tracción o compresión, se pueden escribir de la siguiente forma:
| u = | U | = | F · y |
| v | 2 · v |
donde,
F es la fuerza de tracción o compresión que actúa sobre el muelle
y es la deformación que origina en el muelle
v es el volumen que ocupa el alambre activo que forma las espiras del muelle.
Y por otro lado, como se cumple que:
y = 8·F·D3·N / (d4·G)
τ = 8·F·D·K / (π·d3)
v = (π·D·N)·(π·d2/4)
Por lo que la ecuación anterior que proporciona la energía de deformación del muelle también se puede expresar como:
| u = | 1 | · | τ2 |
| 2 · K2 | 2 · G |
Como al principio de este apartado se indicaba que la ecuación de la energía de deformación era de la forma:
|
τ2 |
|
u = CF · |
|
|
|
2 · G |
|
Comparando ambas expresiones se puede deducir que el coeficiente de forma CF = 1/(2K2).
Un valor habitual para la constante elástica de muelles helicoidales es K=1,20, por lo que de esta forma resultará un coeficiente CF = 0,35, valor que concuerda con lo indicado en la tabla anterior para muelle a compresión.
• Resorte constituido por una barra a torsión
De la misma manera, se puede calcular el coeficiente de forma (CF) para una barra a torsión, que trabajaría a modo de resorte.
Como en el caso anterior, se parte de las ecuaciones para la energía de deformación, que también se pueden escribir de la siguiente forma:
| u = | U | = | T · θ |
| v | 2 · v |
donde θ es el ángulo de giro con que se torsiona la barra.
En este caso, se tiene además que:
τ = 16T/πd3
θ = 32Tl/(πd2/4)
Y por lo tanto, la ecuación que proporciona la energía de deformación de la barra a torsión también se puede expresar como:
| u = | 1 | · | τ2 |
| 2 | 2 · G |
Y por consiguiente, resultaría que CF = 0,50, valor que también concuerda con lo indicado en la tabla anterior para el caso de barra a torsión.
>> FIN DEL TUTORIAL
Programa de Colaboración
Ahora puedes colaborar en el sostenimiento de esta web realizando un pequeño donativo
Gracias por tu colaboración
Hermenegildo Rodríguez Galbarro
Editor y Responsable de esta Web. [+info]
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055
