— Tutorial nº 206 —
Cálculo de Instalaciones de
Bombeo de Agua
Índice de contenidos:
1- Introducción
1.1- Fundamentos
1.2- Tipos de bombas de agua
2- Parámetros de funcionamiento
2.1- Potencia de la bomba
2.2- NPSH (ANPA)
2.3- Diseño de la aspiración
3- Procedimiento de cálculo
3.1- Diámetro de tubería
3.2- Altura manométrica
3.3- Elección del tipo de bomba
3.4- Comprobación de ausencia de cavitación
4- Ejemplo de cálculo
ANEXOS:
Anexo nº 1.- Catálogos de conductos y tuberías de agua
• Tuberías de Polietileno (PE)
• Tuberías de Polipropileno (PP-R)
• Tuberías y Accesorios de PVC
• Tuberías de Acero Negro Galvanizado
• Tuberías de Fundición Dúctil
Anexo nº 2.- Catálogos de fabricantes de bombas de agua
• Bombas SACI
• Bombas WILO
Anexo nº 3.- Empresas de Suministros y Servicio Técnico
• Productos Soplantes Rotativos para Presión y Vacío PEDRO GIL S.L.DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Fundamentos
Una bomba de agua es una máquina hidráulica cuyo funcionamiento se basa en el Principio de Bernoulli, según el cual, en un fluido ideal sin viscosidad, ni rozamiento, e incompresible que se encuentra en circulación por un conducto cerrado, su energía permanece constante en cada punto de su recorrido.
La energía que posee un fluido en movimiento se compone de tres componentes:
• cinética: es la energía que posee el fluido debido a su velocidad de movimiento;
• de flujo: relacionado con la presión que posee;
• gravitatoria: debido a la altitud del fluido.
Estas tres componentes de la energía se correlacionan con los mismos términos que definen el Principio de Bernoulli:
v2·ρ |
|
+ P + ρ·g·h = constante |
|
2 |
siendo,
v, la velocidad del fluido;
ρ, la densidad del fluido;
P, la presión del fluido a lo largo de la línea de corriente;
g, la aceleración de la gravedad (9,81 m/s2);
h, es la altura que alcanza el fluido en la dirección de la gravedad desde una cota de referencia.
Pues bien, una bomba de agua es una máquina hidráulica que es capaz de transmitir energía al fluido que pasa a su través, convirtiendo la energía mecánica que recibe a través de su eje en una energía "hidráulica" para el fluido, aumentando su velocidad, su presión o su altura, o todas las componentes a la vez, según el Principio de Bernoulli.
1.2- Tipos de bombas de agua
Según el principio de su funcionamiento, las bombas de agua se clasifican en dos grandes grupos:
• Bombas volumétricas o de desplazamiento positivo
• Bombas rotodinámicas
- Bombas volumétricas o de desplazamiento positivo:
Se denominan así porque basan su funcionamiento en un órgano propulsor que genera de manera positiva un volumen o cilindrada. Este tipo de bomba dispone de una cámara donde se aloja el fluido y cuyo volumen varía cuando la bomba entra en funcionamiento.
En efecto, cuando las paredes de la cámara empujan al fluido que contiene en su interior provoca un aumento de la presión de éste, aumentando la energía del fluido.
A su vez, este tipo de bombas se subdividen en:
Aternativas: pueden ser de émbolo o de membrana, y donde el volumen que confina el fluido varía por la acción de un émbolo o de una membrana, respectivamente. En este tipo de bombas el movimiento del fluido es discontinuo, en pulsaciones, donde la aspiración y descarga del agua se realiza por la acción coordinada de válvulas.
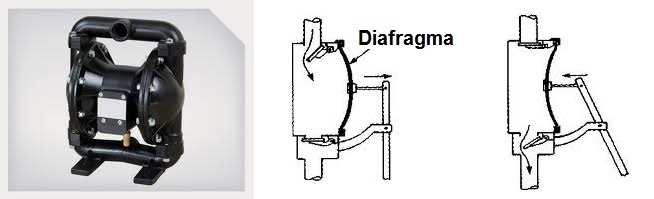
Figura 1. Bomba de membrana o diafragma. Esquema de funcionamiento
Rotativas: en este tipo de bombas el fluido se desplaza dentro de la cámara, desde una zona de baja presión hasta otra zona de alta presión donde está la salida. Según el órgano propulsor que mueve el fluido, pueden ser de paletas, de lóbulos, bombas de tornillo o de engranajes.
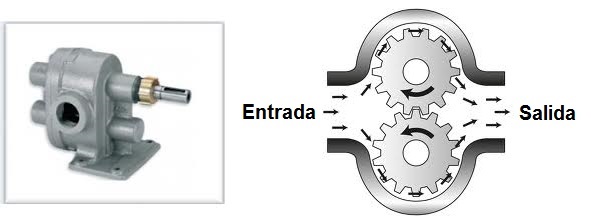
Figura 2. Bomba de engranajes. Esquema de funcionamiento
- Bombas rotodinámicas:
En este tipo de bombas existen uno o más rodetes girando a gran velocidad y que aspiran el fluido. El rodete le comunica la energía cinética de rotación al fluido que es lanzado a gran velocidad hacia las paredes de la voluta, que al chocar convierte parte de la energía cinemática que lleva el fluido en presión.
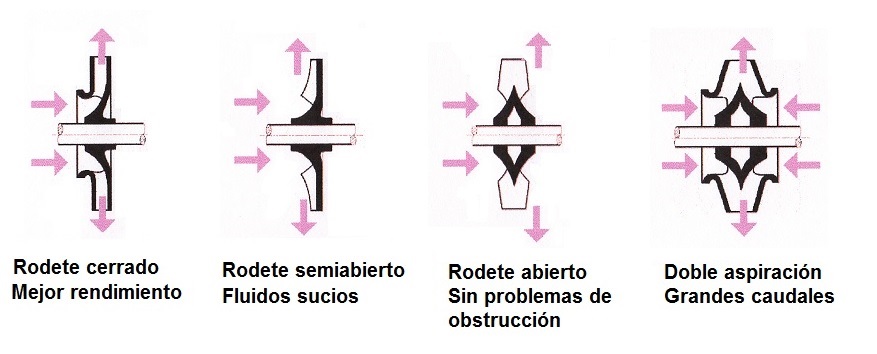
Figura 3. Tipologías de rodetes
Este tipo de máquinas generan un fluido continuo, empleándose para suministrar caudales altos con presiones moderadas.
En función de la trayectoria que sigue el fluido al ser lanzado por el rodete se distinguen varios tipos de bombas:
- Radiales o centrífugas: cuando el movimiento del fluido sigue una trayectoria perpendicular al eje del rodete impulsor.
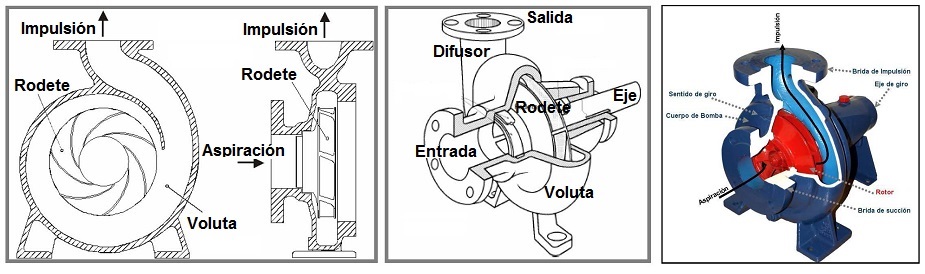
Figura 4. Bomba centrífuga. Esquema de funcionamiento
- Axiales: cuando el fluido pasa por los canales de los álabes siguiendo una trayectoria contenida en un cilindro. Empleada para mover grandes caudales de agua.
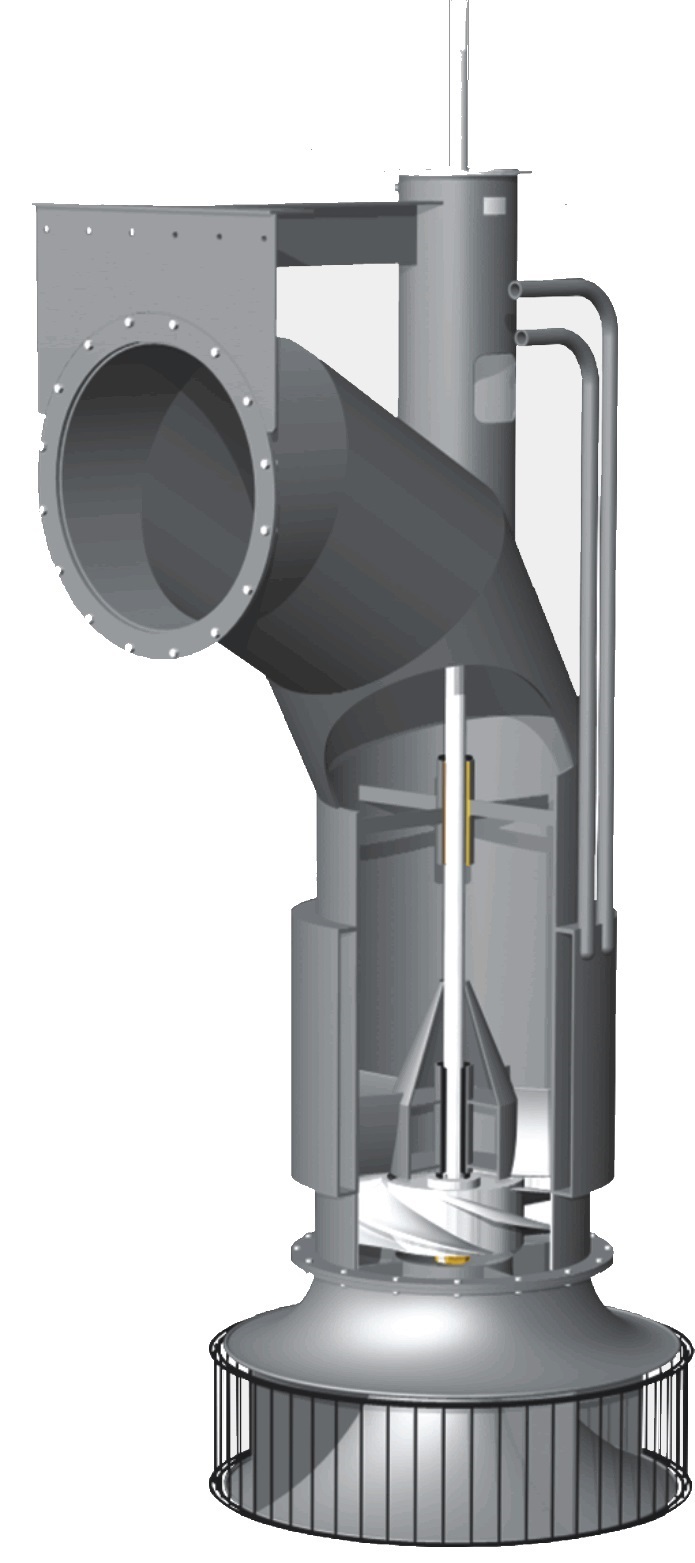
Figura 5. Bomba axial
- Diagonales o helicoidales: cuando la trayectoria del fluido se realiza en otra dirección comprendida entre las anteriores, es decir, en un cono coaxial con el eje del rodete.
2- Parámetros de funcionamiento
2.1- Potencia de la bomba
En un equipo de bombeo la potencia consumida por éste no es igual a la potencia que finalmente se transmite al fluido y que es la potencia útil realmente.
En efecto, la potencia teórica o potencia útil (Pu) que se transmite a un fluido, sea agua u otro cualquiera, y que se invierte en proporcionarle un caudal (Q) y altura manométrica (H) a su paso por el equipo de bombeo viene dado por la siguiente expresión:
Pu = ρ · g · Q · H
donde,
Pu, es la potencia proporcionada al fluido, en W;
Q, es el caudal de fluido que atraviesa la bomba, en m3/s;
H, es la altura manométrica ganada por el fluido a su paso por la bomba, en m;
ρ, es la densidad del fluido, en kg/m3;
g, es la aceleración de la gravedad: 9,81 m/s2.
Al producto (ρ · g) se denomina peso específico (γ), por lo que la expresión anterior quedaría como sigue:
Pu = γ · Q · H
siendo,
γ, el peso específico del fluido, en N/m3.
En la siguiente tabla se puede consultar, para el caso del agua, los valores del peso específico (γ en kg(fuerza)/dm3) y de la presión de vapor (Pv), también llamado tensión de vapor (Tv expresado en kg(fuerza)/cm2) para distintas temperaturas del agua:
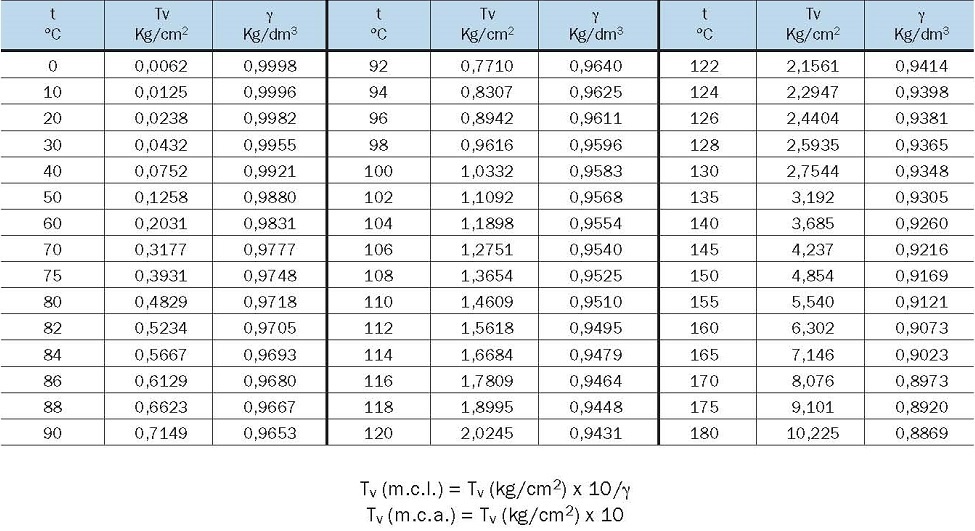
Tabla 1. Peso específico y tensión de vapor del agua
La potencia según calculada por la expresión anterior, es la potencia teórica o útil (Pu) que ganaría el fluido a su paso por el equipo de bombeo. No obstante, un equipo de bombeo está constituido, además de por la bomba propiamente, por un motor de accionamiento (que puede ser eléctrico o de combustión) acoplado mediante un eje a la bomba y de sistemas auxiliares.
La potencia finalmente consumida (Pe) por todo este equipo de bombeo es superior a la potencia útil (Pu), dado que habrá que considerar las pérdidas y rendimientos de cada uno de los componentes que intervienen.
Figura 6. Moto-bomba eléctrica
En efecto, en primer lugar se tiene la potencia que debe absorber el eje de la bomba (Pb), para suministrar el caudal (Q) y la altura manométrica (H), y cuyo valor es el proporcionado por las siguientes expresiones, según las unidades de medida empleadas:
|
γ · Q · H |
|
Pb (kW) = |
|
|
|
367 · ηH · ηV |
|
|
γ · Q · H |
|
Pb (CV) = |
|
|
|
270 · ηH · ηV |
|
|
γ · Q · H |
|
Pb (HP) = |
|
|
|
274 · ηH · ηV |
|
donde,
Q, es el caudal que impulsa la bomba, en m3/h;
H, es la altura manométrica ganada por el fluido a su paso por la bomba, en m;
γ, es el peso específico del fluido, en kg/dm3;
ηH, es el rendimiento hidráulico, expresado en porcentaje º/1;
ηV, es el rendimiento volumétrico, expresado en porcentaje º/1.
El rendimiento hidráulico (ηH) es un dato suministrado por el fabricante de la bomba, y con ello se tiene en cuenta las pérdidas de carga debido al rozamiento del fluido por las paredes de la bomba, válvulas y los rodetes. Sería igual al cociente entre la altura manométrica que realmente logra el fluido y la que lograría de no existir estas pérdidas.
El rendimiento hidráulico se puede estimar en los siguientes valores:
• entre 0,95 hasta 0,97 para bombas de gran tamaño y con unas condiciones de escurrimientos favorables;
• entre 0,85 hasta 0,88 para bombas más pequeñas y de diseño no demasiado elaborado.
El rendimiento volumétrico (ηV) es también un dato suministrado por el fabricante de la bomba, y con ello se tiene en cuenta las pérdidas por fugas de fluido dentro del cuerpo de la bomba.
El rendimiento volumétrico se puede estimar en los siguientes valores:
• entre 0,97 hasta 0,98 para bombas de cuidada ejecución y grandes caudales;
• entre 0,94 hasta 0,96 para bombas de cuidada ejecución y pequeños caudales;
• entre 0,89 hasta 0,92 para bombas de regular ejecución y pequeños caudales.
El rendimiento volumétrico está muy condicionado por la temperatura a la que circula el fluido por el interior de la bomba (dado que la temperatura influye en las holguras entre las piezas de la bomba y por tanto en la fuga del fluido, y sobre todo, en su grado de viscosidad). Para temperaturas muy altas el rendimiento volumétrico puede bajar hasta 0,65 ó 0,70.
Asimismo, las fugas y por ende, el rendimiento volumétrico, depende de la presión de trabajo de la bomba. Al aumentar la presión, aumentan las fugas y por tanto disminuye el rendimiento volumétrico de la bomba.
Por lo tanto, y una vez tenida en cuenta las pérdidas anteriores que reducen la eficiencia en una bomba, la relación entre la potencia útil (Pu) transmitida al fluido y la que debe recibir la bomba en su eje de entrada de accionamiento (Pb), es la siguiente en función de cada uno de los rendimientos anteriores:
Pu = Pb · ηH · ηV
donde,
(ηH) y (ηV) son los rendimiento hidráulicos y volumétricos respectivamente de la bomba.
En otro orden de cosas, y en el caso específico de una bomba de agua accionada por un motor eléctrico, la potencia eléctrica consumida de la red (Pe) o potencia activa es la que realmente interesa conocer porque expresa el consumo y condiciona el diseño de la instalación. Esta potencia viene expresada según las siguientes formulaciones:
- Para motores monofásicos:
|
U · I · cosφ |
|
Pe (kW) = |
|
|
|
1000 |
|
- Para motores trifásicos:
|
√3 · U · I · cosφ |
|
Pe (kW) = |
|
|
|
1000 |
|
donde,
U, es la tensión de servicio de la red eléctrica, en voltios (V);
I, es el consumo de corriente en el estátor, en amperios (A);
cosφ, es el factor de potencia.
Sin embargo, la potencia ofrecida por el motor eléctrico (Pm) en la salida de eje es menor que la potencia eléctrica consumida (Pe), debido a las pérdidas mecánicas que se producen en los órganos de transmisión del motor. De esta manera se obtiene que:
Pm (kW) = Pe · ηM
donde (ηM) es el rendimiento mecánico del motor que tiene en cuenta las pérdidas mecánicas debido al rozamiento en los cojinetes de los ejes, de las pérdidas en los órganos de comando y transmisión, etc.
El rendimiento mecánico se puede estimar en los siguientes valores:
• entre 0,94 hasta 0,96 para bombas directamente acopladas al eje motor, de gran caudal y diseño y mantenimiento cuidado;
• entre 0,83 hasta 0,86 para bombas pequeñas y con transmisión por correas o engranajes entre bomba y motor.
Finalmente, y considerando todas las anteriores pérdidas, la relación entre la potencia útil (Pu) transmitida al fluido y el total de potencia consumida de la red eléctrica (Pe) por la bomba estarían relacionadas de la siguiente forma:
Pu = Pe · ηH · ηV· ηM = Pe · ηG
donde,
ηG = ηH · ηV· ηM
siendo (ηG) el rendimiento global del equipo de bombeo que incluye el efecto de los distintos rendimientos (hidráulico, volumétrico y mecánico) de cada uno de los componentes anteriores.
2.2- NPSH (ANPA)
También denominada ANPA, o altura neta positiva de aspiración (en inglés, NPSH Net Positive Suction Head) es un parámetro que define la diferencia entre la presión del líquido en el eje impulsor y su presión de vapor a la temperatura que se realiza el bombeo.
Se consideran dos tipos de NPSH:
- NPSH disponible (NPSHd): es un parámetro característico de cada instalación e independiente de la bomba empleada. La expresión que define el NPSH disponible es la siguiente, obtenida a partir de aplicar el principio de conservación de la energía entre la superficie libre del líquido y el punto de aspiración:
NPSHd = (10 · Pa) / γ - Ha - Pca - (10 · Pv) / γ
donde,
Pa, es la presión atmosférica o presión en el depósito de aspiración, en kg/cm2;
Ha, es la altura geométrica de aspiración, en metros;
Pca, es la pérdida de carga originada en la aspiración (incluye todos los elementos que componen el circuito de aspiración: tuberías, válvulas, curvas, accesorios, etc.), en metros;
Pv, es la presión de vapor del líquido a la temperatura de bombeo, en kg/cm2;
γ, es el peso específico del líquido, en kg/dm3.
La presión atmosférica (Pa) que se tiene en la superficie del agua del depósito de aspiración, para aquellos depósitos abiertos a la atmósfera, como puedan ser pozos, embalses de agua, piscinas, etc. es variable con la altura topográfica que tiene el terreno sobre la que se asienta el depósito. El efecto de la presión atmosférica (Pa) con la altitud se puede determinar con la siguiente expresión:
Pa (m) = 10,33 - Altitud (m) / 900
- NPSH requerido (NPSHr): es un parámetro característico del tipo de bomba empleada, siendo un dato que suministra el fabricante de la bomba. La expresión que define el NPSH requerido es la siguiente,
|
va2 |
|
NPSHr = Hz + |
|
|
|
2 · g |
|
donde,
Hz, representa la presión mínima necesaria en la zona inmediatamente anterior a los álabes del rodete de la bomba, en metros;
va, es la velocidad de entrada del líquido en la bomba, en m/s. La expresión va2 / 2g representa la altura dinámica (presión) que tiene el líquido a la entrada de la bomba, en metros.
La importancia de conocer estos parámetros es vital para asegurar el correcto funcionamiento de la bomba y que permite identificar el problema más crítico que pueda surgir en el normal funcionamiento de una bomba, que es la cavitación, o formación de burbujas en la aspiración.
En efecto, una bomba de agua funciona creando una bajada de presión (el vacío) en la entrada del rodete que permite succionar el agua e impulsarla hacia la salida. Esta bajada de presión que se origina en la aspiración de la bomba tiene un límite, y este límite lo marca la presión de vapor del líquido, en este caso del agua, a la temperatura a la que se encuentra el propio líquido durante el bombeo.
Por otro lado, si el vacío que se origina en la aspiración de la |
bomba de vacío |
es tal que queda por debajo de la presión de vapor |
del agua, entonces ésta se evapora, creándose burbujas de vapor que dificultan la entrada a la bomba |
||
Además, estas burbujas cuando colapsan generan picos de presión que ocasionan picaduras en los álabes del rodete, además de vibraciones y ruidos que acaban ocasionando graves daños mecánicos en la bomba. Por ello es de vital importancia evitar que se puedan producir fenómenos de cavitación en la aspiración de la bomba.
Pues bien, existe una relación que asegura que una bomba funcione correctamente sin que surjan estos problemas de cavitación. Para ello es necesario que el NPSH disponible de la instalación sea mayor que su NPSH requerido en todo el rango de funcionamiento de la bomba. Si se incluye un margen de seguridad de 0,5 metros al NPSH requerido, la condición de no cavitación sería la siguiente:
NPSHd ≥ NPSHr + 0,5 m.
2.3- Diseño de la aspiración
En esta sección se expondrán algunas recomendaciones para la zona de aspiración de la bomba con objeto de maximizar sus prestaciones. En general, y como regla de buena práctica se recomienda que:
• Limitar en lo posible en el tramo de aspiración la presencia de codos, cambios de dirección, válvulas y accesorios;
• Realizar la impulsión hacia arriba que facilite la salida del aire;
• Colocar uniones flexibles para evitar la propagación de vibraciones;
• Disponer de válvula de retención o válvula de pie en la tubería de aspiración para evitar su vaciado cuando se detenga la bomba.
Un importante aspecto es evitar a toda costa la formación de turbulencias y torbellinos cercanos a la aspiración de la bomba, dado que pueden desencadenar la entrada de burbujas de aire por la aspiración.
Para asegurar que esto se cumpla se recomienda respetar las profundidades mínimas, indicadas en la tabla siguiente, a la que debe estar sumergida la boca de entrada de la tubería de aspiración respecto a la superficie del agua, según la velocidad que toma el agua por el conducto de aspiración.
Tabla 2. Profundidad mínima sumergida de la boca de aspiración |
|
Velocidad (m/s) |
Sumergencia (m) |
0,6 |
0,30 |
1,5 |
0,60 |
2,1 |
0,90 |
3,3 |
2,10 |
4,5 |
4,20 |
En otras ocasiones, ocurre que el diámetro de la tubería de aspiración es mayor que el de la brida de entrada a la bomba. Entonces se hace necesario el empleo de unos accesorios consistentes en conos difusores que adapten de manera gradual la diferencia de diámetros.
Estos conos, si son excéntricos, deben situarse tal que el lado recto quede por la parte superior de la tubería, salvo cuando la tubería de aspiración venga por arriba de la bomba, según se muestra en la figura siguiente.
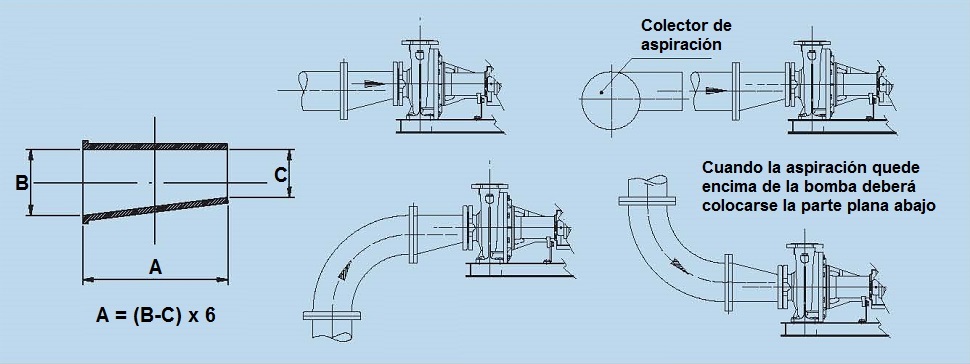
Figura 7. Colocación del cono difusor
3- Procedimiento de cálculo
3.1- Diámetro de tubería
La elección del diámetro de las tuberías de la instalación debe realizarse con el objetivo de limitar en lo posible las pérdidas de carga originadas por el rozamiento del flujo de agua con las paredes interiores de la tubería.
No obstante, debe llegarse a una solución de compromiso que haga económicamente rentable la instalación, dado que a mayor diámetro mayor es también el costo de la tubería.
Por otro lado, los diámetros de embocadura de las bridas en los orificios de aspiración e impulsión de la bomba, sólo determinan el diámetro mínimo que ha de tener las tuberías de la instalación, pudiéndose emplear accesorios (conos difusores) que acoplen el agarre a la bomba con el diámetro que finalmente resulte de la tubería.
El dimensionado final de los diámetros de las tuberías debe ser tal que las velocidades alcanzadas por el agua en el interior de las tuberías sean como máximo:
• Tubería de aspiración: 1,8 m/s;
• Tubería de impulsión: 2,5 m/s.
Velocidades del agua por el interior de los conductos inferiores a 0,5 m/s podría originar problemas de sedimentación, mientras que velocidades superiores a los 5 m/s podría originar fenómenos abrasivos en las paredes interiores de las tuberías que afectarían a su durabilidad.
La expresión que relaciona la velocidad del fluido (v) con el gasto o caudal (Q) es la siguiente:
Q = v · A
donde,
Q es el caudal volumétrico o flujo de agua que circula por la tubería;
v es la velocidad del agua en el interior de la tubería;
A es el área de la sección interna de la tubería (π·D2 / 4), siendo D el diámetro interior de la tubería.
Por lo tanto, sustituyendo y despejando (v) de la expresión anterior, el valor de la velocidad (v) del agua que discurre por el interior de una tubería también puede ser expresada en función del caudal (Q) y del diámetro interior (D) de la tubería, como:
v = |
Q |
A |
o bien,
v = |
4·Q |
π·D2 |
La expresión anterior toma las siguientes formas en función del sistema de unidades empleados para medir el caudal:
v = |
354·Q |
D2 |
o bien,
v = |
21,22·q |
D2 |
siendo,
v, la velocidad del agua, en m/s;
D, es el diámetro interior de la tubería, en mm;
Q, es el caudal de agua que circula por la tubería, en m3/h;
q, es el caudal de agua, pero expresado en l/min.
La manera de proceder para calcular el diámetro de la tubería sería la siguiente:
- El caudal de agua (Q, o bien, q) a suministrar por la bomba es un dato de partida y conocido, según las necesidades de la instalación que se desee proyectar.
- De un catálogo de fabricante de tuberías se selecciona el material y un diámetro de tubería.
- Haciendo uso de las expresiones anteriores, se calcula la velocidad de circulación del agua de manera iterativa con sucesivos diámetros hasta que finalmente resulte una velocidad cercana al rango recomendado anteriormente para las velocidades de las tuberías de aspiración e impulsión.
Se adjuntan los siguientes enlaces que muestran los diferentes diámetros comerciales de tuberías aptas para el bombeo de agua:
>> Catálogo de Tuberías de Polietileno (PE)
>> Catálogo de Tuberías de Polipropileno (PP-R)
>> Catálogos de Tuberías de Acero Negro Galvanizado
>> Catálogos de Tuberías de Fundición
>> Tuberías y Accesorios de PVC
3.2- Altura manométrica
El procedimiento de cálculo de una instalación de bombeo de agua comienza por el cálculo de la altura manométrica (H) ganada por el fluido y que debe ser proporcionada por la bomba, representando la resistencia que debe vencer el fluido desde el lugar de aspiración hasta la impulsión. Es conocida también como la presión que debe dar la bomba.
La altura manométrica en hidráulica se mide en metros, existiendo las siguientes correlaciones entre las distintas unidades de medida:
1 atmósfera = 1,033 kg/cm2 = 1,013 bar = 1,013·105 Pascal (Pa) = 10,33 metros de columna de agua (m.c.a.)
La altura manométrica (H) total se compone de la suma de los siguientes términos:
H = Hg + Pc + 10 · |
Pi - Pa |
γ |
donde,
Hg, representa a la altura geométrica que debe vencer el fluido, en metros;
Pc, es la pérdida de carga del fluido a su paso por las tuberías, válvulas, etc. y expresado en metros;
Pi - Pa / γ, este término representa la presión diferencial existente entre las superficies del líquido en la impulsión y la aspiración de la bomba, dividido por su peso específico. El resultado se expresa en metros. Para los casos comunes donde los lugares desde donde se realice la aspiración y la impulsión estén abierto a la atmósfera, las presiones de aspiración e impulsión en la superficie del líquido serán iguales (Pa = Pi) y por lo tanto esta componente resultará cero (Pa - Pi = 0) y no deberá ser tenida en cuenta.
- La altura geométrica (Hg) será la que resulte de sumar la altura de aspiración (Ha) y la altura de impulsión (Hi):
Hg = Ha + Hi
La altura de aspiración (Ha) es la altura geométrica medida desde el nivel mínimo del agua hasta el eje de la bomba, mientras que la altura de impulsión (Hi) es la altura geométrica medida desde el eje de la bomba hasta el nivel máximo de elevación.
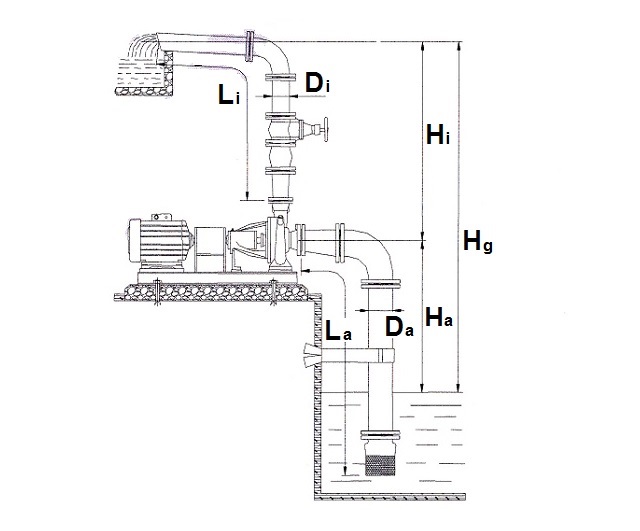
Figura 8. Altura geométrica
- El cálculo de la pérdida de carga (Pc) originada por el rozamiento al paso de los fluidos por las tuberías, válvulas y demás accesorios es un tanto complejo. El tutorial nº 208 "Cálculo y Diseño de Instalaciones de Fontanería", en su apartado 3.1 Cálculo de las pérdidas de carga, analiza el procedimiento para calcular la pérdida de carga en instalaciones de tuberías para distribución de agua.
No obstante, se va a proponer en esta sección algunos procedimientos más simplificados y rápidos, que permitirán estimar las pérdidas de carga que se originan en una instalación de bombeo de agua.
Por ejemplo, se adjunta el siguiente enlace donde están tabuladas las pérdidas de carga por rozamiento, expresadas en metros, para tramos rectos de tuberías de 100 metros de longitud, en función del caudal que circula y su diámetro interior:
Tabla de pérdidas de carga (Tuberías de PVC/Polietileno)
En esta otra tabla, se incluye un ábaco que permite estimar las pérdidas de carga por rozamiento, expresadas en metros, para tramos rectos de tuberías de hierro fundido:
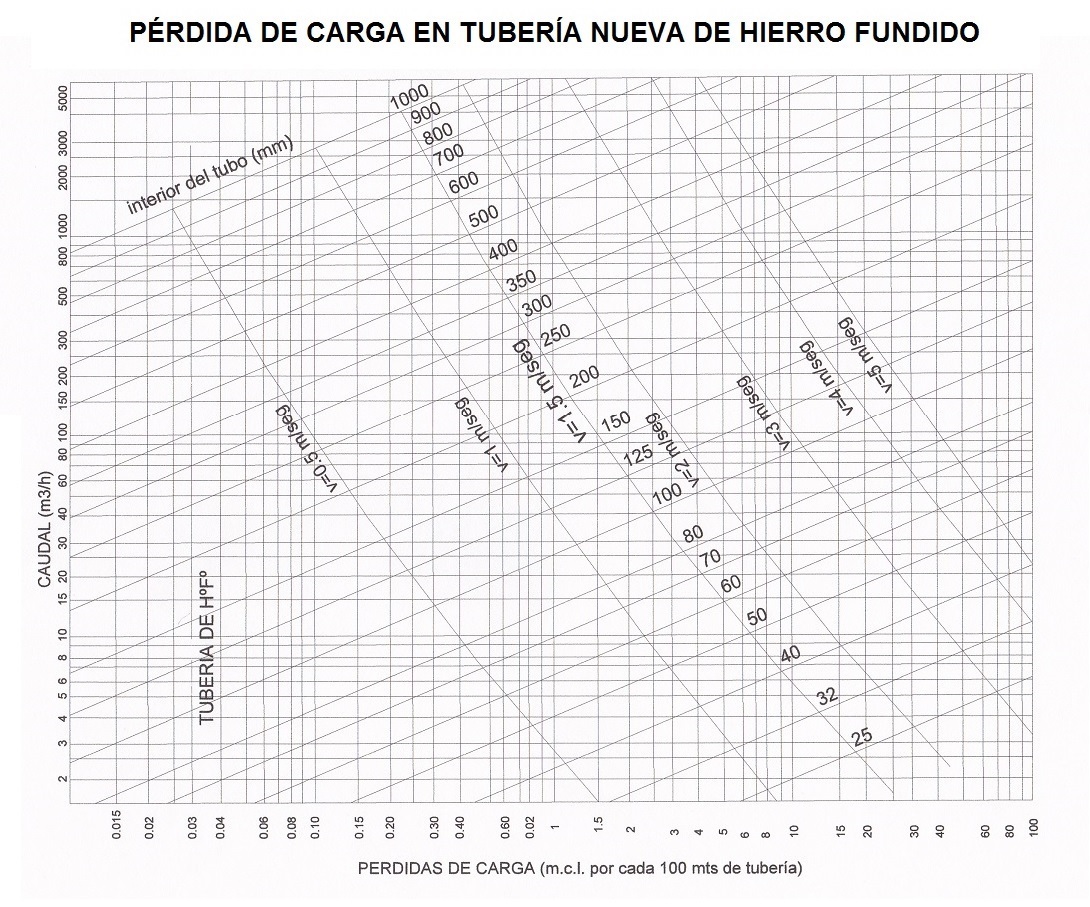
Tabla 3. Pérdidas de carga en tuberías de hierro fundido
Para tuberías fabricadas de otros materiales, se debe multiplicar el valor obtenido del ábaco anterior por los coeficientes correctores siguientes:
Tabla 4. Factores de corrección para pérdidas de carga |
|
Tipo de tubería |
Coeficiente corrector |
Hierro forjado |
0,76 |
Acero sin soldadura |
0,76 |
Fibro-cemento |
0,80 |
Cemento de paredes lisas |
0,80 |
Gres |
1,17 |
Hierro Forjado muy usada |
2,10 |
Hierro de paredes rugosas |
3,60 |
Por último, para estimar la pérdida de carga que se origina en elementos accesorios de la instalación (válvulas, codos, curvas, difusores...), se sustituye cada elemento por una longitud de tubería recta equivalente, que origina la misma pérdida de carga que el elemento en cuestión.
En la siguiente tabla se incluye la longitud equivalente de tubería en metros, para estimar la pérdida de carga en accesorios, según el tipo de accesorio y el diámetro del tubo donde va acoplado:
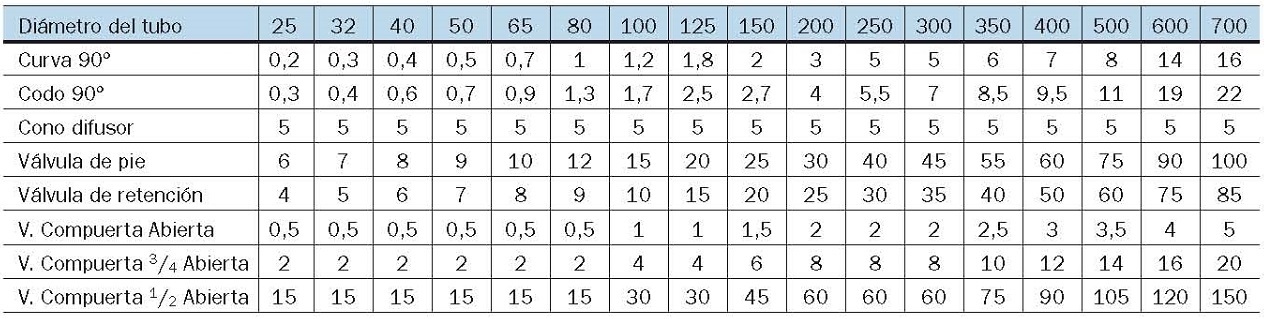
Tabla 5. Pérdidas de carga en accesorios
3.3- Elección del tipo de bomba
Una vez definido el caudal y altura manométrica que debe suministrar la bomba, cada fabricante de bombas dispone de una tabla de selección rápida que permite obtener el modelo que mejores prestaciones ofrece de entre toda la gama de bombas que presenta.
En la siguiente figura, se adjunta una tabla de selección tipo dado por un fabricante de bombas y donde se indican, según la dimensión del rodete y la boca de descarga, las zonas donde presentan mejores rendimientos cada modelo de bomba:
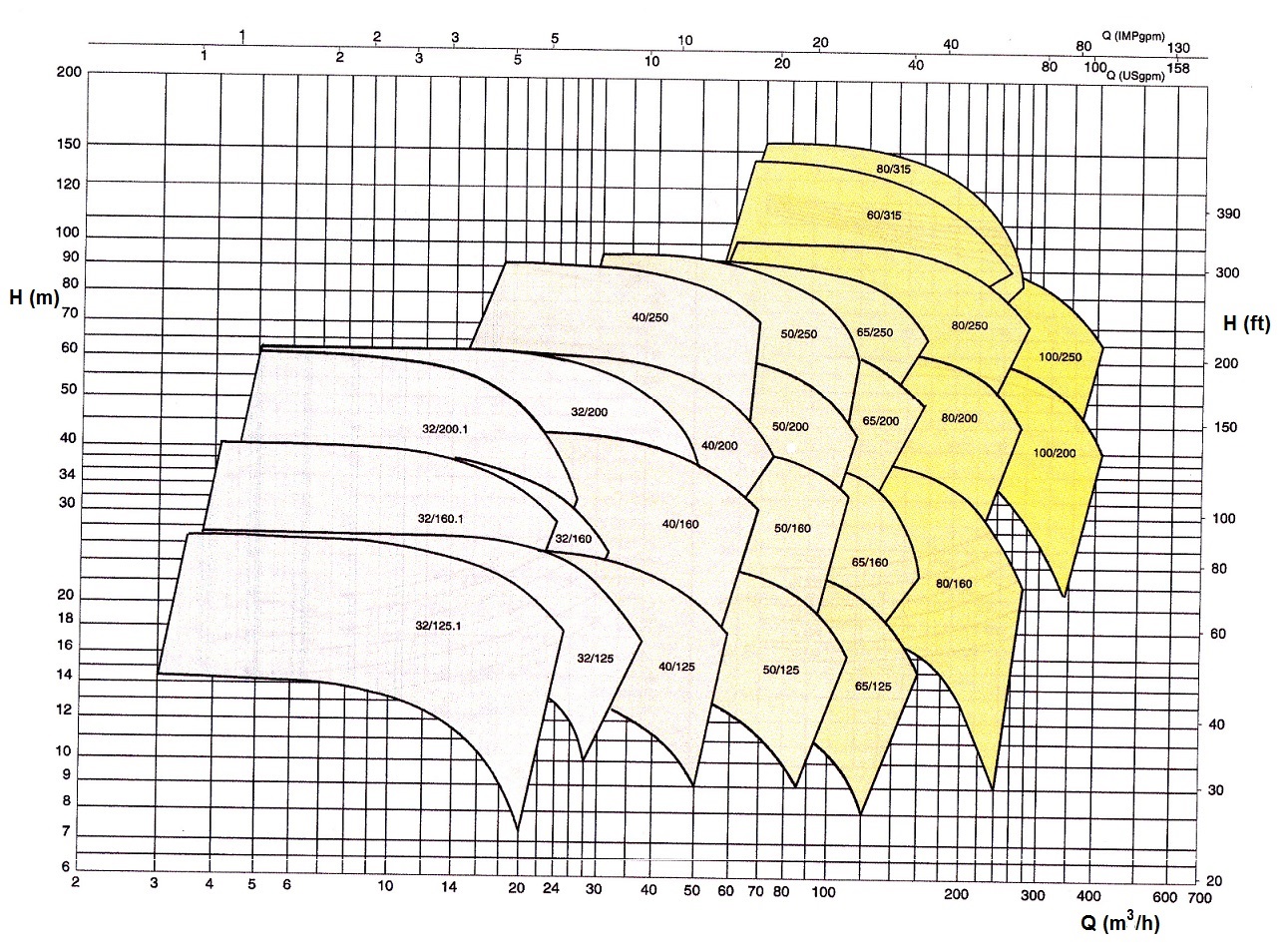
Tabla 6. Tabla de selección rápida de bombas
En general, para caudales de suministro pequeños y grandes alturas, la geometría radial es la que mejor rendimiento ofrece. Por el contrario, para suministrar grandes caudales y alturas limitadas, la geometría axial es la más eficiente. Y si se quiere proporcionar gran altura con un caudal moderado, son las bombas centrífugas las más recomendables.
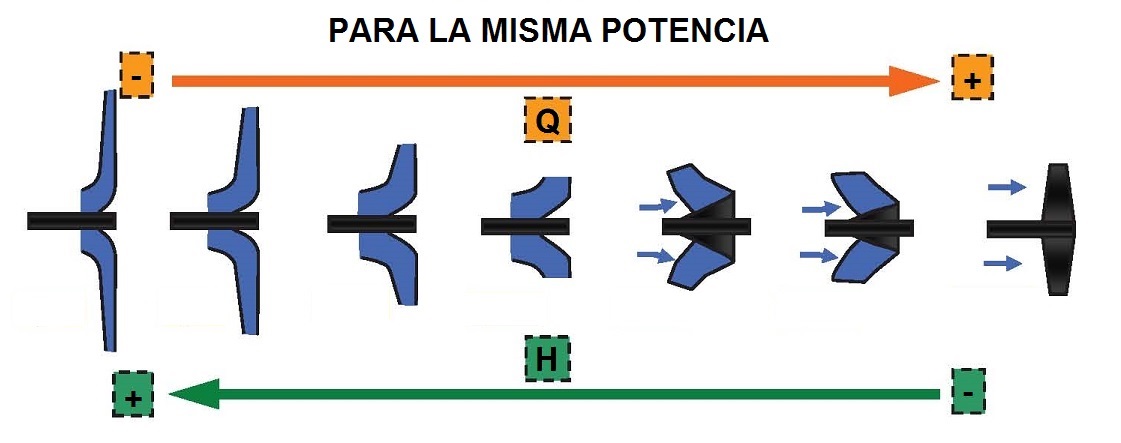
Figura 9. Selección de bombas en función del caudal y altura
3.4- Comprobación de ausencia de cavitación
La cavitación, como ya se vio en apartados anteriores, es un proceso de formación y posterior colapso de burbujas de vapor de agua en el seno de la corriente bombeada, que se forma en la aspiración, justo a la entrada del rodete, que es el punto de mínima presión.
Se produce cuando la presión en algún punto de la corriente de agua desciende por debajo de su presión de saturación a la temperatura a la que está el agua dentro de la bomba.
Pues bien, existe una relación que asegura que una bomba funcione correctamente sin que surjan estos problemas de cavitación. Para ello es necesario que el NPSH disponible de la instalación sea mayor que el NPSH requerido de la bomba. Si se incluye un margen de seguridad de 0,5 metros al NPSH requerido, la condición que habrá que comprobar que se cumple sería la siguiente:
NPSHd ≥ NPSHr + 0,5 m.
4- Ejemplo de cálculo
Se trata de calcular una instalación de bombeo para suministrar un caudal de 50 m3/h de agua, desde un pozo cuyo nivel de agua se encuentra a 4 metros por debajo de la cota de terreno, hasta un depósito de almacenamiento de agua cuyo borde superior se encuentra a un desnivel de +12 metros respecto a la cota de referencia de emplazamiento del eje de la bomba en el borde del pozo.

Por otro lado, el terreno donde se sitúa el pozo está a una altitud topográfica de unos 400 m sobre el nivel del mar.
Asimismo, las características de las líneas de aspiración e impulsión son las siguientes:
- Tubería de aspiración:
• Longitud: 8 metros;
• Válvula a pie de tubería: 1 ud;
• Codos a 90º: 1 ud;
• Cono difusor entrada a la bomba: 1 ud.
- Tubería de impulsión:
• Longitud: 50 metros;
• Válvula de retención: 1 ud;
• Válvula de compuerta: 1 ud;
• Codos a 90º: 3 uds;
• Cono difusor salida de la bomba: 1 ud.
Una vez definido los datos de partidas, se procede a calcular la instalación de bombeo, esto es, a decidir el tipo y modelo de bomba y los diámetros y tipos de tuberías para la conducción del agua.
1) Cálculo de los diámetros:
Según el apartado 3.1 de este tutorial, la expresión que relaciona el diámetro interior de la tubería con el caudal que la atraviesa es la siguiente:
v = |
354·Q |
D2 |
siendo,
v, la velocidad del agua, en m/s;
D, es el diámetro interior de la tubería, en mm;
Q, es el caudal de agua que circula por la tubería, en m3/h.
Expresión que permite despejar el diámetro (D) en función de la velocidad del agua (v) y el caudal de suministro (Q).
a) Diámetro tubería de aspiración:
En el mismo apartado 3.1 se recomendaba que para las tuberías de aspiración la velocidad del agua debería situarse en torno a los 1,8 m/s. Aplicando este valor y el caudal de 50 m3/h requerido a la expresión resulta el siguiente diámetro mínimo que se muestra en la siguiente tabla:
Velocidad (m/s) |
Caudal (m3/h) |
Diámetro (mm) |
1,8 |
50 |
99,16 |
Del catálogo de conductos de polietileno (PE) para suministro de agua a presión se elige para la tubería de aspiración la siguiente:
• Diámetro nominal (DN): 110 mm;
• Tipo: PE 40 (Tensión Mínima Requerida: 4 Mpa.)
• Espesor de pared del tubo: 4,2 mm;
• Diámetro libre interior: 101,6 mm.
Se adjunta para su consulta el enlace a dicho catálogo de tuberías de polietileno (PE):
Catálogo de tuberías de polietileno (PE)
Una vez definido el diámetro de la tubería de aspiración se recalcula la velocidad para obtener la real del agua y comprobar que se mantiene dentro del rango recomendado:
v = |
354·Q |
D2 |
siendo,
D, es el diámetro interior de la tubería: 101,6 mm;
Q, es el caudal de agua que circula por la tubería: 50 m3/h;
Sustituyendo resulta:
Diámetro (mm) |
Caudal (m3/h) |
Velocidad (m/s) |
101,6 |
50 |
1,7 |
Diseño conforme para la tubería de aspiración.
b) Diámetro tubería de impulsión:
Según el apartado 3.1 para las tuberías de impulsión se recomienda que la velocidad del agua debería situarse en torno a los 2,5 m/s. Aplicando este valor y el caudal de 50 m3/h, el diámetro mínimo resultante se muestra en la siguiente tabla:
Velocidad (m/s) |
Caudal (m3/h) |
Diámetro (mm) |
2,5 |
50 |
84,14 |
Del catálogo anterior de conductos de polietileno (PE) para suministro de agua a presión se elige para la tubería de impulsión la siguiente:
• Diámetro nominal (DN): 90 mm;
• Tipo: PE 40 (Tensión Mínima Requerida: 4 Mpa.)
• Espesor de pared del tubo: 3,5 mm;
• Diámetro libre interior: 83,0 mm.
Una vez definido el diámetro de la tubería para la impulsión se recalcula la velocidad real del agua, para comprobar que se mantiene dentro del rango recomendado:
v = |
354·Q |
D2 |
siendo,
D, es el diámetro interior de la tubería: 83,0 mm;
Q, es el caudal de agua que circula por la tubería: 50 m3/h;
Sustituyendo resulta:
Diámetro (mm) |
Caudal (m3/h) |
Velocidad (m/s) |
83,0 |
50 |
2,6 |
Diseño conforme.
2) Altura manométrica:
Según el apartado 3.2 de este tutorial, la altura manométrica (H) total se compone de la suma de los siguientes términos:
H = Hg + Pc + 10 · |
Pi - Pa |
γ |
donde,
Hg, representa a la altura geométrica que debe vencer el fluido, en metros;
Pc, es la pérdida de carga del fluido a su paso por las tuberías, válvulas, etc. y expresado en metros;
Pi - Pa / γ, este término representa la presión diferencial existente entre las superficies del líquido en la impulsión y la aspiración de la bomba, dividido por su peso específico. El resultado se expresa en metros. En este caso, al tratarse tanto el pozo donde se realiza la aspiración como el depósito final de impulsión de espacios abiertos a la atmósfera, resulta que las presiones de aspiración e impulsión en la superficie del líquido serán iguales (Pa = Pi) y por lo tanto esta componente resultará cero (Pa - Pi = 0) y no deberá ser tenida en cuenta.
Por lo tanto, para calcular la altura manométrica que debe proporcionar la bomba, habrá que calcular la altura geométrica que debe salvar el fluido en su recorrido y sumarle la pérdida de carga por rozamiento producida en la instalación. Se calculará en los tramos de aspiración e impulsión por separado y a continuación se sumarán para obtener la altura manométrica total.
a) Tubería de aspiración:
- Altura geométrica (Ha): 4 metros;
- Cálculo de la pérdida de carga (Pc):
Para calcular la pérdida de carga que se incurre en el tramo de aspiración se calculará su longitud equivalente (Leq,a), que incluye la longitud real más la correspondiente a los accesorios:
• Longitud de tubería en la aspiración: 8 metros;
• Longitud equivalente para válvula a pie de tubería (1 ud): 15 metros;
• Longitud equivalente para codos a 90º (1 ud): 1,7 metros;
• Longitud equivalente para cono difusor entrada a la bomba (1 ud): 5 metros.
Donde la longitud equivalente que corresponde a cada accesorio se ha obtenido de la Tabla 5 "Pérdidas de carga en accesorios" del apartado 3.2.
Sumando se obtiene una longitud equivalente para la tubería de aspiración de:
Leq,a = 29,7 m.
En el apartado 3.2 se incluye también el siguiente documento que permite calcular las pérdidas de carga, expresadas en metros, por cada 100 metros de tubería de polietileno, en función de su diámetro y caudal que circula:
Tabla de pérdidas de carga (Tuberías de PVC/Polietileno)
• Para el caso actual resulta:
Caudal (Q= 50 m3/h), diámetro (DN= 110 mm), interpolando en la tabla anterior resulta una pérdida de carga de: 1,8 metros/100 metros de tubería.
Como en este caso tenemos una Leq,a=29,7 metros, resulta una pérdida de carga en la aspiración de, Pc,a = 0,53 metros.
- Por lo tanto, la altura manométrica total en la aspiración (Haspiración) resulta de:
Haspiración = Ha + Pc,a = 4 + 0,53 = 4,53 m.
b) Tubería de impulsión:
- Altura geométrica (Hi): 12 metros;
- Pérdida de carga (Pc):
Para calcular la pérdida de carga que se incurre en el tramo de impulsión hasta el depósito final se calculará su longitud equivalente (Leq,i), que incluye la longitud real más la correspondiente a los accesorios:
• Longitud de tubería: 50 metros;
• Longitud equivalente para válvula de retención (1 ud): 9 metros;
• Longitud equivalente para válvula de compuerta (1 ud): 0,5 metros;
• Longitud equivalente para codos a 90º (3 uds): 1,3x3= 3,9 metros;
• Longitud equivalente para cono difusor salida de la bomba (1 ud): 5 metros.
De nuevo, la longitud equivalente que corresponde a cada accesorio se ha obtenido de la Tabla 5 "Pérdidas de carga en accesorios".
Sumando se obtiene una longitud equivalente para la tubería de impulsión de:
Leq,i = 68,4 m.
Del siguiente documento se extrae la pérdida de carga, expresadas en metros, por cada 100 metros de tubería de polietileno, en función de su diámetro y caudal que circula:
Tabla de pérdidas de carga (Tuberías de PVC/Polietileno)
• Para el caso actual resulta:
Caudal (Q= 50 m3/h), diámetro (DN= 90 mm), interpolando en la tabla anterior resulta una pérdida de carga de: 4,3 metros/100 metros de tubería.
Como en este caso tenemos una Leq,i= 68,4 metros, resulta una pérdida de carga en la impulsión de, Pc,i = 2,94 metros.
- La altura manométrica total en la tubería de impulsión (Himpulsión) resulta de:
Himpulsión = Hi + Pc,i = 12+ 2,94 = 14,94 m.
Por lo tanto, la altura geométrica total (H) que debe proporcionar la bomba será:
H = Haspiración + Himpulsión = 4,53 + 14,94 = 19,47 m.
En resumen, las condiciones de diseño de la bomba serán:
Condiciones de diseño para la bomba |
|
Caudal (m3/h) |
Altura manométrica (m) |
50 |
19,47 |
3) Elección del tipo de bomba:
Para la selección de la bomba, cada fabricante dispone de una tabla de selección rápida que permite obtener el modelo de bomba que mejores prestaciones ofrece de entre toda la gama de bombas que presenta. En estas tablas se entra con los valores de caudal y altura manométrica que debe ofrecer la bomba, y que han sido calculados previamente.
En este caso, se ha optado por seleccionar el equipo de bombeo del fabricante SACI pumps, de cuyos catálogos se puede extraer la siguiente tabla de selección rápida de bombas:
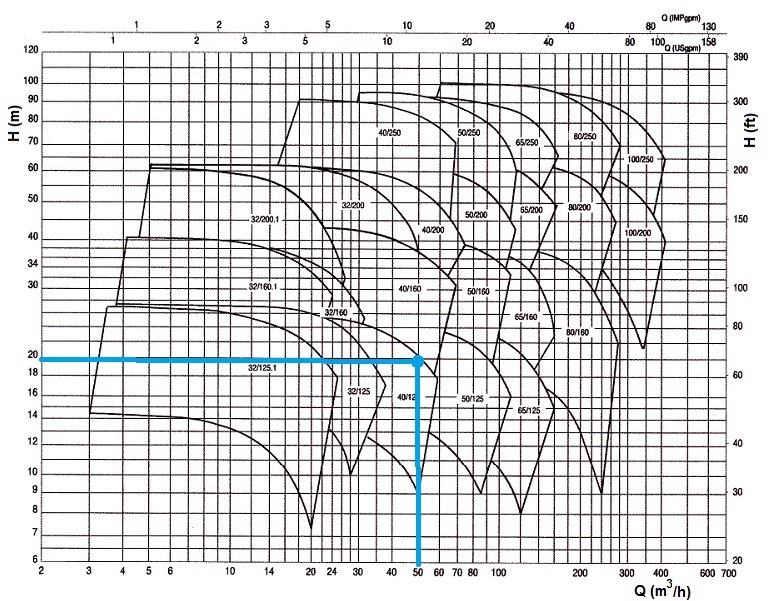
Tabla 7. Tabla de selección rápida de bombas
Como se muestra en la figura anterior, entrando en la tabla con un caudal (Q= 50 m3/h) y una altura manométrica (H= 19,47 metros) resulta adecuado el modelo KDN-40/125 de la gama de bombas del fabricante SACI.
A continuación se adjuntan también las tablas de funcionamiento de la bomba seleccionada:
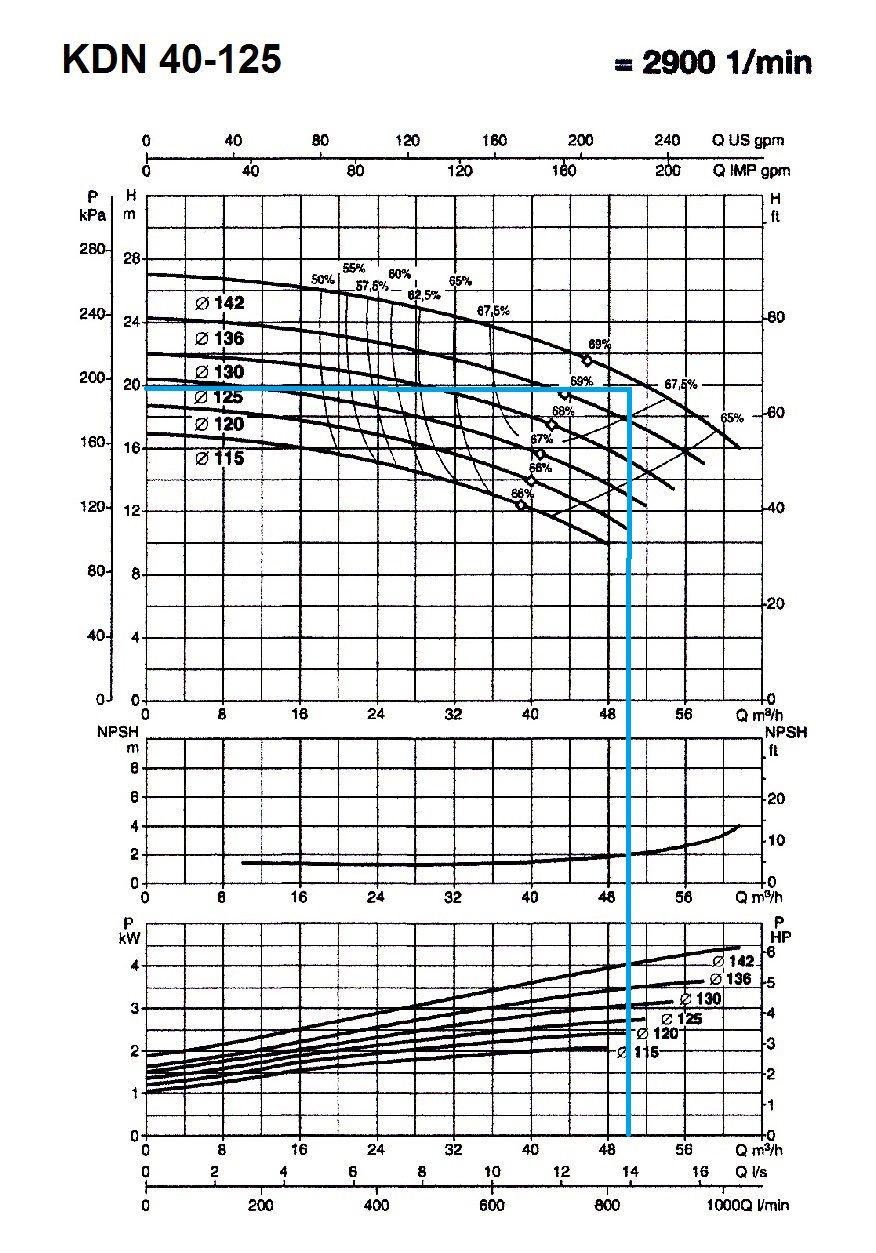
Tabla 8. Curvas de funcionamiento de la bomba KDN 40-125
La bomba seleccionada para este proyecto, se trata del modelo KDN 40-125/142, de la marca SACI pumps, con el cuerpo de la bomba, bancada de soporte y rodete de Ø142 mm en fundición de alta calidad, eje en acero inoxidable AISI-304, y sello mecánico en carbón-carburo de silicio con juntas tóricas EPDM. Dispone de motor eléctrico asíncrono normalizado, tipo cerrado y de ventilación externa, aislamiento clase F y grado de protección IP55, de 2 polos y 7,5 kW de potencia de consumo, voltaje 380/415 V a 50Hz.

Figura 11. Vista general de la moto-bomba seleccionada
4) Comprobación de ausencia de cavitación:
Según lo indicado en el apartado 3.4 de este tutorial, el equipo de bombeo funcionará correctamente sin que surjan problemas de cavitación, si se cumple que:
NPSHd ≥ NPSHr + 0,5 m.
- El NPSHr (requerido) de la bomba es un dato que se puede extraer del modelo seleccionado, a partir de la información facilitada por el fabricante en su catálogo.
De las curvas de funcionamiento anteriores (Tabla 8) se tiene que para la bomba seleccionada y el régimen de funcionamiento de diseño se obtiene el siguiente NPSH:
• NPSHr = 2,00 m.
- El NPSHd (disponible) de la instalación viene calculado según la expresión siguiente, ya vista en el apartado 2.2:
NPSHd = (10 · Pa) / γ - Ha - Pca - (10 · Pv) / γ
El emplazamiento de la bomba es en superficie sobre el terreno, a una altitud de 400 metros sobre el nivel del mar. A esta altitud la presión atmosférica se puede calcular como:
Pa(m) = 10,33 - Altitud(m)/900 = 10,33 - 400/900 = 9,89 m. (0,989 kg/cm2)
La altura geométrica de aspiración (Ha) vale 4 metros, según los datos de partida.
La pérdida de carga originada en el tramo de la aspiración (Pca) también ya ha sido calculada de valor, Pca= 0,53 metros.
Los otros parámetros de la expresión anterior que faltan toman los siguientes valores:
Pv= 0,0238 kg/cm2 (presión de vapor del agua a 20ºC, según la Tabla 1 "Peso específico y tensión de vapor del agua" del apartado 2.1);
γ= 0,9982 kg/dm3 (peso específico del agua a 20ºC, según la Tabla 1 "Peso específico y tensión de vapor del agua" del apartado 2.1);
Sustituyendo estos valores en la expresión anterior resulta un NPSH disponible de valor:
• NPSHd = 5,14 m.
Por lo tanto, se cumple que:
NPSHd ≥ NPSHr + 0,5 m.
5,14 ≥ 2,0 + 0,5 m.
No existiendo riesgo de cavitación.
ANEXOS
Anexo nº 1.- Catálogos de conductos y tuberías de agua
>> Catálogo de Tuberías de Polietileno (PE)
>> Catálogo de Tuberías de Polipropileno (PP-R)
>> Catálogos de Tuberías de Acero Negro Galvanizado
>> Catálogos de Tuberías de Fundición Dúctil
>> Tuberías y Accesorios de PVC
Anexo nº 2.- Catálogos de bombas de agua
>> Catálogos de bombas SACI
>> Catálogos de bombas WILO
>> FIN DEL TUTORIAL
Volver a
Tutoriales
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055


