— Tutorial nº 303 —
Capacidad de Tiro en los Tractores Agrícolas
Índice de contenidos:
1- Introducción
1.1- Generalidades
1.2- Definición del par motor
1.3- Definición de la potencia motor
2- Estudio de la cadena cinemática
2.1- Generalidades
2.2- Velocidad del tractor
2.3- Par y esfuerzo transmisible por las ruedas motrices
3- Capacidad de tracción
3.1- Generalidades
3.2- Cálculo del par de tiro en las ruedas motrices
3.3- Cálculo de la fuerza de tiro en las ruedas motrices
3.4- Influencia de la adherencia
3.5- Resistencia a la rodadura
Anexos:
Anexo 1- Caso práctico de cálculo de la capacidad de tracción de un tractor agrícola de 70 CV
Anexo 2- Fórmulas empíricas usadas en el cálculo de las prestaciones de los tractores agrícolas
DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Generalidades
En el mundo de los tractores agrícolas es de vital importancia para cualquier usuario poder conocer la capacidad que puede desarrollar el tractor para el desempeño de sus funciones como maquinaria agrícola.

Sin embargo, dependiendo del tipo de labor que vaya a desarrollar el tractor, esta potencia o capacidad del tractor se puede emplear de muy diversas formas, como por ejemplo:
- para tirar de aperos, arados o remolques;
- para el accionamiento de máquinas mediante el uso de la transmisión mecánica o "toma de fuerza" que dispone el tractor;
- funcionando como un motor hidráulico que sirva para accionar cilindros hidráulicos o máquinas que funcionen hidráulicamente.
El objetivo de este tutorial va a ser en concreto el estudio de la potencia de tracción, también llamada potencia de tiro o potencia a la barra, que es posiblemente el concepto que más puede interesar a los usuarios de tractores.
Como se verá en este tutorial, la potencia de tiro no va a depender sólo de la potencia efectiva que puede desarrollar el tractor, sino que va a estar condicionada en gran medida por el peso del lastre utilizado y de las condiciones de adherencia al suelo, que a su vez dependerá del estado de los neumáticos y del tipo y características del terreno sobre el que circula el tractor.
Por tanto, en los capítulos que sigue se va a realizar un análisis concreto de la capacidad de tiro de los tractores, que como se ha dicho, es posiblemente la característica que más pueda interesar a cualquier usuario de un tractor.
1.2- Definición del par motor
Previo al cálculo de la potencia de tiro de los tractores, es necesario comprender también el concepto de par motor que desarrolla los motores de los tractores agrícolas.
Como se sabe, en los cilindros del motor de cualquier tractor tiene lugar la combustión de la mezcla combustible-aire que genera un aumento de la presión y temperatura en el interior de los cilindros del motor.
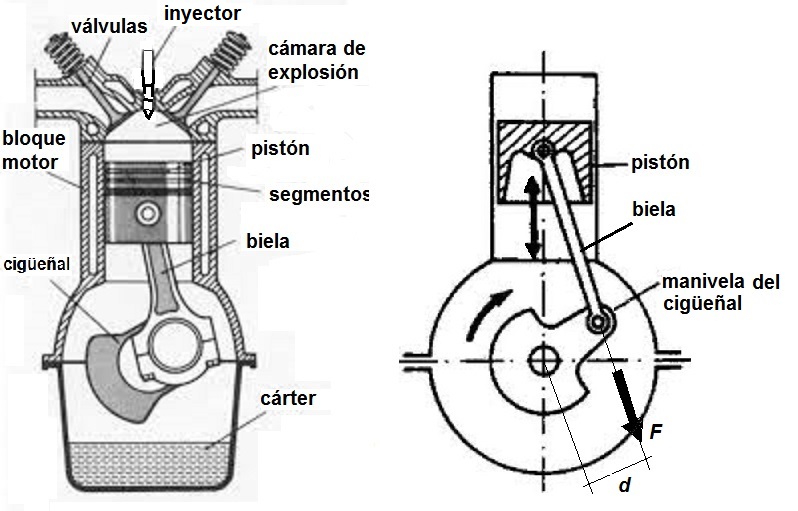
Esta presión interior produce a su vez una fuerza (F) de empuje sobre el pistón que lo desplaza generando el clásico mecanismo de biela-manivela de los motores de combustión interna alternativos, donde el movimiento de traslación del pistón en el interior del bloque motor se transforma en un movimiento circular de giro del cigüeñal.
Pues bien, el par motor o "torque" (T) es el producto de la fuerza aplicada (F) de empuje de los gases de combustión sobre los pistones por la distancia (d) al eje geométrico de giro del árbol del cigüeñal:
T = F · d
El par o torque motor se mide, según el Sistema Internacional de Unidades, en Newton metros (N·m).
En general, el par que puede ofrecer un motor de combustión depende del régimen de giro de funcionamiento del motor, y esta dependencia es mucho mayor en los motores de gasolina que en los diesel.
Así, si el motor funciona a bajas revoluciones, la combustión de la mezcla del combustible con el aire no resulta óptima debido a la escasa inercia que poseen los gases, que provoca que el llenado del cilindro no sea el óptimo, al igual que su vaciado, por lo que el par que puede ofrecer el motor resulta ser menor.
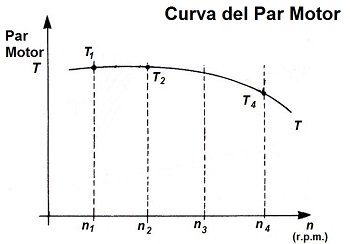
Y por otro lado, si el motor funciona a un elevado régimen de revoluciones, tampoco el llenado de los cilindros resulta completo, debido al escaso tiempo que dispone el gas para ocupar todo el recinto, de manera que la combustión en el interior de los cilindros tampoco resulta óptima, por lo que el par que puede ofrecer el motor también decrece.
En consecuencia, la franja de funcionamiento del motor donde logra entregar el máximo par es la zona central de revoluciones del motor. Esta dependencia de las revoluciones es más acusada en los motores de gasolina que en los motores diesel.
En efecto, en el caso de los motores diesel, que por otro lado es el tipo de motor que se emplea en los tractores agrícolas, la curva de par es prácticamente horizontal para un amplio rango de revoluciones del motor, incluso en niveles próximos al ralentí del motor.
Esto garantiza un buen par motor incluso a bajas revoluciones, lo cual resultará muy útil en situaciones difíciles, como pueda ser reanudar la marcha con el vehículo parado en una pendiente y sometido a carga.
Por eso se dice que los motores diesel son motores muy elásticos, es decir, presentan una curva del par motor con una gran zona plana en el centro que varía poco con las revoluciones del motor, por lo que resulta poca la necesidad de cambiar de marchas para adaptarse a los cambios de conducción.
Así, al poder ofrecer un par elevado en un amplio rango de revoluciones, los motores elásticos permiten acelerar con fuerza, incluso en marchas largas, sin tener que hacer uso del cambio de marchas. Gracias a ello, con este tipo de motores se puede circular empleando marchas más largas, revolucionando menos el motor y por tanto, mejorando el consumo.
1.3- Definición de la potencia motor
La potencia motor (P) que es desarrollada por el par motor (T) viene dada por la siguiente expresión:
P = T · ω
Siendo (ω) la velocidad angular de giro (rad/s) del eje de transmisión o eje del cigüeñal del motor.
La potencia motor (P) se mide, según el Sistema Internacional de Unidades, en watios (W), o kilowatios (1 kW = 1.000 W).
En ocasiones es interesante conocer la potencia en función de las revoluciones por minutos (r.p.m.) a la que gira el motor, en vez de la velocidad angular expresada en rad/s.
En efecto, si (n) son las revoluciones por minuto a la que gira el motor, entonces la potencia (P) se expresa como sigue,
|
T · n |
|
P = T · ω = |
|
|
|
60 / 2·π |
|
que aproximadamente resulta,
|
T · n |
|
P = |
|
|
|
9,55 |
|
donde,
P, es la potencia motor, en W
T, es el par motor, en N·m
n, son las revoluciones por minuto de giro del motor (r.p.m.)
En multitud de ocasiones, resulta útil conocer la potencia del motor expresada en otras unidades de uso muy común, como son: HP y CV.
- HP (Horse Power o caballo de potencia): es la unidad de medida de la potencia empleada en el sistema anglosajón de unidades, y se define como la potencia necesaria para levantar a la velocidad de 1 pie/minuto un peso de 32572 libras.
Sus equivalencias con otros sistemas son las siguientes:
• 1 HP = 745,69987 W
• 1 HP = 1,0139 CV
Por lo que la anterior expresión de la potencia (P) en función del par y las revoluciones del motor podría expresarse de la siguiente manera:
|
T · n |
|
PHP = |
|
|
|
7120,91 |
|
donde,
PHP, es la potencia motor, expresada en HP
T, es el par motor, en N·m
n, son las revoluciones por minuto de giro del motor (r.p.m.)
- CV (Caballo de Vapor): es la unidad de medida que emplea el sistema internacional (S.I.), y se define como la potencia necesaria para levantar un peso de 75 kg-fuerza (kgf) en un segundo, a un metro de altura.
Y sus equivalencias con otros sistemas son las siguientes:
• 1 CV = 735,49875 W
• 1 CV = 0,9863 HP
De manera que la potencia (P) expresada en CV, en función del par y las revoluciones del motor quedaría de la siguiente manera:
|
T · n |
|
PCV = |
|
|
|
7023,50 |
|
donde,
PCV, es la potencia motor, expresada en CV
T, es el par motor, en N·m
n, son las revoluciones por minuto de giro del motor (r.p.m.)
Por último, y en el caso que el par motor (T) estuviera expresado en kgf·m, entonces la expresión anterior que proporciona la potencia del motor (P) se expresaría como:
|
T · n |
|
PCV = |
|
|
|
716,2 |
|
donde,
PCV, es la potencia motor, expresada en CV
T, es el par motor, pero esta vez expresado en kgf·m
n, son las revoluciones por minuto de giro del motor (r.p.m.)
2- Estudio de la cadena cinemática
2.1- Generalidades
La cadena cinemática del tractor, al igual que la de cualquier vehículo, la constituye el conjunto de órganos y mecanismos encargado de transmitir el movimiento desde su generación (en el motor) hasta las ruedas motrices.
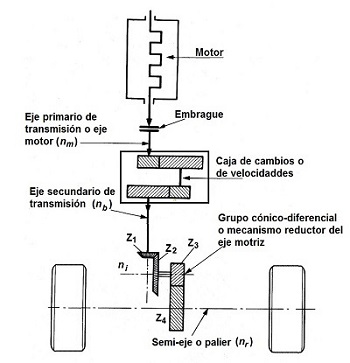
Dentro de los componentes que constituyen la cadena cinemática del tractor se pueden distinguir dos grandes grupos:
• el motor, que es el foco de generación del movimiento, y
• el sistema de transmisión, encargado de transmitir este movimiento desde su generación hasta su destino final en las ruedas motrices del vehículo.
A su vez, el sistema de transmisión de un tractor está compuesto por los siguientes órganos de transmisión del movimiento:
• embrague;
• caja de cambios de marchas;.
• ejes de transmisión, entre los cuales se distingue el eje primario que conecta la salida del embrague del motor con la entrada a la caja de velocidades, y el eje secundario de transmisión que conecta la salida de la caja de velocidades con la entrada al grupo cónico-diferencial instalado en el eje motriz;
• el grupo cónico-diferencial que es un mecanismo reductor instalado en el tren del eje motriz;
• los palieres o semiárboles que conectan el grupo diferencial con las ruedas motrices;
• las ruedas motrices.
2.2- Velocidad del tractor
En este apartado se va a detallar cómo calcular la velocidad (V) de marcha de un tractor, aunque puede ser aplicable a cualquier otro vehículo, en función del número de revoluciones de giro del motor (nm) y del diámetro de las ruedas motrices (D), para unos valores determinados de relaciones de transmisión de la cadena cinemática.
En efecto, si D es el diámetro de la rueda motriz y nr es la velocidad de giro del palier que conecta con la rueda, entonces se tiene que:
|
π · D · nr |
|
V = |
|
|
|
60 |
|
donde,
V es la velocidad de marcha del vehículo, en m/s;
D es el diámetro exterior de la rueda motriz, en m;
nr es la velocidad de giro del palier o rueda, en revoluciones por minuto (r.p.m.)
Por otro lado, si se llama rc a la relación de transmisión que se tenga en la caja de cambios de velocidades, se tendrá que:
|
nb |
|
rc = |
|
|
|
nm |
|
donde,
nb es la velocidad de giro del eje secundario a la salida de la caja de cambios, en r.p.m.
nm es la velocidad de giro del motor, en r.p.m.
Del mismo modo, para el eje motriz se tiene que la relación de transmisión rd que se obtiene en el grupo cónico-diferencial instalado en el eje motriz, se expresa como:
|
nr |
|
rd = |
|
|
|
nb |
|
donde,
nr es la velocidad de giro del palier, que es igual al de la rueda, a la salida del grupo cónico-diferencial, en r.p.m.
nb es la velocidad de giro del eje secundario a la salida de la caja de cambios y que conecta a su vez con el grupo cónico-diferencial del eje motriz, en r.p.m.
Multiplicando miembro a miembro las dos anteriores expresiones se tiene que:
|
nr |
|
rc · rd = |
|
|
|
nm |
|
Y por lo tanto,
nr = nm · rc · rd
Sustituyendo el anterior valor de nr en la expresión que proporciona la velocidad de marcha del vehículo (V) del comienzo de este apartado:
|
π · D · nr |
|
V (m/s) = |
|
|
|
60 |
|
Se tiene finalmente que,
|
π · D · nm · rc · rd |
|
V (m/s) = |
|
|
|
60 |
|
La anterior expresión proporciona el valor de la velocidad (V) en m/s. Si se prefiere la velocidad en kilómetros/hora (km/h) se tiene esta otra expresión:
|
3 · π · D · nm · rc · rd |
|
V (km/h) = |
|
|
|
50 |
|
Como se puede deducir de la anterior expresión, para valores fijos de rc y de rd, la velocidad del vehículo (V) dependerá del número de revoluciones del motor (nm) y del diámetro de la rueda motriz (D).
Y por otro lado, si se tienen los valores fijos de nm, D y rd , en este caso la velocidad del vehículo (V) dependerá de la relación de transmisión de la caja de cambios rc .
2.3- Par y esfuerzo transmisible por las ruedas motrices
Como ya se ha visto anteriormente, el sistema de transmisión de cualquier tractor, como de la mayoría de vehículos, está compuesto por los siguientes órganos principales:
• embrague;
• caja de cambios;
• ejes de transmisión;
• el grupo cónico-diferencial;
• los palieres que conectan a las ruedas motrices;
• las ruedas motrices.
Es evidente que en cada uno de los anteriores órganos que componen el sistema de transmisión de un tractor se producen pérdidas debidas al rozamiento entre piezas y a otras causas, que hace que la potencia final transmitida a las ruedas motrices (Pr) sea menor que la potencia generada en el motor (Pm).
En este sentido se define el rendimiento de la transmisión (ηt) a la relación entre la potencia finalmente transmitida por las ruedas motrices (Pr) y la potencia que transmite el motor (Pm). Es decir:
|
Pr |
|
ηt = |
|
|
|
Pm |
|
El rendimiento total de la cadena de transmisión (ηt) se obtiene a partir de los rendimientos de cada uno de los elementos y órganos que lo constituyen, desde el eje de salida del motor hasta el palier de la rueda, es decir, embrague, caja de cambios, ejes de transmisión, grupo cónico-diferencial, etc.:
ηt = η1 · η2 · ... · ηn
En la mayoría de los vehículos que dispongan de un sistema de transmisión clásica, este rendimiento (ηt) de la cadena de transmisión estará comprendido entre un 80 y un 90% (entre un 80-85% en velocidades cortas, y entre un 85-90% para velocidades largas).
Considerar un rendimiento medio para una transmisión del 85% (ηt = 0,85) suele ser una buena aproximación para la mayoría de los casos.
Por otro lado, del apartado 1.3 anterior se ha visto que la expresión que permite calcular la potencia entregada por el motor era la siguiente:
|
Tm · nm |
|
Pm = |
|
|
|
716,2 |
|
donde,
Pm es la potencia motor, expresada en CV
Tm es el par transmisible por el motor, en kgf·m
nm son las revoluciones por minuto de giro del motor (r.p.m.)
Y por otro lado, la potencia transmisible por las ruedas motrices (Pr), vendrá igualmente dada por esta otra expresión:
|
Tr · nr |
|
Pr = |
|
|
|
716,2 |
|
donde,
Pr es la potencia transmisible por las ruedas motrices, expresada en CV
Tr es el par transmisible por las ruedas motrices, en kgf·m
nr son las revoluciones por minuto de giro de las ruedas motrices (r.p.m.)
Teniendo en cuenta que el rendimiento de la transmisión (ηt) se expresa como:
|
Pr |
|
ηt = |
|
|
|
Pm |
|
sustituyendo los valores de Pm y de Pr , se tiene que:
|
Tr · nr |
|
ηt = |
|
|
|
Tm · nm |
|
Es decir, que el par transmisible por las ruedas motrices (Tr) se puede expresar como:
|
ηt · Tm · nm |
|
Tr = |
|
|
|
nr |
|
Pero como se vio en apartados anteriores, las revoluciones de giro de las ruedas motrices (nr) se podían expresar como:
nr = nm · rc · rd
Sustituyendo, resultará finalmente que el par transmisible (Tr) por las ruedas motrices de un tractor se podrá expresar como:
|
ηt · Tm |
|
Tr = |
|
|
|
rc · rd |
|
donde,
ηt es el rendimiento total de la transmisión del tractor
Tm es el par motor
rc es la relación de transmisión en la caja de cambios
rd es la relación de transmisión en el grupo cónico-diferencial del eje motriz.
Por último, conocido ya cómo calcular el par que transmite las ruedas motrices (Tr), se podría obtener también el esfuerzo tangencial (F) que transmite las ruedas motrices al suelo, que es el esfuerzo que hace avanzar al tractor.
En efecto, por definición física del par de fuerzas, se tiene que el esfuerzo tangencial (F) que realizan las ruedas motrices en el suelo en función del par se expresa como:
|
Tr |
|
F = |
|
|
|
D / 2 |
|
donde D es el diámetro exterior de las ruedas motrices.
Y sustituyendo la expresión del par de las ruedas motrices (Tr) en función del par motor (Tm), se tiene que el esfuerzo tangencial (F) que transmiten las ruedas motrices al suelo se calcula como:
|
2 · ηt · Tm |
|
F = |
|
|
|
D · rc · rd |
|
donde,
F es la fuerza motriz transmitida tangencialmente por el neumático del tractor al suelo
ηt es el rendimiento total de la transmisión del tractor
Tm es el par motor
rc es la relación de transmisión en la caja de cambios
rd es la relación de transmisión en el grupo cónico-diferencial del eje motriz
D es el diámetro de las ruedas motrices.
3- Capacidad de tracción
3.1- Generalidades
Las labores más habituales para las que se emplean los tractores agrícolas son para el arrastre de aperos, arados, remolques o máquinas agrícolas, por lo que se necesita disponer de una fuerza de tiro suficiente para cumplir con este objetivo.

Esta fuerza de tiro depende obviamente de la potencia que pueda desarrollar el motor del tractor, pero además se suele requerir de una cierta velocidad a la que se mueva el tractor para poder realizar sus funciones correctamente.
Según la definición como magnitud física, la potencia de tracción que se desarrolla en el tiro de un tractor (PT) es igual al producto de la fuerza que desarrolla por la velocidad a la que circula el tractor (PT = FT · V). Por tanto, para una misma cantidad de potencia, la fuerza de tiro (FT) que se puede desarrollar será mayor conforme la velocidad (V) a la que se mueve el conjunto sea menor.
- EJEMPLO DE CÁLCULO:
Como ejemplo de cálculo supongamos que para realizar el arrastre de un remolque se necesita ejercer una fuerza de tiro mínima en el enganche del tractor de 1.000 kilopondios (kp) o kilogramo-fuerza (kgf), a una velocidad sostenida del conjunto tractor + remolque de 20 km/h (5,5 m/s).
En primer lugar se expresa la fuerza de tiro necesaria en unidades del S.I.:
1.000 kp = 9.810 Newton (dado que 1 kp = 1 kgf = 9,81 N)
La potencia de tiro (PT) requerida que deberá desarrollar el tractor en el punto de enganche, para ejercer una fuerza de tiro mínima de 1.000 kgf a una velocidad sostenida de 20 km/h, deberá ser de:
PT = FT · V = 9810 · 5,5 = 53.955 W = 53,9 kW = 73,4 CV, dado que 1 CV = 735 Watios.
3.2- Cálculo del par de tiro en las ruedas motrices
La capacidad de tracción o de tiro de un tractor viene determinado por el par motor o torque (T) que puede desarrollar, valor que puede ser consultado en las especificaciones técnicas del vehículo que proporciona en los catálogos el fabricante del tractor.
No obstante, como se ha visto anteriormente, el par motor que sale por el cigüeñal del motor es modificado a través de los distintos órganos que conforma el sistema de transmisión del vehículo (caja de cambios, diferencial, reducciones finales en las ruedas, etc.), de manera que el par de tracción que se obtiene en las ruedas motrices del tractor es diferente, normalmente muy amplificado, al par motor que sale directamente del eje del motor.

Esta amplificación del par motor que finalmente se obtiene en las ruedas es debido a la disminución de la velocidad de giro que se produce en cada elemento que compone el sistema de transmisión del tractor.
Recordemos que la velocidad de giro y el par están inversamente relacionados, a partir de la expresión ya vista de: P = T · ω
De esta manera, para un determinado valor de la potencia (P), conforme se disminuye la velocidad de giro (ω) de un órgano de la transmisión, se produce un aumento en la misma proporción del par que se transmite (T), de manera que su producto siga siendo constante, e igual a la potencia (P) transmitida.
Como ya se ha visto en los apartados anteriores, la potencia de un motor (Pm) puede ser expresada en función del par motor o torque motor que desarrolla (Tm) y de la velocidad angular a la que gira el eje de salida del motor (ωm):
Pm = Tm · ωm
Por otro lado, el par final transmisible (Tr) por las ruedas motrices del tractor se podía expresar como:
|
ηt · Tm |
|
Tr = |
|
|
|
rc · rd |
|
donde,
ηt es el rendimiento total de la transmisión del tractor
Tm es el par motor
rc es la relación de transmisión en la caja de cambios
rd es la relación de transmisión en el grupo cónico-diferencial del eje motriz del tractor.
- EJEMPLO DE CÁLCULO:
Sea un tractor de 90 CV en cuyas especificaciones técnicas se indica que es capaz de desarrollar un par motor (Tm) de 280 N·m a un régimen de giro del motor de 1600 r.p.m.
Supongamos que el tractor trabaja en una marcha corta con una relación de transmisión total de 200:1 (es decir, 1 vuelta de la rueda motriz por cada 200 vueltas del volante del motor). Se trataría de calcular el par de tiro (Tr) que desarrolla el tractor en el eje motriz.
En primer lugar, se deben expresar todas las magnitudes en el mismo sistema de unidades, en este caso, en el Sistema Internacional (S.I.):
Par motor, Tm = 280 N·m
Revoluciones de giro del motor, ωm = 1600 r.p.m. = 167,5 rad/s
En este régimen de funcionamiento, la potencia (Pm) que desarrolla el motor del tractor será de:
Pm = Tm · ωm = 280 · 167,5 = 46.900 W (63,8 CV)
Como ya se sabe, en todo tractor se generan pérdidas a través de todos los órganos del sistema de transmisión que componen la cadena cinemática del tractor, de manera que no toda la potencia que genera el motor se transmite finalmente a las ruedas motrices del tractor.
Como ya se ha visto en los apartados anteriores, se define el rendimiento de la transmisión (ηt) a la relación entre la potencia finalmente transmitida por las ruedas motrices (Pr) y la potencia que genera el motor (Pm):
|
Pr |
|
ηt = |
|
|
|
Pm |
|
En la mayoría de los tractores que dispongan de un sistema de transmisión clásica, este rendimiento (ηt) de la cadena de transmisión estará comprendido entre un 80 y un 90%. Considerar un rendimiento medio para una transmisión del 85% (ηt = 0,85) suele ser una buena aproximación para la mayoría de los casos.
Por tanto, considerando un rendimiento de la transmisión de ηt = 0,85, la potencia transmitida a las ruedas es de:
Pr = Pm · ηt = 46.900 · 0,85 = 39.865 W
En este ejemplo de cálculo se ha supuesto que el tractor trabaja en una marcha corta con una relación de transmisión de 200:1, por lo que el régimen de giro de la rueda motriz del tractor es de:
Giro de la rueda motriz, ωr = ωm / 200 = 167,5 / 200 = 0,84 rad/s
Y por tanto, finalmente el par de tiro (Tr) que se desarrolla en la rueda matriz vale:
Tr = Pr / ωr = 39865 / 0,84 = 47.458 N·m
3.3- Cálculo de la fuerza de tiro en las ruedas motrices
Conocido el par que transmite las ruedas motrices (Tr), se podría obtener también el esfuerzo tangencial (F) que transmite las ruedas al suelo. Este esfuerzo es muy importante conocerlo porque nos proporcionaría finalmente la fuerza de tiro real del tractor.

Por definición del par de fuerzas, se tiene que el esfuerzo tangencial (F) que realiza cada rueda motriz en el suelo, viene expresado en función del par que desarrolla:
|
Tr |
|
F = |
|
|
|
D / 2 |
|
donde,
Tr es el par transmisible por las ruedas motrices del tractor
D es el diámetro exterior de la rueda motriz.
Por otro lado, según se ha visto en apartados anteriores, el par final transmisible (Tr) por las ruedas motrices del tractor se podía expresar en función del par motor como:
|
ηt · Tm |
|
Tr = |
|
|
|
rc · rd |
|
donde,
ηt es el rendimiento total de la transmisión del tractor
Tm es el par motor
rc es la relación de transmisión en la caja de cambios
rd es la relación de transmisión en el grupo cónico-diferencial del eje motriz del tractor.
Sustituyendo, se puede obtener el esfuerzo tangencial (F) que realiza cada rueda motriz en el suelo en su punto de apoyo en función del par motor (Tm) del tractor:
|
2 · ηt · Tm |
|
F = |
|
|
|
D · rc · rd |
|
donde,
F es la fuerza motriz tangencial transmitida por el neumático del tractor al suelo
ηt es el rendimiento total de la transmisión del tractor
Tm es el par motor
rc es la relación de transmisión en la caja de cambios
rd es la relación de transmisión en el grupo cónico-diferencial del eje motriz
D es el diámetro de las ruedas motrices.
Expresión que permite calcular finalmente la fuerza de tiro (F) que puede desarrollar el tractor en función del par motor, del diámetro de las ruedas motrices y de las relaciones de transmisión.
- EJEMPLO DE CÁLCULO:
Siguiendo con los cálculos del ejemplo del apartado anterior, el par de tiro calculado que desarrolla las ruedas matrices era de: Tr = 47.458 N·m, funcionando el motor a un régimen de 1.600 r.p.m.
Suponiendo que la rueda motriz del tractor tiene un diámetro D = 1600 mm., la fuerza de tiro que desarrollaría el tractor sería de:
|
Tr |
|
F = |
|
|
|
D / 2 |
|
Que sustituyendo valores, resulta finalmente una fuerza de tiro de:
F = 47458 / (0,8) = 59.322 N (6.047 kgf)
Esta fuerza es la que transmite la rueda motriz al suelo en su punto de apoyo y que el suelo debe resistir para permitir el avance del tractor, es decir, que cuando el suelo aguanta este esfuerzo tangencial el tractor podrá seguir tirando y avanzando con esta fuerza.
Sin embargo, cuando el suelo, por sus características o propiedades no aguanta este esfuerzo y se rompe, la rueda no podrá transmitir este esfuerzo en su totalidad al suelo y patinará, es decir, que girará pero sin que se produzca el avance del tractor. Por tanto, en estas condiciones el tractor no podrá desarrollar de forma útil toda la fuerza de tiro, porque el suelo no lo aguanta.
Cuando el suelo es una carretera asfaltada o adoquinada no habrá problema, porque tiene unas propiedades mecánicas suficientes para aguantar grandes esfuerzos tangenciales. Pero cuando se trata de tierras sueltas o de poca consistencia, la única forma de mejorar su resistencia es ofreciendo mayor superficie de contacto entre la rueda y el suelo, con lo que se consigue, para una misma fuerza de tiro, reducir la presión de contacto que transmite la rueda al suelo.
Por eso, para conseguir una mayor superficie de contacto entre rueda y suelo, y disminuir la presión de contacto, los neumáticos usados en tractores suelen disponer de relieves o tacos en su superficie de apoyo, lo que permite así aprovechar mejor la capacidad de tiro del tractor.
3.4- Influencia de la adherencia
El suelo, además de poder soportar el peso del tractor y los aperos que arrastre, debe soportar también la fuerza de tiro (F), calculada en el apartado anterior, que transmite las ruedas motrices al suelo para el avance del tractor.
Esta fuerza de tiro (F) actúa tangencialmente sobre el suelo, tendiendo a deformarlo. Si el suelo tiene la consistencia adecuada y no se rompe, podrá hacer frente a esta fuerza de tiro y hacer que el tractor avance.
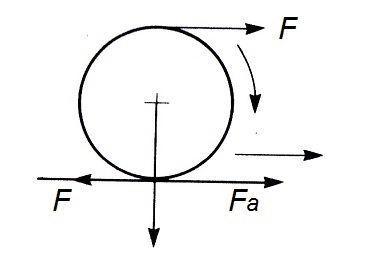
Si por el contrario el suelo no soporta adecuadamente esta fuerza tangencial y se rompe o se deforma en exceso, hará que las ruedas patinen y el tractor no avanzará, ni desarrollará toda la fuerza de tiro disponible.
Esta fuerza de adherencia (Fa), que se opone a la fuerza de tiro de la rueda, y que permite que gire la rueda sin patinar, permitiendo el avance del tractor, se puede calcular a partir de la siguiente relación:
Fa = µa · QT
siendo,
Fa la fuerza de adherencia entre el suelo y la rueda motriz
QT es el peso total que gravita sobre la rueda motriz del tractor
µa es un coeficiente adimensional, llamado coeficiente de adherencia.
El coeficiente de adherencia (µa) es un valor que se obtiene experimentalmente, pues depende tanto de la naturaleza del terreno o pavimento sobre el que circule el tractor, como del estado y naturaleza de los neumáticos del tractor
En la siguiente tabla se muestran valores para el coeficiente de adherencia (µa), considerándose para todos los casos que el tractor disponga de los neumáticos en buen estado:
Tabla 1. Valores para el coeficiente de adherencia (µa) |
|
Naturaleza y tipo de suelo |
Coeficiente de adherencia (µa) |
Suelo agrícola suelto |
0,48 |
Tierra labrada húmeda |
0,52 |
Tierra labrada seca |
0,57 |
Rastrojo seco |
0,60 |
Camino empedrado seco |
0,70 |
Carretera de cemento |
0,80 |
Carretera de asfalto seco |
0,60 a 0,75 |
Carretera húmeda |
0,30 a 0,40 |
Carretera mojada |
0,25 |
Carretera con hielo |
0,08 a 0,10 |
Como ya se ha explicado anteriormente, el motor del tractor desarrolla un par motor (Tm), que tras ser transmitido por los órganos del sistema de transmisión, llega transformado hasta las ruedas motrices (Tr).
Como consecuencia de este par motriz en las ruedas, se origina una fuerza de tiro (F), según se vio en el apartado anterior, que es transmitida tangencialmente por el neumático de la rueda motriz del tractor al suelo.
Pues bien, si esta fuerza de tiro tangencial (F) en el punto de contacto del neumático con el suelo fuera mayor que la fuerza de adherencia (Fa) que soporta el suelo, entonces la rueda no rodaría sino que deslizaría, dado que el suelo se deformaría en exceso y el tractor patinaría sobre el terreno.
Por el contrario, si la fuerza motriz (F) que transmite la rueda es menor que la fuerza de adherencia (Fa) entonces la rueda motriz rodará sobre el suelo, sin deslizar, haciendo que el tractor avance correctamente en su marcha.
Por lo tanto:
• Si F > Fa → deslizamiento (No deseado)
• Si F < Fa → condición de rodadura
No obstante, y aunque la fuerza de tiro que desarrolle la rueda no supere la fuerza de adherencia, siempre se producirá un cierto deslizamiento entre la rueda y el suelo, por propia deformación de la rueda o del propio suelo, de manera que la mayor eficiencia a la tracción se obtiene limitando este deslizamiento. Como valores de referencia se acepta, en función del tipo de suelo y para tractores de simple tracción, o con la tracción delantera desconectada, los siguientes valores de pérdida por deslizamiento:
- Suelo pavimentado: 4 - 8 %
- Suelo firme: 8 - 10 %.
- Suelo labrado: 11 - 13 %.
- Suelo blando y arena: 14 - 16 %
De lo anterior se deduce que, el aumento de la fuerza de tiro (F) en la rueda motriz, para un mismo peso del tractor, hace aumentar el riesgo de patinamiento de la rueda, dado que se puede alcanzar a superar el valor de la fuerza adherente (F > Fa).
Para mitigar este riesgo, habría que aumentar el valor del límite de la fuerza de adherencia (Fa) que soporta el suelo en el punto de contacto con la rueda. Este valor, como se ha visto, depende del peso adherente que gravita sobre la rueda motriz, a partir de la expresión:
Fa = µa · QT
siendo,
QT es el peso total que gravita sobre la rueda motriz del tractor
µa es el coeficiente de adherencia.
- EJEMPLO DE CÁLCULO:
Siguiendo con los cálculos del ejemplo del apartado anterior, un tractor de 90 CV trabajando en una marcha corta con una relación de transmisión de 200:1, era capaz de desarrollar una fuerza de tiro de valor:
F = 59.322 N (6.047 kgf)
Trabajando el tractor sobre un terreno agrícola compuesto de rastrojo seco (coeficiente de adherencia, µa = 0,6), para que pudiera desarrollar toda esa fuerza de tiro, la adherencia deberá ser, al menos, igual también a ese valor (Fa = 6.047 kgf).
Por lo tanto, para que Fa = 6.047 kgf, tratándose de un tractor de simple tracción, sobre el eje motriz deberá gravitar al menos el siguiente peso:
QT = Fa / µa = 6047 / 0,6 = 10.078 kgf
Lo que significa tener que disponer sobre el eje motriz del tractor de un peso (considerando la masa del tractor, el peso del lastre que se coloca en los tractores, más el peso del apero) de más de 10 toneladas.
Esta masa no es habitual en tractores de 90 CV, por lo que se deduce que un tractor de estas características trabajando en marchas cortas nunca será capaz de desarrollar toda la fuerza de tiro que dispone, por carecer de peso suficiente que gravite sobre el eje motriz.
Por eso, en labores pesadas donde el tractor trabaje en marchas cortas, para aumentar la fuerza de tiro disponible se le añade lastre al tractor para así aumentar su peso. No obstante, esto perjudicará mucho las pérdidas por rodadura, como se verá más adelante, por lo que sólo deberá colocarse lastre adicional al tractor en momentos puntuales, trabajando con relaciones de marchas cortas y a bajas velocidades.
Como conclusión se puede decir que sólo entre el 50-60 % del peso del tractor se puede transformar en fuerza de tiro, por lo que un tractor de un peso de unos 3.000 kg sólo podrá tirar con una fuerza de unos 1.800 kgf, cualquiera que sea la potencia del motor del tractor.
3.5- Resistencia a la rodadura
Resulta intuitivo comprender que la fuerza de tiro necesaria para mover un remolque, por ejemplo, será mucho más elevada si el remolque está sobre un suelo arenoso o suelto que cuando se apoya sobre un pavimento firme y más duro como el asfalto. Para explicar este hecho surge el concepto de resistencia a la rodadura.

La resistencia a la rodadura es una fuerza que se opone al movimiento del tractor, y por tanto constituye una pérdida de rendimiento en el funcionamiento del tractor.
El valor que alcance la resistencia a la rodadura está en función del grado de hundimiento que experimentan las ruedas en el suelo y de la deformación de los neumáticos.
El valor de esta resistencia a la rodadura (Fr) se obtiene multiplicando el peso que gravita sobre las ruedas del tractor (QT) por el valor de un coeficiente, denominado coeficiente de rodadura (µr), característico del tipo de suelo por el que circula el tractor.
Fr = µr · QT
siendo,
Fr la fuerza de resistencia a la rodadura
QT es el peso total que gravita sobre la rueda motriz del tractor
µr es el coeficiente de rodadura.
En la siguiente tabla se muestran algunos valores característicos de este coeficiente de resistencia a la rodadura:
Tabla 2. Valores para el coeficiente de rodadura (µr) |
|
Naturaleza y tipo de suelo |
Coeficiente de rodadura (µr) |
Arena y suelo muy suelto |
0,15 a 0,30 |
Tierra labrada |
0,10 a 0,20 |
Rastrojo seco |
0,08 a 0,10 |
Suelo baldío |
0,06 a 0,10 |
Camino de tierra |
0,04 a 0,06 |
Camino de tierra afirmado |
0,03 a 0,05 |
Carretera asfaltada |
0,02 a 0,03 |
Carretera de cemento |
0,01 a 0,02 |
- |
0,0 a 0, |
- |
0,0 a 0,0 |
Como se ha visto en la expresión anterior, la resistencia a la rodadura es directamente proporcional al peso que gravita sobre las ruedas, por lo tanto, cuanto menor sea el peso del tractor, menor será la pérdida por rodadura.
Por tanto, para labores que se exija poco esfuerzo de tracción, se recomienda quitar el lastre de manera que se aligere el peso del tractor. Con ello, disminuiremos las pérdidas por rodadura, por lo que mejorará el rendimiento del tractor, que se traduce en un menor consumo de combustible.
Evidentemente, en labores pesadas que requieran de un gran esfuerzo de tiro, la disminución del peso del tractor aumentará los riesgos de patinamiento, como se ha visto en el apartado anterior. Por lo tanto, se tendrá que estudiar en cada caso el lastre necesario que habrá que incorporar en el tractor para optimizar el rendimiento, de manera que el peso total que gravite sobre las ruedas motrices sea el correcto para cada tarea.
ANEXOS Y TABLAS
Anexo 1- Caso práctico de cálculo de la capacidad de tracción de un tractor agrícola de 70 CV
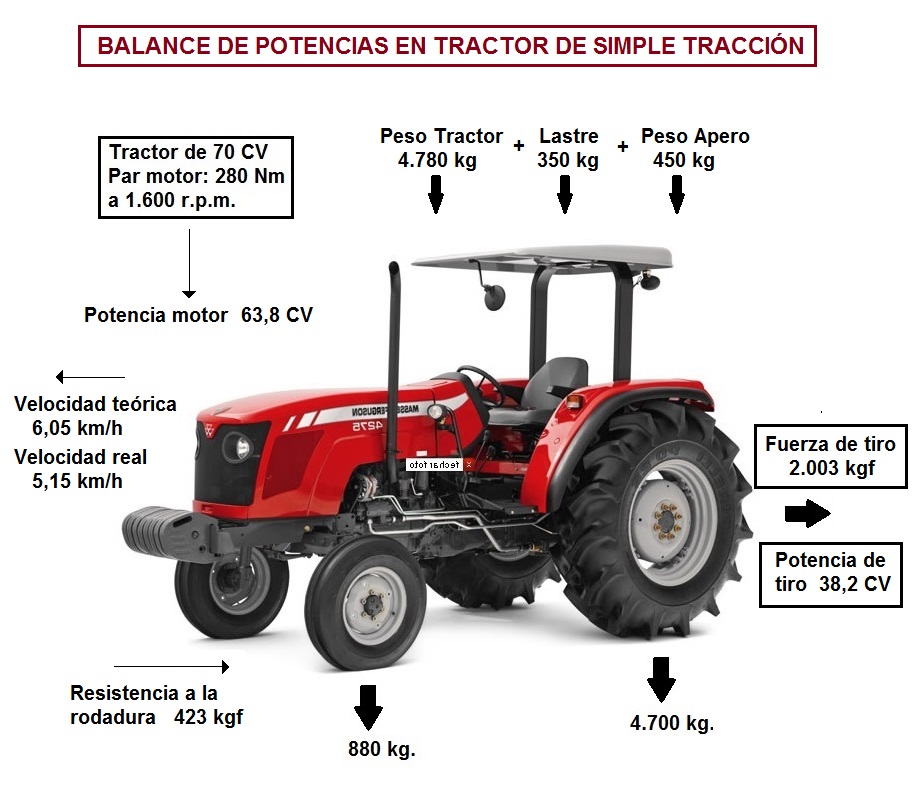
A continuación se va a llevar a cabo un caso práctico de análisis de la capacidad de tiro de un tractor agrícola de simple tracción de 70 CV de potencia de motor.
Se trataría de estudiar las prestaciones de este tipo de tractor de 70 CV en cuyas especificaciones técnicas, recogidas en el catálogo del fabricante, se indica que es capaz de desarrollar un par motor (Tm) de 280 N·m a un régimen de giro de 1600 r.p.m.
Para este caso práctico se va a suponer que el tractor realiza labores de arado en un terreno agrícola de rastrojo seco, empleando una marcha con una relación de transmisión de 80:1 (es decir, 1 vuelta de la rueda motriz por cada 80 vueltas del volante del motor).
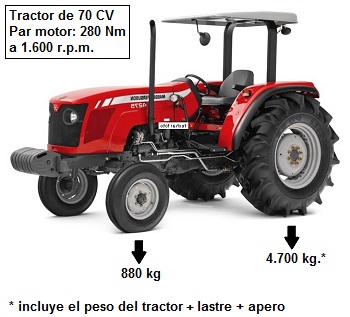
El peso total del tractor es de 4.780 kg, de los cuales 880 kg (18%) gravitan sobre el eje direccional delantero y 3.900 kg (82%) gravitan sobre el eje trasero motriz del tractor.
Además, del peso propio del tractor habrá que considerar otros pesos adicionales, como son:
- Peso del lastre instalado: 350 kg
- Parte del peso del arado que recae sobre el eje trasero del tractor: 450 kg.
Por tanto, el peso total que gravita sobre el eje trasero del tractor será de:
QT = 3900 + 350 + 450 = 4.700 kg
• Pérdidas por rodadura:
En primer lugar se van a calcular las pérdidas por rodadura de las ruedas sobre el suelo y que supone una pérdida de rendimiento en el funcionamiento del tractor.
Recordemos que esta resistencia a la rodadura es una fuerza que se opone al movimiento del tractor, y que debe vencerse para conseguir que el tractor avance.
Según el apartado 3.5 anterior, la expresión que permite calcular el valor de la resistencia a la rodadura (Fr) es:
Fr = µr · QT
siendo,
QT es el peso total que gravita sobre la rueda motriz del tractor
µr es el coeficiente de rodadura.
Para este caso práctico se tiene los siguientes valores:
QT = 4.700 kg es el peso total sobre el eje trasero del tractor
µr = 0,09 es el valor del coeficiente de rodadura para rastrojo seco (ver Tabla 2 del apartado anterior).
Sustituyendo en la expresión se tiene:
Fr = µr · QT = 0,09 · 4700 = 423 Kgf
Por tanto, las pérdidas que se originan por rodadura debida al desplazamiento del tractor es de 423 kgf.
• Velocidad real de avance:
Para calcular la velocidad de avance del tractor en su labor, se parte del régimen de giro de revoluciones del motor y de la relación de transmisión de la marcha de velocidades seleccionada. Para este caso práctico se tiene que:
- Revoluciones de giro del motor, nm = 1600 r.p.m.
- Relación de transmisión total, r = 80:1
En este ejemplo de cálculo se ha supuesto que el tractor trabaja empleando una marcha con una relación de transmisión final de 80:1, por lo que el régimen de giro de la rueda motriz del tractor es de:
Giro de la rueda motriz, nr = nm / r = 1600 / 80 = 20 r.p.m.
En el apartado 2.2 anterior se vio la expresión que permitía calcular la velocidad de avance del vehículo (V) en función del diámetro de la rueda motriz (D) y del régimen de giro del palier (nr) que engrana con la rueda:
|
π · D · nr |
|
V = |
|
|
|
60 |
|
donde,
V es la velocidad de marcha del vehículo, en m/s
D es el diámetro exterior de la rueda motriz, en m
nr es la velocidad de giro del palier o rueda, en revoluciones por minuto (r.p.m.)
Suponiendo que la rueda motriz del tractor de este ejemplo tiene un diámetro exterior D = 1600 mm., la velocidad lineal sería de:
|
π · 1,6 · 20 |
|
V = |
|
|
|
60 |
|
Que operando, resulta finalmente un velocidad de avance del tractor de:
V = 1,68 m/s (6,05 km/h)
Esta sería la velocidad teórica, pero habría que aplicar unas pérdidas por deslizamiento (ΔVdeslizamiento) de la rueda sobre el suelo que siempre se producen (ver apartado 3.4). Para el caso de un suelo agrícola tipo como el de este ejemplo, se puede considerar unas pérdidas del 15% por este concepto:
ΔVdeslizamiento = V · 15/100 = 0,25 m/s
Lugo, finalmente la velocidad real de avance del tractor será de:
Vreal = 1,68 - 0,25 = 1,43 m/s (5,15 km/h)
Luego, durante la labor de arado, el tractor avanzará a una velocidad de 5,15 km/h.
• Fuerza de tiro:
El cálculo de la fuerza de tiro (F) que realiza el tractor a través de las ruedas motrices se calcula, como se ha indicado en los apartados anteriores, a partir del par (Tr) de tiro que llega a las ruedas motrices:
|
Tr |
|
F = |
|
|
|
D / 2 |
|
donde,
Tr es el par transmisible por las ruedas motrices del tractor
D es el diámetro exterior de la rueda motriz.
Por otro lado, al par de tiro que llega finalmente a las ruedas motrices se puede obtener a partir del par motor (Tm) que desarrolla el motor del tractor y la relación final de transmisión (r) con la que trabaja:
Tr = Tm · r = 280 Nm · 80 = 22.400 N·m
Sin embargo, falta por considerar las pérdidas por rozamiento y otras causas originadas en el sistema de transmisión, desde el motor a los palieres de las ruedas, que hace disminuir el par de tiro real que llega finalmente a las ruedas motrices.
En el apartado 2.3 se indicó que resulta una buena aproximación considerar un rendimiento medio para una transmisión tipo del 85% (ηt = 0,85), por lo que finalmente, el par de tiro en las ruedas motrices del tractor es de:
Tr , real = Tr · ηt = 22.400 · 0,85 = 19.040 N·m
Suponiendo que la rueda motriz del tractor tiene un diámetro D = 1600 mm., la fuerza de tiro que puede desarrollar el tractor se calculará como:
|
19.040 |
|
F = |
|
|
|
0,8 |
|
Resultando una fuerza de tiro en barra de F = 23.800 N = 2.426 kgf.
Por último, habrá que considerar las pérdidas por rodadura. Las pérdidas por rodadura originadas en el desplazamiento del tractor también fueron calculadas, resultando ser:
Fr = 423 Kgf.
Por tanto, la fuerza de tiro real (FT) obtenida que puede desarrollar el tractor será de:
FT = F - Fr = 2426 - 423 = 2.003 Kgf = 19.649 N
Llegado a este punto, es necesario comprobar si el tractor puede desarrollar toda esta fuerza de tiro, o si por el contrario, por falta de adherencia en las ruedas motrices se produce el patinamiento de éstas, y el tractor no es capaz de desarrollar completamente toda la capacidad de tiro que puede ofrecer el motor.
En el apartado 3.4 se indicó que la condición necesaria para que el tractor fuera capaz de desarrollar toda la fuerza de tiro (F) y no se produjera el patinamiento de la rueda motriz, era que se cumpliera que:
F < Fa → condición de rodadura
donde Fa es la fuerza de adherencia presente en las ruedas motrices.
Por tanto, para que no haya patinamiento y el tractor pueda desarrollar toda la fuerza de tiro en la barra, es necesario que la fuerza de adherencia (Fa) sea igual, como mínimo, a la fuerza de tiro:
Fa = 2.426 kgf
Del apartado 3.4, la fuerza de adherencia (Fa) se calcula a partir de la siguiente relación:
Fa = µa · QT
siendo,
QT el peso total que gravita sobre la rueda motriz del tractor
µa es el coeficiente de adherencia.
En este caso práctico, se supone que el tractor se encuentra realizando una labor de arado sobre rastrojo seco. Para este tipo de terreno, según la tabla 1, se obtiene un coeficiente de adherencia µa = 0,60.
Despejando se puede obtener el peso necesario que debe gravitar sobre el eje motriz trasero del tractor, denominado peso adherente, para que pueda desarrollar toda la fuerza de tiro:
Pesoadherente = Fa / µa = 2426 / 0,6 = 4.043 kgf
Suponiendo que se produce un cierto deslizamiento entre la rueda y el suelo, por la propia deformación de la rueda o del suelo (se puede considerar un 12% para un suelo agrícola tipo), se obtiene finalmente el peso adherente que deberá gravitar sobre la rueda motriz del tractor:
Pesoadherente = 4.043 · 1,12 = 4.528 kgf
Al principio del ejercicio se indicó que el peso total que gravita sobre el eje trasero, considerando el peso propio del tractor, lastre y peso del apero, era de 4.700 kg. que es mayor que el peso adherente obtenido. Por lo tanto, en este caso el tractor sí podrá desarrollar toda la fuerza de tiro que ofrece el motor.
• Potencia de tiro disponible en barra:
En el apartado 3.1 se vio que la potencia de tiro (PT) que puede desarrollar en barra el tractor, depende de la fuerza de tiro real (FT) y de la velocidad de avance (V) del tractor, a partir de la expresión:
PT = FT · V
El valor de la fuerza de tiro en barra ya ha sido calculada anteriormente, resultando ser:
F = 2.426 kgf.
Por otro lado, las pérdidas por rodadura originadas en el desplazamiento del tractor también fueron calculadas, resultando ser:
Fr = 423 Kgf.
Por tanto, la fuerza de tiro real (FT) obtenida que puede desarrollar el tractor será de:
FT = F - Fr = 2426 - 423 = 2.003 Kgf = 19.649 N
La velocidad real de avance del tractor (V) también fue calculada, resultando ser:
Vreal = 1,43 m/s
Por tanto, la potencia de tiro (PT) máxima que el tractor podrá desarrollar en barra será de:
PT = FT · V = 19649 · 1,43 = 28.098 W = 28,1 kW = 38,2 CV.
Si se compara con la potencia que desarrolla el motor (Pm) en ese momento, se tiene que:
Pm = Tm · ωm
siendo Tm el par motor y ωm la velocidad angular de giro (rad/s) del eje del motor.
Para este caso práctico, el motor del tractor trabaja en las condiciones siguientes:
Par motor, Tm = 280 N·m
Revoluciones de giro del motor, ωm = 1600 r.p.m. = 167,5 rad/s
Por tanto, en este régimen de funcionamiento, la potencia (Pm) máxima que desarrolla el motor del tractor será de:
Pm = Tm · ωm = 280 · 167,5 = 46.900 W (63,8 CV)
Como se aprecia, de la potencia total que ofrece el motor (63,8 CV) sólo se podrá utilizar como potencia efectiva de tiro en barra 38,2 CV, lo que supone una eficiencia en la tracción de:
Eficiencia en la tracción = Potencia efectiva de tiro / Potencia motor = 38,2 / 63,8 = 0,60
En conclusión, como máximo sólo el 60% de la potencia total desarrollada por el motor del tractor se puede emplear en potencia de tiro efectiva, una vez que se han descontado las pérdidas originadas en la transmisión o las pérdidas por rodadura.
En realidad es inferior a este porcentaje, dado que por lo general el tractor suele trabajar a un régimen de potencia inferior a su valor máximo, con objeto de no forzar excesivamente su maquinaria. Por lo tanto, la potencia de tiro que realmente se suele obtener en barra apenas llega al 50% de la potencia máxima del motor, por lo que la eficiencia real de funcionamiento en los tractores agrícolas suele ser bajo.
Anexo 2- Fórmulas empíricas usadas en el cálculo de las prestaciones de los tractores agrícolas



>> FIN DEL TUTORIAL
Volver a
Tutoriales
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055

