- Tutorial nº 63 -
La Potencia y el Par Motor,
Estudio de la Cadena Cinemática,
Estabilidad en los Vehículos.
Índice de contenidos:
1- Par motor
1.1- Generalidades
1.2- Curva de par
2- Potencia
2.1- Generalidades
2.2- Curva de potencia
3- Consumo
3.1- Generalidades
3.2- Curva de consumo específico
4- Cadena cinemática
4.1- Generalidades
4.2- Velocidad del vehículo
4.3- Par transmisible por las ruedas motrices
5- Estabilidad
5.1- Deslizamiento y rodadura
5.2- Resistencia al movimiento de un vehículo
5.3- Pendiente superable
DESARROLLO DEL CONTENIDO
1- Par motor
1.1- Generalidades
En un motor de explosión de un vehículo, la combustión de la mezcla combustible-aire genera un aumento de la presión y temperatura en el interior de los cilindros del motor. Esta presión interior produce a su vez una fuerza (F) de empuje sobre el pistón que lo desplaza generando el clásico mecanismo de biela-manivela de los motores de combustión interna alternativos, donde el movimiento de traslación del pistón en el interior del bloque motor se transforma en un movimiento circular de giro del cigüeñal.
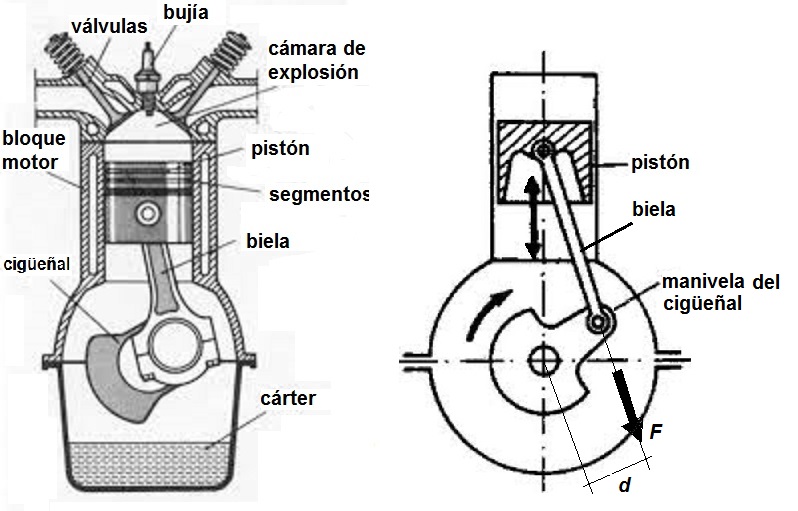
Figura 1. Mecanismo biela-manivela del motor de explosión
Pues bien, el par motor o "torque" (T) es el producto de la fuerza aplicada (F) de empuje a los cilindros por la distancia (d) al eje geométrico de giro del árbol del cigüeñal.
T = F · d
El par o torque motor se mide, según el Sistema Internacional de Unidades, en Newton metro (N·m), aunque también puede aparecer expresado a la inversa, metro Newton (m·N).
1.2- Curva de par
Intuitivamente se entiende que la fuerza (F) que produce el par motor es una fuerza variable, que en el caso de un motor de 4T es máximo en el momento que se produce la combustión de la mezcla y su posterior expansión en el cilindro, siendo negativa, esto es, no genera par motor en las demás fases (expulsión de gases, aspiración o llenado y compresión de la mezcla).
Y dentro de la fase donde se genera par motor (es decir, en la fase de combustión), el rendimiento del motor no es el mismo dependiendo del régimen de giro, y por ende el valor de la fuerza (F) de empuje que se genera.
Así, a bajas revoluciones la combustión de la mezcla no resulta óptima debido a la escasa inercia que poseen los gases, que provoca que el llenado del cilindro no sea el óptimo, al igual que su vaciado.
Y por otro lado, si el motor funciona a un elevado régimen, tampoco el llenado de los cilindros es completo, y ello es debido al escaso tiempo que dispone el gas para ocupar todo el recinto.
En consecuencia, la curva de par (T), que debería ser una recta horizontal, se convierte en una curva, con un tramo central casi recto que proporciona el máximo par, y las zonas extremas donde el par motor decrece según lo comentado anteriormente.
A continuación, se adjunta una gráfica con la curva par motor-potencia frente a las revoluciones de giro del motor, que puede responder a un caso general de vehículo:
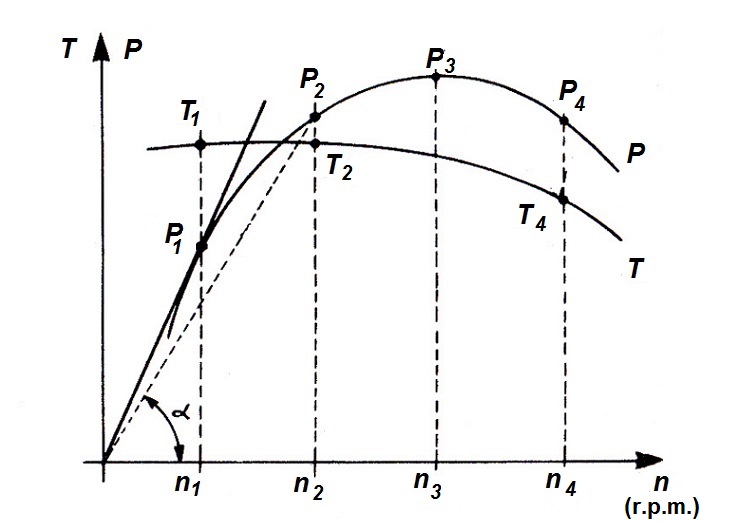
Figura 2. Curva de par motor y potencia
Efectivamente, en la gráfica anterior se puede comprobar cómo es, de forma genérica, la curva de par motor (T), además de la de potencia, pero ésta se estudiará más adelante. En ella se representa en el eje horizontal las revoluciones por minuto (r.p.m.) de régimen giro (n) del motor y en el eje vertical el par (T) que proporciona durante todo su rango de funcionamiento.
En los motores de combustión, la curva de par empieza siendo ascendente hasta llegar a las revoluciones donde el motor rinde el par máximo (T1), que es el punto de diseño óptimo. A partir de ese momento, el par comienza a disminuir progresivamente.
Esto es así, porque a partir del punto óptimo de revoluciones del motor empiezan a aparecer dificultades, como ya se han comentado anteriormente algunas, y que están relacionadas fundamentalmente con los siguientes factores:
- Una inadecuada evacuación de gases quemados conforme aumenta las revoluciones del motor, según se ha visto;
- Insuficiente llenado de aire en cada ciclo;
- La combustión empieza a no ser óptima;
- La fracción de tiempo para cada combustión se reduce;
- La mezcla de aire-combustible no se acaba de completar;
- El avance a la inyección no es suficiente.
En consecuencia, aunque quememos más combustible acelerando el motor y consiguiendo que la potencia todavía aumente, el par desciende. De ahí que los consumos específicos óptimos estén en valores próximos a la zona de par máximo, aumentando el consumo del motor conforme se aleja de este rango.
Una curva con una gran zona plana en el centro (como la que presentan la gran mayoría de motores diesel), define un motor muy elástico, es decir, con poca necesidad de cambiar de marchas para adaptarse a los cambios de conducción. Ello es así, porque un motor elástico, que dispone del par elevado en un amplio rango de revoluciones, permite acelerar con fuerza, incluso en marchas largas, sin tener que hacer uso del cambio de marchas. Gracias e ello, con un motor más elástico es posible circular empleando marchas más largas, revolucionando menos el motor y por tanto, mejorando el consumo.
En efecto, en el caso de los motores diesel la curva de par es prácticamente horizontal para un amplio rango de revoluciones del motor, incluso en niveles próximos al ralentí del motor. Esto garantiza un buen par motor incluso a bajas revoluciones, lo cual resulta muy útil en situaciones difíciles, como pueda ser reanudar la marcha con el vehículo parado en una pendiente.
2- Potencia
2.1- Generalidades
La potencia (P) desarrollada por el par motor (T) viene dada por la siguiente expresión:
P = T · ω
Siendo (ω) la velocidad angular de giro (rad/s) del eje de transmisión o eje del cigüeñal.
La potencia del motor se mide, según el Sistema Internacional de Unidades, en watios (W).
En ocasiones es interesante conocer la potencia en función de las revoluciones por minutos (r.p.m.) a la que gira el motor en vez de la velocidad angular. En efecto, si (n) son las revoluciones por minuto a la que gira el motor, entonces la potencia (P) se expresa como sigue,
|
T · n |
|
P = T · ω = |
|
|
|
60 / 2·π |
|
que aproximadamente resulta,
|
T · n |
|
P = |
|
|
|
9,55 |
|
donde,
P, es la potencia motor, en W;
T, es el par motor, en N·m;
n, son las revoluciones por minuto de giro del motor (r.p.m.)
Pero también resulta útil conocer la potencia expresada en otras unidades de uso muy común, como son: HP y CV.
- HP (Horse Power): o caballo de potencia, es la unidad de medida de la potencia empleada en el sistema anglosajón de unidades, y se define como la potencia necesaria para levantar a la velocidad de 1 pie/minuto un peso de 32572 libras.
Sus equivalencias con otros sistemas son las siguientes:
• 1 HP = 745,69987 W
• 1 HP = 1,0139 CV
Por lo que la anterior expresión de la potencia (P) en función del par y las revoluciones del motor podría expresarse de la siguiente manera:
|
T · n |
|
PHP = |
|
|
|
7120,91 |
|
donde,
PHP, es la potencia motor, expresada en HP;
T, es el par motor, en N·m;
n, son las revoluciones por minuto de giro del motor (r.p.m.)
- CV (Caballo de Vapor): Unidad de medida que emplea unidades del sistema internacional, y se define como la potencia necesaria para levantar un peso de 75 Kgf. en un segundo, a un metro de altura.
Y sus equivalencias con otros sistemas son las siguientes:
• 1 CV = 735,49875 W
• 1 CV = 0,9863 HP
Y la potencia (P) en función del par y las revoluciones del motor quedaría de la siguiente manera:
|
T · n |
|
PCV = |
|
|
|
7023,50 |
|
donde,
PCV, es la potencia motor, expresada en CV;
T, es el par motor, en N·m;
n, son las revoluciones por minuto de giro del motor (r.p.m.)
Por último, y en el caso que el par motor (T) estuviera expresado en kgf·m, entonces la expresión anterior que proporciona la potencia del motor (P) se expresaría como:
|
T · n |
|
PCV = |
|
|
|
716,2 |
|
donde,
PCV, es la potencia motor, expresada en CV;
T, es el par motor, pero esta vez expresado en kgf·m;
n, son las revoluciones por minuto de giro del motor (r.p.m.)
Por otro lado, la fuerza motriz (F) transmitida por el neumático al suelo, en función de la potencia del motor (P) y la velocidad de marcha del vehículo (V), se puede expresar como:
|
75 · ηt · P |
|
F = |
|
|
|
V |
|
donde,
P es la potencia motor, en CV;
V es la velocidad de marcha del vehículo, en m/s;
ηt es el rendimiento total de la cadena cinemática de transmisión, expresado en tanto por uno;
F es la fuerza motriz transmitida por el neumático al suelo, en kgf.
El rendimiento total de la cadena de transmisión (ηt) se obtendrá a partir de los rendimientos de cada uno de los elementos y órganos que constituyen el sistema de transmisión, desde el eje de salida del motor hasta el palier de la rueda (embrague, caja de cambios, ejes de transmisión, grupo cónico-diferencial o mecanismo reductor del eje motriz), es decir:
ηt = η1 · η2 · ... · ηn
En la mayoría de los vehículos que dispongan de un sistema de transmisión clásica, este rendimiento total (ηt) de la cadena de transmisión estará comprendido entre un 80 y un 90%.
2.2- Curva de potencia
En la siguiente gráfica se representa de nuevo la curva conjunta de potencia (P) y par motor (T), en función de la velocidad de giro (n) en r.p.m. para un motor tipo.

Figura 3. Curva de potencia y par motor
Como se puede observar de la anterior figura, la potencia que puede ofrecer un motor de combustión interna tipo aumenta conforme sube de régimen de giro, hasta un máximo (representado por P3) que se alcanza cuando gira a n3 (r.p.m.).
En estas condiciones, aunque se acelere más la velocidad del motor, éste no es capaz de entregar más potencia dado que la curva entra en su tramo descendente. El límite máximo de revoluciones a la que puede girar el motor lo marca n4, establecido por las propias limitaciones de los elementos mecánicos que lo constituyen.
Lo primero que se puede comprobar es que la máxima potencia no corresponde con el régimen del máximo par motor (punto de revoluciones n1). En la mayoría de los casos, el punto de par máximo se encuentra en torno al 70% del régimen nominal, es decir, de aquel al que se produce la máxima potencia.
Esto es así porque según se vio en al apartado 2.1 anterior, la potencia es el producto del par motor por el número de vueltas, y aunque se alcance el punto donde se comienza ligeramente a disminuir el par que ofrece el motor, este efecto se compensa por el aumento, que proporcionalmente es mayor, del régimen de giro del motor, y por ello su producto, que proporciona la potencia, sigue aumentando.
En otro orden de cosas, el rango de velocidades que produce un funcionamiento estable del motor, según la gráfica de la figura 3 anterior, sería el comprendido entre el régimen de velocidades n1 y n2, valores que por otro lado no se corresponde con el punto de máxima potencia.
En efecto, si el motor se encuentra funcionando a un régimen de velocidades entre n1 y n2, cualquier situación cambiante que se produzca durante la conducción y que suponga un aumento del par resistente, por ejemplo al subir una carretera en pendiente, el motor se adapta automáticamente disminuyendo su régimen de giro porque esto supone que aumentará el par motor. Y análogamente, si de nuevo baja el momento resistente, por ejemplo al volver a un tramo sin pendiente en la carretera, las necesidades del par motor son menores que se consigue automáticamente aumentando la velocidad del motor.
En los motores diesel la curva de par es prácticamente horizontal para un amplio rango de revoluciones del motor, como ya se vio en el apartado anterior, mientras que la curva de potencia se aproxima a una recta que pasa por el origen, como se comprueba en la figura 4 adjunta.
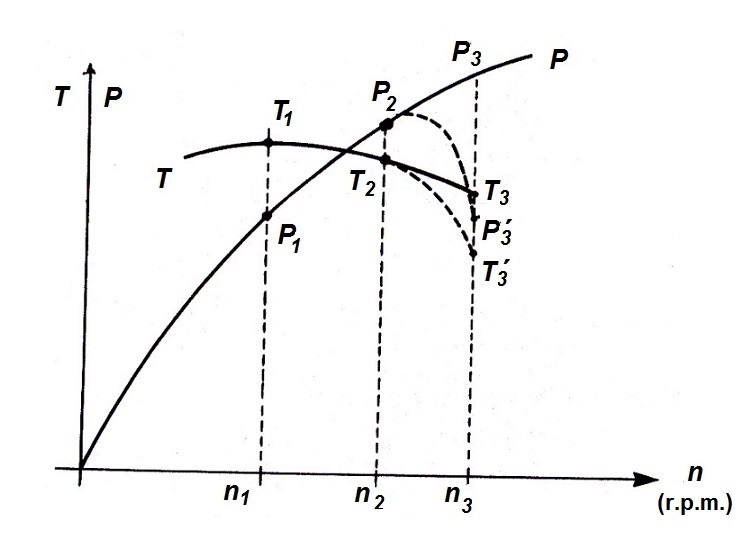
Figura 4. Curva de par y potencia en un motor diesel
El disponer en los motores diesel de una curva de potencia tan pronunciada y ascendente, indica que en este tipo de motores a más revoluciones se obtiene mayor potencia. Este hecho unido a que el par permanece prácticamente constante, cualquier disminución en el par resistente con la que se encuentre el vehículo, por ejemplo, en una carretera llana o ligeramente descendente, ocasionaría un aumento brusco de las revoluciones del motor.
Por ello, y para evitar que el motor se embale se incluye en los motores diesel un elemento regulador que a partir de cierta velocidad de giro reduce la cantidad de combustible inyectado, reduciendo de este modo el par y la potencia que ofrece el motor (situación indicada con los puntos P´3 y T´3, de la figura 4). De este modo a la máxima velocidad de funcionamiento sólo podrá funcionar el motor en vacío, evitando así que el motor se revolucione de manera descontrolada.
3- Consumo
3.1- Generalidades
El consumo, y en concreto el consumo específico (C), se define como el caudal de combustible que consume el motor o consumo horario por la potencia que proporciona. El consumo específico se mide en g/kWh.
El consumo específico proporciona información sobre el rendimiento del motor. Cuanto menor sea su consumo específico, mejor es su rendimiento.
El rendimiento de un motor indica la proporción de energía útil empleada en mover el vehículo de la total obtenida con la combustión en el motor. En los mejores motores diesel, este rendimiento apenas supera el 40%, mientras que en los motores de gasolina se queda por debajo de esa cifra.
Las causas de este rendimiento tan bajo en los vehículos actuales son debidas, entre otros factores, a que se emplea gran parte de la energía producida en el motor en aspectos como vencer la resistencia a la rodadura del vehículo sobre la carretera (rozamiento del neumático con el asfalto...), pérdidas en la cadena de transmisión (embrague, caja de cambios, cojinetes...), consumo de elementos auxiliares del vehículo (aire acondicionado, iluminación...), etc.
3.2- Curva de consumo específico
En general, la curva de consumo específico suele seguir un comportamiento inverso a la curva del par, es decir, en las condiciones de par máximo se consigue un consumo específico mínimo.
En la siguiente figura, se incluye la curva de consumo específico (C), junto con las demás curvas de potencia (P) y par motor (T), y donde se puede comprobar el comportamiento de cada variable según el régimen de funcionamiento del motor.
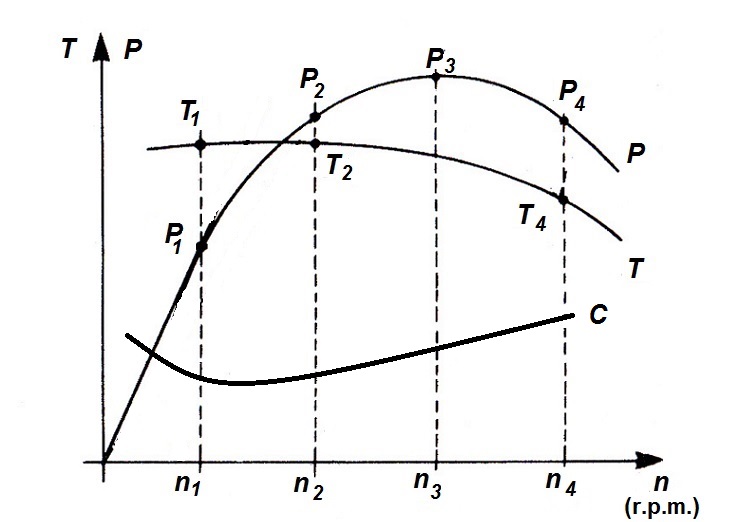
Figura 5. Curva de potencia-par-consumo específico
4- Cadena cinemática
4.1- Generalidades
La cadena cinemática de un vehículo automóvil la constituye el conjunto de órganos y mecanismos encargado de transmitir el movimiento desde su generación (en el motor) hasta las ruedas motrices.
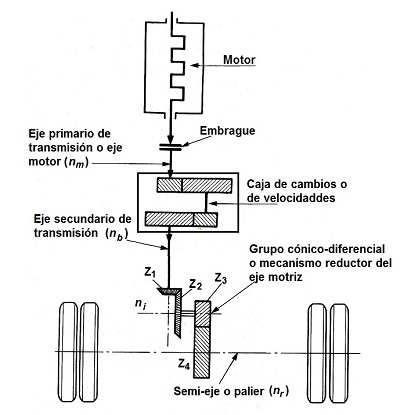
Dentro de los componentes que constituyen la cadena cinemática de un vehículo se pueden distinguir dos grandes grupos:
• el motor, que es el foco de generación del movimiento, y
• el sistema de transmisión, encargado de transmitir este movimiento desde su generación hasta su destino final en las ruedas motrices del vehículo.
A su vez, el sistema de transmisión de un vehículo está compuesto por los siguientes órganos de transmisión del movimiento:
• embrague;
• caja de cambios de marchas o de velocidades;
• ejes de transmisión, entre los cuales se distingue el eje primario que conecta la salida del embrague del motor con la entrada a la caja de velocidades, y el eje secundario de transmisión que conecta la salida de la caja de velocidades con la entrada al grupo cónico-diferencial instalado en el eje motriz;
• el grupo cónico-diferencial que es un mecanismo reductor instalado en el tren del eje motriz;
• los palieres o semiárboles que conectan el grupo diferencial con las ruedas motrices;
• las ruedas motrices.
4.2- Velocidad del vehículo
En este apartado se va a detallar cómo calcular la velocidad (V) de marcha de cualquier vehículo en función del número de revoluciones de giro del motor (nm) y del diámetro de las ruedas motrices (D), para unos valores determinados de relaciones de transmisión de la cadena cinemática.
En efecto, si D es el diámetro de la rueda motriz y nr es la velocidad de giro del palier que conecta con la rueda, y que por lo tanto es la misma que la de la rueda (ver la figura del apartado 4.1 anterior), entonces se tiene que:
|
π · D · nr |
|
V = |
|
|
|
60 |
|
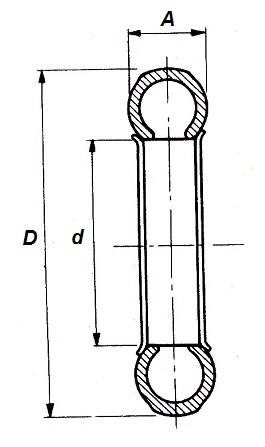
donde,
V es la velocidad de marcha del vehículo, en m/s;
D es el diámetro exterior de la rueda motriz, en m;
nr es la velocidad de giro del palier o rueda, en revoluciones por minuto (r.p.m.)
Como se ve en la figura adjunta, se denota con D al diámetro exterior del neumático, mientras que d es el diámetro de la llanta sobre la que se monta el neumático y A es la anchura del neumático.
Tanto el diámetro de la llanta (d) como el ancho del neumático (A) suelen venir grabados, y generalmente se expresan en pulgadas. Así, por ejemplo, un neumático que lleve inscrito 12,00x20, indica que el ancho del neumático es de 12" y que el diámetro de la llanta es 20".
Pero volviendo al estudio de la cadena cinemática del vehículo, si se llama rc a la relación de transmisión que se tenga en la caja de cambios de velocidades, se tendrá que:
|
nb |
|
rc = |
|
|
|
nm |
|
donde,
nb es la velocidad de giro del eje secundario a la salida de la caja de cambios, en r.p.m.
nm es la velocidad de giro del motor, en r.p.m.
NOTA: Se recomienda visualizar la figura del apartado 4.1 anterior para comprender mejor los términos descritos.
Del mismo modo, para el eje motriz se tiene que la relación de transmisión rd que se obtiene en el grupo cónico-diferencial instalado en el eje motriz, se expresa como:
|
nr |
|
rd = |
|
|
|
nb |
|
donde,
nr es la velocidad de giro del palier o rueda a la salida del grupo cónico-diferencial, en r.p.m.
nb es la velocidad de giro del eje secundario a la salida de la caja de cambios y que conecta a su vez con el grupo cónico-diferencial del eje motriz, en r.p.m.
Multiplicando miembro a miembro las dos anteriores expresiones se tiene que:
|
nr |
|
rc · rd = |
|
|
|
nm |
|
Y por lo tanto,
nr = nm · rc · rd
Sustituyendo el anterior valor de nr en la expresión que proporciona la velocidad de marcha del vehículo (V) del comienzo de este apartado se tiene que:
|
π · D · nr |
|
V (m/s) = |
|
|
|
60 |
|
O sea que,
|
π · D · nm · rc · rd |
|
V (m/s) = |
|
|
|
60 |
|
La anterior expresión proporciona el valor de la velocidad (V) en m/s (metros/segundo). Si se prefiere la velocidad en kilómetros/hora se tiene esta otra expresión:
|
3 · π · D · nm · rc · rd |
|
V (km/h) = |
|
|
|
50 |
|
Como se puede deducir de la anterior expresión, para valores fijos de rc y de rd, la velocidad del vehículo (V) dependerá del número de revoluciones del motor (nm) y del diámetro de la rueda motriz (D).
Y por otro lado, para valores fijos de nm, D y rd, la velocidad del vehículo (V) dependerá de la relación de la caja de cambios rc.
4.3- Par transmisible por las ruedas motrices
Del apartado 4.1 anterior, se sabe que el sistema de transmisión de un vehículo está compuesto por los siguientes órganos:
• embrague;
• caja de cambios;
• ejes de transmisión;
• el grupo cónico-diferencial;
• los palieres o semiárboles que conforman el eje motriz;
• las ruedas motrices.
Es evidente que en cada uno de los anteriores órganos que componen el sistema de transmisión de un vehículo se producen pérdidas debidas al rozamiento entre piezas y a otras causas, que hacen que la potencia final transmitida a las ruedas motrices sea menor que la potencia generada en el propio motor.
En este sentido se define el rendimiento de la transmisión (ηt) a la relación entre la potencia finalmente transmitida por las ruedas motrices (Pr) y la potencia que transmite el motor (Pm). Es decir:
|
Pr |
|
ηt = |
|
|
|
Pm |
|
El rendimiento total de la cadena de transmisión (ηt) se obtiene a partir de los rendimientos de cada uno de los elementos y órganos que lo constituyen, desde el eje de salida del motor hasta el palier de la rueda, es decir, embrague, caja de cambios, ejes de transmisión, grupo cónico-diferencial:
ηt = η1 · η2 · ... · ηn
En la mayoría de los vehículos que dispongan de un sistema de transmisión clásica, este rendimiento (ηt) de la cadena de transmisión estará comprendido entre un 80 y un 90% (entre un 80-85% en velocidades cortas, y entre un 85-90% para velocidades largas).
Considerar un rendimiento medio para una transmisión del 85% suele ser una buena aproximación para la mayoría de los casos.
Por otro lado, y recordando lo dicho en el apartado 2.1, se tenía que la expresión que permite calcular la potencia entregada por el motor era la siguiente:
|
Tm · nm |
|
Pm = |
|
|
|
716,2 |
|
donde,
Pm es la potencia motor, expresada en CV;
Tm es el par transmisible por el motor, en kgf·m;
nm son las revoluciones por minuto de giro del motor (r.p.m.)
Y por otro lado, la potencia transmisible por las ruedas motrices (Pr), vendrá igualmente dada por esta otra expresión:
|
Tr · nr |
|
Pr = |
|
|
|
716,2 |
|
donde,
Pr es la potencia transmisible por las ruedas motrices, expresada en CV;
Tr es el par transmisible por las ruedas motrices, en kgf·m;
nr son las revoluciones por minuto de giro de las ruedas motrices (r.p.m.)
Teniendo en cuenta que el rendimiento de la transmisión (ηt) se expresa como:
|
Pr |
|
ηt = |
|
|
|
Pm |
|
sustituyendo los valores de Pm y de Pr , se tiene que:
|
Tr · nr |
|
ηt = |
|
|
|
Tm · nm |
|
Es decir, que el par transmisible por las ruedas motrices (Tr) se puede expresar como:
|
ηt · Tm · nm |
|
Tr = |
|
|
|
nr |
|
Pero como se vio en el apartado 4.2 anterior, las revoluciones de giro de las ruedas motrices (nr) se podían expresar como:
nr = nm · rc · rd
Sustituyendo, resultará finalmente que el par transmisible (Tr) por las ruedas motrices de un vehículo se podrá expresar como:
|
ηt · Tm |
|
Tr = |
|
|
|
rc · rd |
|
donde,
ηt es el rendimiento total de la transmisión del vehículo;
Tm es el par motor;
rc es la relación de transmisión en la caja de cambios;
rd es la relación de transmisión en el grupo cónico-diferencial del eje motriz.
Por último, ya conocido el par que transmite las ruedas motrices (Tr), se podría obtener también el esfuerzo tangencial (F) que transmite las ruedas al suelo.
Este esfuerzo ya se vio una forma de calcularlo en el apartado 2.1 a partir de la potencia del motor y la velocidad de marcha del vehículo. Así que aquí se expondrá otra forma de calcularlo.
En efecto, por definición del par de fuerzas, se tiene que el esfuerzo tangencial (F) que realizan las ruedas motrices en el suelo en función del par que desarrollan, vale:
|
Tr |
|
F = |
|
|
|
D / 2 |
|
Donde D es el diámetro exterior de las ruedas motrices.
Sustituyendo entonces la expresión de la formulación anterior que permitía obtener el par de las ruedas motrices (Tr) en función del par motor (Tm), se tiene que:
|
2 · ηt · Tm |
|
F = |
|
|
|
D · rc · rd |
|
donde,
F es la fuerza motriz transmitida tangencialmente por el neumático al suelo;
ηt es el rendimiento total de la transmisión del vehículo;
Tm es el par motor;
rc es la relación de transmisión en la caja de cambios;
rd es la relación de transmisión en el grupo cónico-diferencial del eje motriz.
D es el diámetro de las ruedas motrices.
5- Estabilidad
5.1- Deslizamiento y rodadura
Como se sabe, cuando un cuerpo se encuentra apoyado en el suelo y queremos arrastrarlo o deslizarlo, la fuerza que se opone a este movimiento de deslizamiento por el suelo se denomina fuerza de rozamiento o adherencia, la cual se establece entre la superficie en contacto del cuerpo con el suelo.
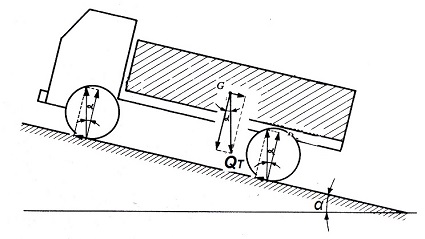
Pues bien, trasladado este concepto a los vehículos, si se supone un vehículo que se encuentra parado en una pendiente, con las ruedas bloqueadas, la fuerza que impide a que el vehículo se deslice pendiente abajo es precisamente la adherencia de los neumáticos al suelo.
La magnitud de esta fuerza de adherencia (Fa) entre el vehículo y el suelo viene dada por la siguiente expresión:
Fa = µa · QT · cosα
donde,
QT es el peso total del vehículo, aplicado en su c.d.g.
α es el ángulo que forma el plano inclinado de la carretera con la horizontal
µa es un coeficiente adimensional, llamado coeficiente de adherencia.
El coeficiente de adherencia (µa) es un valor que se obtiene experimentalmente, pues depende tanto de la naturaleza del terreno o pavimento sobre el que circule el vehículo, como del estado y naturaleza de los neumáticos.
En la siguiente tabla se muestran unos valores orientativos para el coeficiente de adherencia (µa), considerándose para todos los casos que el vehículo disponga de los neumáticos en buen estado:
Tabla 1. Valores para el coeficiente de adherencia (µa) |
|
Estado del pavimento |
Coeficiente de adherencia (µa) |
Carretera de cemento |
0,8 |
Empedrado seco |
0,7 |
Asfalto seco |
0,6 a 0,75 |
Carretera húmeda |
0,3 a 0,4 |
Carretera mojada |
0,25 |
Carretera alquitranada y grasienta |
0,15 a 0,20 |
Carretera con barro |
0,15 |
Carretera con hielo |
0,08 a 0,1 |
Para cálculos generales, se suele emplear como valor medio del coeficiente de adherencia, µa = 0,6.
- Rodadura:
Como ya se ha explicado anteriormente, el motor de un vehículo desarrolla un par motor, que tras ser transmitido por los órganos del sistema de transmisión, llega hasta las ruedas motrices.
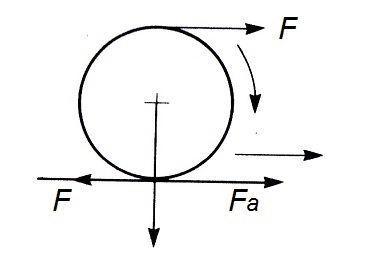
Como consecuencia de este par motriz, en las ruedas motrices se crea una fuerza tangencial (F), según se vio en el apartado anterior, que es transmitida tangencialmente por el neumático en el punto de contacto con el suelo.
Pues bien, si esta fuerza tangencial (F) que se genera en el punto de contacto del neumático con el suelo, fuera mayor que la de adherencia (Fa) entre las ruedas motrices y el suelo, entonces la rueda no rodaría sino que deslizaría y patinaría sobre el terreno.
Por el contrario, y como ocurre normalmente, si la fuerza motriz (F) que transmite la rueda es menor que la fuerza de adherencia (Fa) entonces la rueda motriz rodará, haciendo que el vehículo avance correctamente en su marcha.
Ello es así, porque en las ruedas motrices se creará un par llamado "par de rodadura", que se resiste al movimiento, y que hace que la rueda ruede y no deslice sobre el terreno.
Por lo tanto:
• Si F > Fa → deslizamiento (No deseado)
• Si F < Fa → condición de rodadura
Por otro lado, este par de rodadura que hace que la rueda no deslice, lleva aparejado, como todo par de fuerzas, un esfuerzo o fuerza, que se llama resistencia a la rodadura (Rr), cuyo valor se obtiene por la siguiente expresión:
Rr = µr · QT
donde,
QT es el peso total del vehículo, aplicado en su c.d.g.
µr es un coeficiente adimensional, llamado coeficiente de rodadura.
De igual manera, el coeficiente de rodadura (µr) es un coeficiente adimensional que se obtiene experimentalmente, dado que depende de múltiples factores como el estado y la presión de los neumáticos, de la naturaleza y estado del piso, de la velocidad del vehículo, etc.
En la siguiente tabla se indican valores comunes para el coeficiente de rodadura (µr) según el estado del pavimento y para unas condiciones normales de circulación y estado de conservación del vehículo:
Tabla 2. Valores para el coeficiente de rodadura (µr) |
|
Estado del pavimento |
Coeficiente de rodadura (µr) |
Carretera de cemento |
0,0125 |
Empedrado seco |
0,015 |
Carretera asfaltada |
0,02 a 0,03 |
Terreno natural duro |
0,08 |
Terreno de consistencia media |
0,11 |
Terreno arenoso |
0,15 a 0,30 |
Para cálculos generales, se suele emplear como valor medio del coeficiente de rodadura, µr = 0,02 - 0,03.
5.2- Resistencia al movimiento de un vehículo
Todo vehículo para poder desplazarse deberá vencer tres tipos de resistencias, a parte de otros fenómenos puntuales, como baches en la carretera, piedras sobre el camino, etc., que son:
- Resistencia a la rodadura (Rr);
- Resistencia por la pendiente de la carretera (Rp);
- Resistencia debida al aire o resistencia aerodinámica (Ra).
A continuación, se procederá a estudiar cada uno de los tipos anteriores de resistencia por separado:
- Resistencia a la rodadura (Rr):
Este tipo de resistencia ya se estudió en el apartado anterior. La expresión que permite calcular esta resistencia también se vio, y era la siguiente:
Rr (kgf) = µr · QT
donde,
QT es el peso total del vehículo, aplicado en su c.d.g., en kg.
µr es el coeficiente de rodadura, cuyo valor se puede obtener de la tabla 2 del apartado anterior.
Por otro lado, la potencia necesaria que el vehículo debe absorber para poder superar este tipo de resistencia, viene dada por la siguiente expresión:
|
Rr · V |
|
Pr (C.V.) = |
|
|
|
270 |
|
Pero como Rr = µr · QT , la anterior expresión quedaría como sigue:
|
µr · QT · V |
|
Pr (C.V.) = |
|
|
|
270 |
|
Donde V es la velocidad a la que circula el vehículo en km/h.
No obstante, el motor del vehículo deberá desarrollar una potencia mayor, debido a las pérdidas que se producen en los órganos de transmisión. Para ello se estableció el llamado rendimiento total de la cadena de transmisión (ηt), ya visto anteriormente, con el que se tiene en cuenta este tipo de pérdidas.
De esta manera, la potencia que deberá desarrollar el motor para superar la resistencia a la rodadura del vehículo se calculará como:
|
Pr |
|
Pr,m = |
|
|
|
ηt |
|
Siendo ηt el rendimiento total del sistema de transmisión del vehículo.
- Resistencia por la pendiente de la carretera (Rp):
Por definición exacta, se denomina pendiente de la carretera (i) a la tangente del ángulo inclinado que forma el piso de la carretera con la horizontal, es decir, i = tgα = h/L', según la figura que se adjunta a continuación.
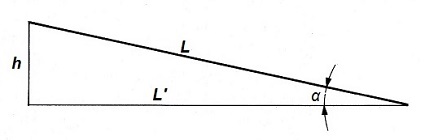
Pero para ángulos pequeños, como ocurre en la inmensa mayoría de las pendientes en los trazados de carretera, se puede simplificar diciendo que:
L' ≈ L ; tgα ≈ senα ; cosα = 1
Es común, expresar la pendiente de las carreteras en tanto por ciento, es decir, para valores de L = 100 m. En este caso, la expresión que definiría la pendiente de la carretera quedaría como sigue:
i = tgα ≈ senα = h/100
De este modo, si QT es el peso total del vehículo aplicado en su c.d.g., cuando éste sube por una carretera en pendiente, parte de su peso se opondrá a su movimiento ascendente.
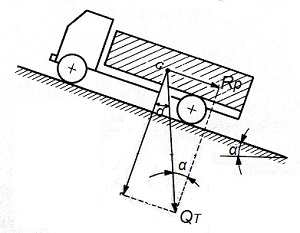
Precisamente, este valor resistente debido a la pendiente de la carretera (Rp), se expresará según la siguiente formulación:
Rp (kgf) = QT · senα = QT · i
De la misma manera, la potencia necesaria para vencer esta resistencia se expresa mediante la siguiente formulación:
Pp (C.V.) = Rp · V / 270
Pero como Rp = QT · senα = QT · i, la anterior expresión quedaría como sigue:
Pp (C.V.) = i · QT · V / 270
Donde V es la velocidad a la que circula el vehículo en km/h.
Del mismo modo, el motor del vehículo deberá desarrollar una potencia mayor que la anteriormente expresada, para tener en cuenta las pérdidas originadas en el sistema de transmisión.
Así pues, la potencia que deberá desarrollar el motor para superar la resistencia por la pendiente de la carretera se calculará mediante la expresión:
|
Pp |
|
Pp,m = |
|
|
|
ηt |
|
Siendo ηt el rendimiento total del sistema de transmisión del vehículo.
- Resistencia aerodinámica (Ra):
Este tipo de resistencia es la que ofrece la masa de aire de la atmósfera al movimiento del vehículo. La expresión que permite calcular este tipo de resistencia, expresada en kgf, es la siguiente:
Ra (kgf) = Ca · S · V(m/s)2
donde,
V(m/s) es la velocidad del vehículo, pero aquí expresada en m/s;
S es la superficie frontal efectiva que ofrece el vehículo, perpendicular al sentido de la marcha, en m2;
Ca es un coeficiente de penetración aerodinámica, y cuyos valores normales se exponen en la siguiente tabla:
Tabla 3. Valores del coeficiente aerodinámico (Ca) |
|
Tipo de vehículo |
Coeficiente aerodinámico (Ca) |
Camiones |
0,050 |
Vehículos articulados y trenes de carretera |
0,095 |
Autobuses y autocares |
0,038 |
Autobuses con perfil aerodinámico |
0,019 |
Turismos normales |
0,022 a 0,035 |
Turismos con perfil aerodinámico |
0,010 a 0,019 |
La superficie transversal efectiva del vehículo (S) que ofrece resistencia al aire, a efectos de cálculos, se obtiene tomando como base el ancho de vía del eje delantero (la distancia entre ruedas, d) por la altura máxima del vehículo (H).
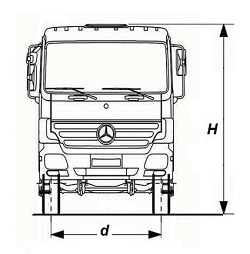
Evidentemente, la sección real del vehículo que va a ofrecer la resistencia al aire es inferior al valor anterior, por lo que se suele afectar de un coeficiente corrector (c) que acerque el valor del área efectiva (S) al valor de la sección real transversal del vehículo. De esta manera se tiene que:
S = c · d · H
De este modo, la resistencia al aire del vehículo, expresada en kgf, quedará de la siguiente manera:
Ra (kgf) = Ca · c · d · H · V(m/s)2
donde,
V(m/s) es la velocidad del vehículo, expresada en m/s;
H es la altura máxima del vehículo, en m;
d es la distancia transversal entre las ruedas delanteras, en m;
c es el coeficiente corrector del área transversal efectiva del vehículo, cuyo valor varía entre 0,85 y 0,95.
Ca es el coeficiente de penetración aerodinámica, cuyos valores normales se exponen en la tabla 3 anterior.
Por otro lado, indistintamente se suele emplear la velocidad del vehículo expresada en km/h, o bien, en m/s. La relación entre ambas formas de expresar la velocidad es la siguiente:
|
V |
|
V(m/s) = |
|
|
|
3,6 |
|
donde V es la velocidad expresada en km/h, mientras que V(m/s) la expresada en m/s. Por lo tanto se tendrá que:
|
V2 |
|
V(m/s)2 = |
|
|
|
3,62 |
|
O aproximadamente lo mismo que,
|
V2 |
|
V(m/s)2 = |
|
|
|
13 |
|
Por lo tanto, si se quiere obtener la resistencia al aire (Ra), pero expresada en función de la velocidad del vehículo en km/h, resultaría esta otra expresión:
Ra (kgf) = Ca · c · d · H · V2 / 13
donde aquí, la velocidad (V) está expresada en km/h.
La potencia necesaria para vencer la resistencia al aire se expresa mediante la siguiente formulación:
|
Ra · V |
|
Pa (C.V.) = |
|
|
|
270 |
|
Pero como Ra = Ca · c · d · H · V2 / 13, la anterior expresión quedaría como sigue:
|
Ca · c · d · H · V3 |
|
Pa (C.V.) = |
|
|
|
270 · 13 |
|
Resultando finalmente,
|
Ca · c · d · H · V3 |
|
Pa (C.V.) = |
|
|
|
3510 |
|
Por último, la RESISTENCIA TOTAL que se opone al movimiento del vehículo sería la suma de las anteriores resistencias calculadas, es decir:
RT (kgf) = Rr + Rp + Ra = QT · ( µr + i ) + Ca · c · d · H · V2 /13
Siendo la potencia necesaria para vencer la resistencia total al movimiento, la calculada por esta siguiente expresión:
|
RT · V |
|
PT (C.V.) = Pr + Pp + Pa = |
|
|
|
270 |
|
Donde V es la velocidad a la que circula el vehículo en km/h.
Recordar que el motor del vehículo deberá desarrollar una potencia mayor que la anteriormente expresada, para tener en cuenta las pérdidas que se producen a lo largo del sistema de transmisión. De esta forma, la potencia que deberá desarrollar el motor para superar la resistencia al movimiento del vehículo vendrá dada por la expresión:
|
PT |
|
PT,m = |
|
|
|
ηt |
|
Siendo ηt el rendimiento total del sistema de transmisión del vehículo.
5.3- Pendiente superable
Para realizar el cálculo de la pendiente superable por un vehículo en función de la velocidad que lleve en cada momento, se partirá de la expresión de la potencia que desarrolla el vehículo, ya conocida del apartado anterior:
|
RT · V |
|
PT (C.V.) = |
|
|
|
270 |
|
Siendo V la velocidad a la que circula el vehículo en km/h, y RT la resistencia total al movimiento que debe hacer frente.
Asimismo, esta resistencia al movimiento a que debe hacer frente el vehículo, se expresaba como:
RT (kgf) = Rr + Rp + Ra = QT · ( µr + i ) + Ca · c · d · H · V2 /13
En situaciones de circulación en carreteras con elevadas pendientes, y para el caso de vehículos industriales, camiones y furgones, la velocidad que llevan estos vehículos en estas circunstancias suele ser reducida.
De hecho, para velocidades inferiores a los 45 km/h, la resistencia del aire (Ra) es muy pequeña y por lo tanto el perfil aerodinámico del vehículo influye poco. En estas situaciones, es decir, circulando el vehículo a velocidades inferiores a los 45 km/h, la resistencia aerodinámica se puede considerar despreciable (Ra ≈ 0), y por tanto la resistencia total al movimiento quedaría como:
RT (kgf) = Rr + Rp = QT · ( µr + i )
Quedando entonces la potencia necesaria para vencer la resistencia total con la siguiente expresión:
|
QT · ( µr + i ) · V |
|
PT (C.V.) = |
|
|
|
270 |
|
Sin embargo, la potencia que debe desarrollar el motor (PT,m) deberá ser algo mayor para compensar las pérdidas que se originan en el sistema de transmisión:
|
PT |
|
PT,m = |
|
|
|
ηt |
|
Siendo ηt el rendimiento total del sistema de transmisión del vehículo, que suele estar comprendido entre 0,8 y 0,9.
Sustituyendo se tiene que:
|
QT · ( µr + i ) · V |
|
PT,m (C.V.) = |
|
|
|
270 · ηt |
|
Despejando la pendiente (i) de la expresión anterior, se obtendrá la pendiente superable por el vehículo según la potencia desarrollada por el motor (PT,m), el rendimiento del sistema de transmisión (ηt), de su peso total (QT), del coeficiente de rodadura (µr) y de la velocidad máxima que pueda desarrollar el vehículo para cada marcha (V):
|
270 · ηt · PT,m |
|
i = |
- µr |
|
|
QT · V |
|
Para la mayoría de vehículos industriales y comerciales, camiones y furgones, se recomienda que a potencia máxima del motor y con la relación máxima de marchas en la caja de cambio de velocidades, el vehículo sea capaz de superar una pendiente máxima mayor o igual al 22% (imáx ≥ 22%).
>> FIN DEL TUTORIAL
Volver a
Tutoriales
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055

