— Tutorial nº 84 —
Cálculo y Diseño de Cintas Transportadoras
Índice de contenidos:
1- Introducción
1.1- Generalidades
1.2- Ventajas en el uso de cintas transportadoras
2- Componentes principales de una cinta transportadora
2.1- Banda transportadora
2.2- Estaciones de rodillos
2.3- Tambor de reenvío
2.4- Tambor motriz
2.5- Tambores de inflexión
2.6- Elementos de encauzado
2.7- Estructura del bastidor
2.8- Motorreductor eléctrico y cableado
2.9- Dispositivos tensores
3- Parámetros que influyen en el diseño de una cinta transportadora
3.1- Velocidad de avance de la cinta
3.2- Anchura de la banda
3.3- Disposición de los rodillos
3.4- Ángulo de inclinación máxima de la cinta
3.5- Características del material a transportar
4- Procedimiento de cálculo de los parámetros de diseño de una cinta transportadora
4.1- Datos iniciales de diseño
4.2- Cálculo del área de la sección transversal del material transportado
4.3- Capacidad de transporte de la cinta
4.4- Potencia de accionamiento de la cinta
4.5- Resistencia mínima a tracción de la banda
4.6- Cálculo de las tensiones de trabajo de la banda
4.7- Cálculo del diámetro y velocidad de giro del tambor motriz
4.8- Cálculo de cargas sobre el tambor motriz
4.9- Selección final de la resistencia nominal de la banda
5- Ejemplo de cálculo de una cinta transportadora
ANEXOS:
Anexo nº 1.- Guía de ingeniería y diseño de cintas transportadoras
Anexo nº 2.- Catálogo técnico de componentes para cintas transportadoras
DESARROLLO DEL CONTENIDO
1- Introducción
1.1- Generalidades
Las cintas transportadoras constituyen un sistema muy empleado en la industria y en otros muchos sectores para realizar el transporte en continuo de materiales granulados, tales como cereales, carbón, minerales, tierras, etc., aunque también existen tipos especiales de cintas transportadoras adaptadas que se pueden usar para transportar personas o cosas. Por tanto, es posible encontrar en el mercado una amplia variedad de cintas transportadoras que difieren en su modo de funcionamiento, medio de trabajo, tipo de material que transporta y dirección de transporte.

Básicamente, una cinta transportadora consta de una banda continua que es arrastrada por fricción por la acción de un tambor cilíndrico, llamado tambor motriz, que es accionado, en la mayoría de las ocasiones, por un motor eléctrico, aunque pueden emplearse otras fuentes de energía para el accionamiento del tambor motriz.
La fricción necesaria que debe existir entre la superficie de la banda en contacto con el tambor y la superficie del propio tambor se consigue, bien recubriendo la superficie del tambor con un forro que mejore la fricción con la banda, o bien aplicando una cierta tensión a la banda transportadora, habitualmente mediante un mecanismo tensor formado por un husillo o un tornillo tensor, o utilizando contrapesos.
Es importante saber que en el momento de arranque de la cinta se produce en el motor de accionamiento un par motriz superior al nominal, que genera una gran fuerza tangencial en la periferia del tambor motriz. Para que esta fuerza tangencial se trasmita correctamente a la banda y se ponga en marcha, es necesaria que exista una cierta tensión en la banda que evite su resbalamiento sobre el tambor en los momentos iniciales de la puesta en marcha.
El otro tambor del que suele constar una cinta transportadora debe girar libre, sin ningún tipo de accionamiento, y su función es la de servir de retorno a la banda. La banda es soportada por estaciones de rodillos situados entre los dos tambores, o también, aunque menos frecuente, por una chapa continua o de algún otro material que ofrezca muy baja fricción, dispuesto a modo de cuna sobre la que se apoye la banda transportadora.
El transporte del material se consigue debido al movimiento de la banda que se mueve en dirección al tambor situado en la cabeza de la cinta, que es donde la banda gira y da la vuelta, moviéndose entonces en sentido contrario hacia el otro tambor. Cuando el material que lleva la cinta alcanza el final, la banda, al darse la vuelta, hace que el material transportado por la banda sea vertido fuera de la misma debido a la acción de la gravedad y/o de la inercia.
1.2- Ventajas en el uso de cintas transportadoras
Cada vez más, el transporte y trasiego de materiales supone un factor importante a tener en cuenta en la rentabilidad económica de cualquier actividad, ya sea industrial, minera, agrícola o de cualquier otra índole. Se estima que en algunos sectores, los gastos de transporte pueden suponer entre el 40-50% los gastos de explotación, por lo que se hace necesario seleccionar de manera eficiente el tipo de transporte más adecuado a cada situación.
Las cintas transportadoras es un sistema de trasiego de materiales que se puede encuadrar dentro de los tipos de transporte de materiales en continuo. Su gran capacidad de transporte y adaptación al tipo de terreno, entre otras muchas ventajas que más adelante se mencionarán, hacen de la cinta trasportadora un medio de transporte muy empleado en la industria, y en otros muchos sectores, como la minería, la agricultura, el sector naval, logístico, etc., debido también a su facilidad de diseño y fabricación, y también a su probada rentabilidad económica.
A continuación, se destacarán las ventajas que han fomentado durante los últimos años el uso de las cintas transportadoras como un sistema de transporte ideal para el manejo de materiales:
- Capacidad de transporte:
Una de las ventajas que más influye en la elección de cintas transportadoras para el transporte en continuo de materiales es su gran capacidad de transporte, muy superior al de otros sistemas.
Por ejemplo, una cinta transportadora de 1,5 m de ancho, moviéndose a una velocidad de 3,3 m/s, ofrece una capacidad de transporte de más de 6.000 t/h para un material común que tenga una densidad entorno a 1,7 t/m3. Con estas cifras, ningún otro sistema actual es capaz de hacerlo de una manera tan rápida y eficiente.
- Adaptación al perfil del terreno y versatilidad:
Otra de las características de las cintas transportadoras es que pueden seguir el perfil natural del terreno, incluso con pendientes relativamente altas, dependiendo del tipo de material a transportar, lo que hace que su uso sea muy extendido en trabajos de minería o en trabajos de excavación o vaciado de tierras.
Además el uso de cintas transportadoras permite diseñar líneas de transporte de material que puede adaptarse a cualquier tipo de configuración o implantación de procesos productivos en industrias, almacenes, etc.
En este sentido, cualquier cinta transportadora permite la posibilidad de poder tener múltiples puntos de alimentación y descarga, según las necesidades de cada proyecto, lo que permite optimizar los tiempos de producción de cualquier proceso industrial.

- Bajos consumos de energía:
Está demostrado que las cintas transportadoras consumen menos energía por tonelada de material transportado que otros sistemas de transporte.
Además, aunque la mayoría de las cintas transportadoras son accionadas por un motor eléctrico, su versatilidad de diseño permite usar otras fuentes de energía (motor de combustión, de gas natural, energía hidroeléctrica o solar) que accione el tambor motriz de la cinta.
- Degradación mínima del material transportado:
Otro de los aspectos que más interesa es que el material transportado sufra el mínimo deterioro durante el transporte. El uso de cintas transportadora asegura un transporte suave que hace que el material transportado sufra una degradación mínima o prácticamente inapreciable.
Además, la propia configuración de una cinta transportadora permite utilizar elementos de cubierta que protejan de la intemperie (lluvia, nieve, sol, viento) al material transportado o a la propia cinta, mejorando su estado de conservación y durabilidad.
- Fácil tarea de mantenimiento:
El proceso de reparación o reemplazo de cualquier componente de una cinta transportadora es una tarea que suele ser fácil y rápida, que no exige de gran especialización, lo que abarata mucho el coste de mantenimiento de este tipo de instalaciones.
2- Componentes principales de una cinta transportadora
2.1- Banda transportadora
La banda transportadora es el elemento flexible encargado de transportar los materiales desde el punto de carga de la cinta hasta el otro extremo donde se realiza la descarga del material transportado. Existen numerosos tipos de bandas transportadoras en el mercado, cada uno adaptado al tipo de material a transportar y de las condiciones de trabajo de la cinta.
La banda transportadora de una cinta es un elemento que, por la función que desempeña, deberá ser capaz de soportar la acción de distintas solicitaciones como:
- Las fuerzas longitudinales derivadas del esfuerzo tangencial del tambor motriz que hace mover a la cinta transportadora, y del esfuerzo de tensado de la cinta;
- El peso del material transportado, así como los impactos derivados de la caída del material sobre la cinta en el punto de carga, que va a generar erosiones en la superficie de la banda;
- Los agentes externos (climatológicos o del ambiente de trabajo) que pueden atacar y degradar las propiedades del material de fabricación de la cinta.

Para poder soportar con garantías todas estas acciones, la banda de una cinta transportadora se suele fabricar de dos componentes principales:
• Un tejido interior resistente que transmite los esfuerzos derivados del peso de la carga y de la acción del tambor motriz
• Una serie de recubrimientos exteriores que protege a la banda de la erosión e impactos.
El tejido es el componente interior de la banda y es el encargado de transmitir y soportar los esfuerzos. Consta de un entramado de hilos en sentido longitudinal o urdimbre, y de una trama o hilos en sentido trasversal, conformando el conjunto el tejido interior de la banda.
La urdimbre son los encargados de soportar los esfuerzos longitudinales de tracción que son los más importantes, por lo que serán hilos más resistentes que los hilos transversales de la trama, los cuales sólo soportarán esfuerzos transversales, que son secundarios y de menor cuantía que los longitudinales. Además, la rigidez transversal de la trama no deberá ser tampoco excesiva, para que la banda pueda adaptarse bien a la forma en artesa en la que se disponen los rodillos.
A continuación se incluye una tabla con los principales tipos de tejidos empleados para la fabricación de bandas:
Tabla 1. Tejidos empleados en bandas transportadoras |
|
Tipo de Tejido |
Designación |
Algodón |
B |
Rayón |
Z |
Poliéster |
E |
Poliamida |
P |
Cables de acero |
St |
Por otro lado, los recubrimientos conforman la parte externa de la banda, tanto por encima como por debajo de la misma, protegiendo al tejido interior. Su espesor será función del tipo de aplicación y de la anchura de fabricación de la banda.
Los materiales que se usan para los recubrimientos de bandas son principalmente de tipo elastómeros (caucho natural) o plastómeros (PVC), aunque últimamente están apareciendo otros nuevos materiales compuestos. No obstante, la goma es el elemento básico de los recubrimientos en cintas transportadoras.
Los valores mínimos necesarios de resistencia a la tracción, alargamiento de rotura longitudinal y abrasión de los distintos materiales que pueden emplearse en la fabricación de las bandas transportadoras están recogidos en las normas DIN 22102 y 22131, estableciéndose las categorías W, X, Y, Z, como se indican en la siguiente tabla.
Tabla 2. Propiedades mecánicas de los recubrimientos de bandas transportadoras |
||||
Tipos de recubrimientos |
W |
X |
Y |
Z |
Resistencia a la tracción longitudinal (N/mm2) |
18 |
25 |
20 |
15 |
Alargamiento de rotura longitudinal (%) |
400 |
450 |
400 |
350 |
Abrasión (mm3) |
90 |
120 |
150 |
250 |
También es posible encontrar en alguna literatura técnica que, según el uso o propiedades de la banda, éstas también pueden designarse con la nomenclatura que se recoge en la siguiente tabla:
Tabla 3. Designación de bandas transportadoras |
|
Designación |
Características de la banda |
E |
Propiedades antiestáticas |
K |
Propiedades antiestáticas y resistente a la llama |
S |
Resistente a la llama con o sin propiedades antiestáticas |
T |
Resistentes al calor |
R |
Resistentes al frío |
G |
Resistente a la presencia de aceites y grasas |
A |
Apta para el transporte de alimentos |
C |
Destinada al transporte de productos químicos |
2.2- Estaciones de rodillos
Las estaciones de rodillos soportan el peso de la cinta y, al estar montados sobre rodamientos, giran solidarios al movimiento de la cinta, facilitando así su desplazamiento. Suelen disponerse de varias estaciones de rodillos espaciadas una distancia que dependerá del tipo de cinta y la carga a transportar, y que más adelante se mostrará cómo calcular.
Dependiendo de la posición que ocupen los rodillos en la cinta, éstos pueden ser de distintos tipos acorde a la función que van a desempeñar. En este sentido, en una cinta transportadora se pueden distinguir:
- Rodillos superiores
- Rodillos inferiores
- Rodillos amortiguadores

Las estaciones de rodillos superiores se sitúan en la parte superior del bastidor de la cinta, y son los que soportan el peso de la cinta y de la carga que transporta.
Normalmente las estaciones de rodillos superiores están formadas por una alineación de tres rodillos que adoptan una forma de "artesa", donde los rodillos exteriores se sitúan inclinados entorno a 35º mientras que el rodillo central se sitúa en una posición horizontal.
Esta disposición en artesa de los rodillos superiores sirve para dotar a la banda transportadora de una cierta geometría cóncava que mejora el transporte de la carga y evita su derrame al exterior.
No obstante, las bandas transportadoras suelen cambiar a una forma plana en los extremos, con objeto de favorecer mejor las operaciones de carga y descarga del material sobre la cinta, que eviten derrames de material fuera de la misma.
Por tanto, en la primera y la última estación, que son estaciones de transición, los rodillos de los extremos se disponen con una menor inclinación, en torno a 22º, con objeto de favorecer la transición de la banda de forma de artesa a forma plana.
También conviene decir que la distancia de las estaciones de rodillos superiores se reduce en las zonas próximas a los puntos donde se realizan la carga y descarga de material, debido a que son zonas de mayor solicitación de la cinta y necesitan de una mayor resistencia.

Por otro lado, las estaciones de rodillos inferiores se sitúan en la parte inferior del bastidor de la estructura soporte de la cinta.
La banda transportadora se desplaza en su tramo de retorno a través de los rodillos inferiores, que sirven para sostener la cinta y facilitar su movimiento.
Las estaciones de rodillos inferiores suelen estar compuestos por un solo rodillo plano dispuesto a todo lo ancho de la cinta.
Estos rodillos, al estar situado en el tramo de retorno de la cinta, soportan sólo el peso de la banda transportadora que va vacía, por lo que se pueden situar más espaciados unos de otros.
Como ya se ha comentado anteriormente, en una cinta transportadora suelen disponerse normalmente de varias estaciones de rodillos, espaciados unos de otros una distancia que dependerá del tipo de cinta, su anchura y la carga del material que transporta.
De manera orientativa, se adjunta la siguiente tabla del fabricante ULMA, donde se incluyen los valores usuales de separación entre estaciones de rodillos:
Tabla 4. Distancias de separación entre estaciones de rodillos (m) |
|||
Ancho de banda |
Rodillos Superiores |
Rodillos Inferiores |
|
Peso específico del material (t/m3) |
|||
≤ 0,6 |
> 0,6 |
||
400 |
1,35 |
1,35 |
3,00 |
500 |
1,35 |
1,20 |
3,00 |
650 |
1,20 |
1,10 |
3,00 |
800 |
1,20 |
1,00 |
3,00 |
1.000 |
1,00 |
1,00 |
3,00 |
1.200 |
1,00 |
1,00 |
3,00 |
1.400 |
1,00 |
1,00 |
3,00 |
1.600 |
1,00 |
1,00 |
3,00 |
1.800 |
1,00 |
1,00 |
3,00 |
> 2.000 |
1,00 |
1,00 |
2,40 |
En la zona de carga de la cinta, debido al impacto que se produce al caer el material sobre la cinta, se suelen disponer de un tipo especial de rodillos, llamados rodillos amortiguadores.

Los rodillos amortiguadores tienen la función de amortiguar el impacto del material al caer sobre la cinta, por lo cual, este tipo de rodillos sólo se encuentra en esta posición de la cinta.
Los rodillos amortiguadores son fáciles de identificarlos y se pueden diferenciar del resto por su forma geométrica, ya que contienen unas ranuras en su superficie para favorecer la absorción de energía, y suelen estar recubiertos de caucho.
Evidentemente al estar más solicitados, la distancia entre estaciones de rodillos amortiguadores será menor, y dependerá del tipo de material a transportar, la altura de caída del material sobre la cinta y la velocidad de la banda transportadora.
2.3- Tambor de reenvío
El tambor de reenvío está situado generalmente en el inicio de la instalación, al lado opuesto respecto a la posición que ocupa el tambor motriz. El tambor de reenvío tiene la función de permitir el retorno de la banda transportadora hacia el otro extremo de la cinta donde se encuentra, como se ha dicho, el tambor motriz.
Se trata de un tambor liso y contiene un rascador de tipo triangular montado con un vértice sobre el eje de la cinta para favorecer el efecto flector. Este elemento permite limpiar la cinta por el interior antes de entrar en contacto con el tambor, con el fin de evitar daños en el mismo.
2.4- Tambor motriz

El tambor motriz está situado generalmente en la cabeza de la cinta, al lado opuesto del tambor de reenvío, y es el encargado de transmitir el movimiento de traslación a la cinta.
Generalmente, el tambor motriz es accionado por un motorreductor eléctrico acoplado al eje del tambor, o a través de una transmisión de poleas, aunque también puede ser accionado por otros tipos de motores, por ejemplo, motores de combustión.
Por lo general, el tambor motriz se dispone con la superficie engomada, de manera que favorezca el contacto entre el tambor y la banda, con el objetivo de evitar que se produzca resbalamiento de ésta sobre la superficie del tambor.
Mediante un sistema de varillas roscadas se puede regular la posición exacta del tambor motriz y con ello, la presión que se establece entra las superficies del tambor y la cinta, con objeto de favorecer un buen contacto y evitar, como se ha dicho, el resbalamiento entre superficies.
Además, el tambor motriz suele disponer de un rascador de láminas con brazos de reacción graduables y rasquetas metálicas endurecidas que permite realizar labores de limpieza de la banda por el exterior.
2.5- Tambores de inflexión
Para cintas transportadoras provistas de contrapesos para el tensado de la cinta, en el bastidor de contrapeso se sitúan los tambores de inflexión. Son dos los tambores de inflexión que tienen la función de cambiar la dirección de la cinta, de manera que conducen a la cinta hacia el sistema de contrapeso vertical de la instalación.
2.6- Elementos de encauzado
Un elemento importante que impide que se salga material de la cinta, sobre todo durante el proceso de descarga sobre la cinta, es el elemento de encauzado. Éste suele estar realizado generalmente de chapa metálica y se encuentra unido directamente al bastidor de la cinta con el objeto de impedir que se produzcan pérdidas de material por los laterales de la cinta.

Aunque este elemento se puede instalar a lo largo de todo el recorrido de la cinta, se suele colocar sobretodo en la zona de descarga de material sobre la cinta, por ser mayor el riesgo de derrame de material, aunque también se puede instalar en otras zonas donde se considere que existe riesgo de producirse algún derrame de material por los laterales.
Por tanto, este elemento de encauzado se suele situar a ambos lados de la cinta en los primeros metros de recorrido, y va a ayudar a impedir que fragmentos de material salgan fuera de la banda transportadora al rebotar durante la descarga.
El dispositivo de encauzado se suele unir por medio de una fijación mecánica al bastidor que soporta la cinta, mediante el empleo de perfiles metálicos que lo sujetan y lo elevan unos centímetros para evitar que se apoye directamente en la banda.
En la parte inferior del elemento de encauzado, donde se produce el encuentro con la banda transportadora, se suele colocar una tira de goma o espuma que evite el contacto directo de la chapa del elemento de encauzado con la banda. Con ello se evita que se produzca rozamiento entre la banda y la chapa metálica del elemento de encauzado que pueda dañar a la propia banda, al mismo tiempo que impide que se pierda material por ese espacio.
2.7- Estructura del bastidor
El bastidor lo constituye el entramado metálico de perfiles estructurales, generalmente de acero, que sostiene a la cinta transportadora y a todos los demás elementos y componentes que constituyen el sistema.
La estructura del bastidor se adapta al medio de trabajo según la zona donde la cinta se ubique y el tipo de servicio que realice. En la zona donde se produce la descarga de material sobre la cinta, el bastidor suele adaptarse mediante un entramado y geometría diferente de perfiles estructurales. En este primer tramo de la cinta, la estructura del bastidor deberá diseñarse para sustentar a los diversos componentes que se suelen instalar en esta zona de la cinta, como son los rodillos amortiguadores con sus estaciones correspondientes, el tambor de reenvío, el elemento de encauzado, rodillos inferiores, rascador, además de la parte proporcional de la cinta.
Otra geometría de bastidor más liviana se emplea para el cuerpo central de la cinta y que abarca el mayor tramo de recorrido. El bastidor del cuerpo central sustenta la mayor proporción de recorrido de la cinta, además de las estaciones de rodillos, por lo que el diseño debe realizarse de tal manera que optimice el peso de la estructura, sin penalizar su estabilidad y resistencia.
Por último, el bastidor motriz es la estructura soporte que se encuentra sólo en la parte final del recorrido de la cinta. Esta parte del bastidor sustenta tanto a los rodillos superiores como al tambor motriz, rodillos inferiores, rascador de láminas, así como el equipo motorreductor, además de la parte proporcional correspondiente al tramo final de la cinta.
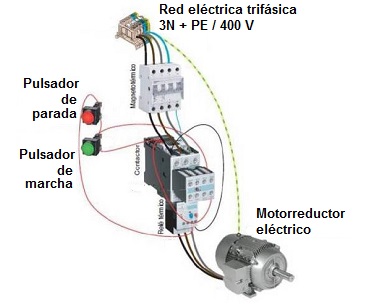
2.8- Motorreductor eléctrico y cableado
Para el accionamiento del tambor motriz que mueve la cinta, se suele emplear un motor eléctrico dotado de un reductor de velocidad cuyo eje de salida engrana con el eje del tambor motriz de la cinta.
Como toda instalación eléctrica, se hace necesario dotar al sistema del correspondiente cableado eléctrico que conecte con la fuente de alimentación y sirva de conexión entre todos los componentes eléctricos que componen el sistema, como son los pulsadores de marcha y parada, además de los dispositivos de mando y protección necesarios para que la instalación sea segura.
En la figura adjunta se representa un esquema típico de la instalación eléctrica que gobierna la instalación de una cinta transportadora sencilla.
2.9- Dispositivos tensores
Para que una cinta transportadora funcione correctamente es necesario asegurar una cierta tensión mínima en los ramales de la banda durante su funcionamiento. En la mayoría de los casos, cuando la cinta no es demasiado larga esta tensión se consigue con el reglaje en el posicionamiento de los tambores de reenvío y motriz.
Pero no siempre es posible asegurar esta tensión en todo momento en los ramales de la banda durante el funcionamiento de la cinta. Así, para aquellos casos en los que se empleen cintas transportadoras de cierta longitud, o cuando el peso de la mercancía que se transporte sea grande en relación al módulo elástico del material de la banda, o cuando la carga fluctúe muy rápidamente durante el transporte, se recomienda utilizar dispositivos tensores adicionales que aseguren siempre una cierta tensión en los ramales de la banda.
De esta manera, con ciertos sistemas activos de tensado de fuerza constante, los cambios en la longitud de la cinta que se produzcan durante el servicio se compensan automáticamente, impidiéndose así que se produzca el destensado de la banda.
Por lo tanto, parece obvio que estos dispositivos deban diseñarse y construirse para ser capaces de compensar estos cambios de longitud durante el funcionamiento normal de la cinta, así como para regular la longitud de la cinta a la tensión inicial requerida.
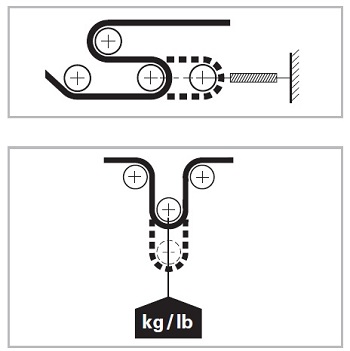
El tensado de la cinta mediante fuerza constante se logra, normalmente, empleando dispositivos tensores que funcionan mediante el tensado por resorte o mediante tensores neumáticos o hidráulicos.
En el caso de cintas pesadas o de transportadores largos se suelen emplear un sistema de contrapesos, que funciona como un sistema tensor por gravedad, y que permite proporcionar un tensado de la cinta de fuerza constante.
La función principal del sistema de contrapesos es la de establecer y mantener una tensión predeterminada en la banda de la cinta necesaria para que el tambor motriz pueda transmitir el movimiento de traslación a la cinta, sin que se produzca un excesivo resbalamiento entre superficies que haría más dificultoso el avance de la cinta.
Además, con el uso de contrapesos, también se pueden eliminar la acumulación de holguras en la banda que se producen durante el arranque o durante sobrecargas momentáneas, además de proporcionar una reserva de longitud de banda suficiente para poder realizar nuevos empalmes en caso de ser necesario.
Básicamente, un sistema de contrapesos está compuesto por unos perfiles metálicos verticales que sirven de guía a una caja rellena de tierra, piedras o grava que hace la función de contrapeso.
La estructura generalmente está fijada a tierra, pero presenta una articulación que permite el movimiento vertical del conjunto de elementos que integran el sistema de contrapeso de la cinta.
3- Parámetros que influyen en el diseño de una cinta transportadora
3.1- Velocidad de avance de la cinta
Uno de los factores que más influye en la capacidad de transporte de una cinta es la velocidad de avance (v) de la banda. En general, la velocidad de avance de una cinta va a depender del tipo de material que se transporte, de manera que la velocidad máxima de avance de una cinta transportadora va a estar limitada por el tipo de material transportado.
Además, conocer la velocidad de avance de una cinta es necesario para poder establecer un ritmo de descarga adecuado de material sobre la cinta, de manera que no se origine el agolpamiento del material en el lugar de alimentación de la cinta.
Asimismo, en general una cinta transportadora podrá trabajar a más velocidad de avance conforme aumenta la anchura de la banda, ya que en cintas más anchas el porcentaje del material en contacto con la banda resulta menor que en las cintas más estrechas, ocasionando así menos desgaste de la banda.
La siguiente expresión permite conocer la capacidad de transporte o capacidad volumétrica de transporte de una cinta:
Qv = 3600 · v · A · k
siendo,
Qv : Capacidad volumétrica de la banda (m3/h)
v : Velocidad de avance de la banda (m/s)
A : Área de la sección transversal del material transportado por la banda (m2)
k : Coeficiente de reducción de la capacidad de transporte de la cinta por su inclinación. Si la cinta transportadora está inclinada, ya sea de forma ascendente o descendente, se le debe aplicar este factor de reducción del área transversal del material transportado. Este coeficiente se puede calcular aplicando la siguiente expresión:
k = 1 - 1,64 · ( |
φ · π |
)2 |
| 180 |
donde,
φ : es el ángulo de inclinación de la cinta (º)
3.2- Anchura de la banda
Es evidente que la anchura de la banda también influye directamente sobre la capacidad de transporte de una cinta. Aunque no hay una norma fija que ayude a determinar a priori el ancho de banda de una cinta, parece lógico pensar que el tamaño máximo predominante de los trozos del material que vaya a transportar la cinta influya en la elección de su ancho de banda.
Por lo general, y a raíz de los resultados de la buena práctica en el uso de cintas transportadoras, se suele fijar el ancho de banda de tal manera que éste sea mayor, por lo menos, a cinco o seis veces el tamaño de los trozos que predomine en el material, y siempre se recomienda que el ancho de banda sea mayor a cuatro veces el tamaño de los mayores trozos que contenga el material.
Anchura de la banda > 5,5 · tamaño trozos predominantes
A continuación, se representa una sección transversal típica que tiene el material sobre la banda de una cinta transportadora con una configuración de rodillos en artesa:
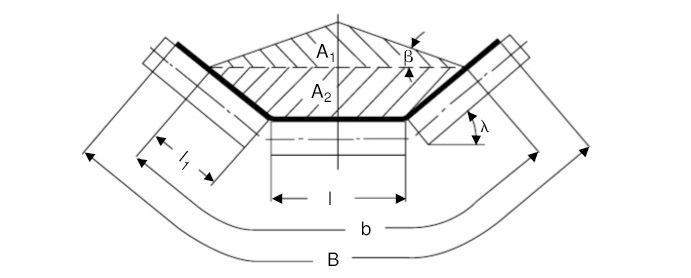
La sección transversal (A) del material sobre la banda se puede calcular mediante la siguiente expresión matemática derivada de la figura anterior:
A = A1 + A2
donde,
A1 = 0,25 · tan(β) · [ l + (b - l) · cos(λ) ]2
A2 = l1 · sen(λ) · [ l + l1 · cos(λ) ]
siendo,
b = 0,9 · B - 0,05
l1 = 0,5 · (b - l)
3.3- Disposición de los rodillos
La disposición de los rodillos bajo la banda es fundamental para conseguir una sección transversal de material óptima, y mejorar la capacidad de transporte de la cinta.
En general, esta disposición puede hacerse en forma horizontal empleando juegos de tres a cinco rodillos formando una cuna o abarquillamiento con objeto de dotar de cierta concavidad a la sección de la banda. La separación entre filas de rodillos dependerá del ancho de la cinta y del peso específico del material transportado.
En la zona de descarga del material sobre la cinta, los rodillos deberán ir colocados a distancias mucho más próximas. Sin embargo, es importante que los rodillos no estén exactamente debajo de la zona de descarga del material, ya que se produciría un martilleo continuo sobre la cinta. Además, se recomienda situar en esta zona rodillos amortiguadores ranurados, de manera que absorban la energía y amortigüen el impacto producido por el material al caer sobre la cinta.
Además, también se suelen emplear rodillos guía laterales que se colocan en la cinta para facilitar el guiado de la banda en su continuo movimiento de avance.
3.4- Ángulo de inclinación máxima de la cinta
Otro parámetro que es muy importante conocer es el ángulo de máxima inclinación que puede tener una cinta transportadora para aquellos casos donde la cinta no tiene una posición horizontal, o tenga tramos con una inclinación ascendente o descendiente.
En este caso interesa conocer cuál es la inclinación máxima que se le puede dar a la cinta para que el transporte de un determinado material se pueda realizar con seguridad, y sin que se produzcan desprendimientos o caídas de trozos de material.
Evidentemente la inclinación máxima que puede adoptar una cinta dependerá del tipo de material que transporte, estando el valor de este parámetro determinado por el grado de fricción que se establezca entre el material y la banda. En cualquier caso, el ángulo de inclinación máxima de la cinta deberá ser menor que el llamado ángulo de sobrecarga del material que transporte.
A continuación, se incluye la siguiente tabla que permite determinar el ángulo de máxima inclinación de la cinta transportadora en función del tipo de material que transporta:
Tabla 5. Ángulo de la máxima inclinación de una cinta transportadora |
|
Material |
Inclinación máxima de la cinta |
Arcilla fina |
15º |
Arena seca |
16º - 18º |
Asfalto |
16º - 18º |
Basalto |
18º |
Caliza |
18º |
Cemento |
18º - 20º |
Cenizas de carbón |
20º |
Cobre |
20º |
Coque |
18º |
Cuarzo |
18º |
3.5- Características del material a transportar
A la hora de diseñar una cinta transportadora resulta muy importante tener en cuenta las diferentes características del tipo de material que va a ser transportado por la cinta.
Entre las características del material que interesa saber están el tamaño y forma del material, su peso específico, el valor del ángulo de reposo y de sobrecarga, si es o no un material abrasivo, o la temperatura que tendrá el material al entrar en contacto con la banda.
A continuación se describe la influencia de cada una de las anteriores propiedades en el diseño de una cinta transportadora:
- Tamaño del material
El tamaño del material que transporte una cinta influye en la elección del ancho de banda de la cinta. Evidentemente, a mayor tamaño de los trozos que conforman el material transportado, mayor anchura tendrá que tener la banda transportadora para evitar derrames de material por lo laterales de la banda.
Por lo general, y a raíz de los resultados de una buena práctica en el uso de cintas transportadoras, se suele fijar el ancho de banda de tal manera que éste sea mayor, por lo menos, a cinco o seis veces el tamaño de los trozos que predomine en el material, y se recomienda que el ancho de banda sea siempre mayor a cuatro veces el tamaño de los mayores trozos que contenga el material.
Anchura de la banda > 5,5 · tamaño trozos predominantes
- Peso específico
La capacidad de transporte de una cinta transportadora depende en gran medida del valor del peso específico del material que transporte, como se verá más adelante en el proceso de cálculo de la capacidad de transporte en masa de una cinta.
Para disponer de datos de los pesos específicos de materiales, se adjunta el siguiente enlace a otra sección de esta web donde se puede consultar los pesos específicos de distintos materiales que se incluyen en la lista:
›› Pesos Específicos de Materiales
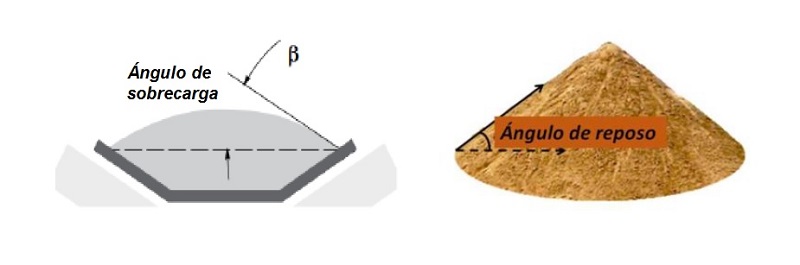
- Ángulo de reposo y ángulo de sobrecarga
Dos parámetros muy importantes que van a condicionar en gran medida el diseño de una cinta transportadora son el ángulo de reposo y el ángulo de sobrecarga del material que transporte la cinta.
El ángulo de reposo de un material es el ángulo que se forma al verter el material desde una cierta altura, es decir, es el máximo ángulo posible que se forma para la pendiente de una acumulación de material.
En un material granuloso cualquiera, el ángulo de reposo está determinado por la fricción, la cohesión y la forma de las partículas, pero en los materiales granulares sin cohesión, donde las partículas son muy pequeñas en relación al tamaño del conjunto acumulado, el ángulo de reposo coincide con el ángulo de rozamiento interno o ángulo de fricción del material granular.
Por otro lado, el ángulo de sobrecarga del material es el ángulo que forma la superficie del material respecto al plano horizontal sobre la cinta en movimiento.
A continuación, se incluye una tabla resumen con las principales características de los materiales que son necesarias conocer para iniciar el diseño de una cinta transportadora:
Tabla 6. Características de los materiales |
|||
Material |
Peso específico (t/m3) |
Ángulo de reposo (º) |
Abrasividad |
Arcilla fina |
1,0 - 1,6 |
- |
Muy abrasiva |
Arena seca |
1,5 - 1,8 |
35 |
Muy abrasiva |
Asfalto |
0,75 |
30 - 45 |
Abrasivo |
Basalto |
1,4 - 1,7 |
27 - 35 |
Abrasivo |
Caliza |
1,3 - 1,5 |
38 |
Abrasivo |
Cemento |
1,3 - 1,5 |
30 - 40 |
Muy abrasivo |
Cenizas de carbón |
0,7 - 0,8 |
45 |
Poco abrasivo |
Cobre |
1,9 - 2,2 |
20 |
Muy abrasivo |
Coque |
0,5 - 1 |
30 - 45 |
Muy abrasivo |
Cuarzo |
1,3 - 1,45 |
20 - 29 |
No abrasivo |
Granito |
1,4 - 1,5 |
35 |
Muy abrasivo |
Grava |
1,5 - 1,7 |
32 |
Muy abrasiva |
Harina |
0,6 - 0,9 |
0 - 10 |
No abrasiva |
Fosfatos |
1 |
26 |
Abrasivo |
Lignito |
0,7 - 1 |
40 |
Abrasivo |
Tierra |
1,2 - 1,3 |
35 |
- |
Trigo |
0,75 |
25 |
No abrasivo |
Cebada |
0,65 |
25 |
No abrasivo |
Avena |
0,45 |
30 |
No abrasivo |
- Temperatura
La temperatura del material que está en contacto con la banda es también un parámetro importante a tener en cuenta, dado que va a influir en la elección del tipo y la calidad de los recubrimientos de la banda, y también en la vida útil de los rodillos y tambores.
4- Procedimiento de cálculo de los parámetros de diseño de una cinta transportadora
4.1- Datos iniciales de diseño
Como datos de partida en el proceso de diseño de una cinta transportadora se suelen disponer de los siguientes:
• Tipo de material de transporte
• Longitud de la cinta (L, en m)
• Ángulo de inclinación de la cinta (φ en º)
• Ancho de banda disponible (B, en mm)
• Velocidad de avance de la cinta (v, en m/s)
A partir de los datos anteriores y haciendo uso de las formulaciones y tablas que se incluyen a continuación, se procede a mostrar paso a paso cómo realizar el cálculo de los parámetros de diseño de una cinta transportadora.
4.2- Cálculo del área de la sección transversal del material transportado
Para calcular el área de la sección transversal del material de transporte, se realiza una aproximación de la sección real a una teórica compuesta del área trapezoidal y triangular indicado en la figura siguiente, considerando que la cinta dispone de una configuración típica de rodillos en artesa.

La sección transversal (A) del material que simula a la sección real que forma el material se puede calcular sumando la sección trapezoidal y triangular de la figura anterior:
A = A1 + A2
donde,
A1 = 0,25 · tan(β) · [ l + (b - l) · cos(λ) ]2
A2 = l1 · sen(λ) · [ l + l1 · cos(λ) ]
siendo,
b = 0,9 · B - 0,05
l1 = 0,5 · (b - l)
Cada uno de los símbolos y letras anteriores tienen el significado siguiente:
A1 : es la sección triangular superior del material (m2)
A2 : es la sección trapezoidal inferior del material (m2)
β : es el ángulo de sobrecarga (º)
λ : es el ángulo de artesa en que se disponen los rodillos (º)
l : es la longitud de los rodillos (m)
B : es el ancho de banda de la cinta (m)
4.3- Capacidad de transporte de la cinta
La capacidad de transporte de una cinta es un dato técnico que siempre será preciso conocer. Esta capacidad de transporte se puede calcular haciendo uso de la siguiente fórmula:
Qv = 3600 · v · A · k
donde,
Qv : es la capacidad de transporte volumétrica de la banda (m3/h)
v : es la velocidad de avance de la banda (m/s)
A : es el área de la sección transversal del material, que se calcula según lo indicado en el apartado anterior (m2)
k : es un coeficiente de reducción de la capacidad de transporte por inclinación de la cinta. Si la cinta está inclinada, ya sea de forma ascendente o descendente, su capacidad de transporte disminuye, por lo que es necesario aplicar este factor k de reducción del área transversal. Este coeficiente se puede calcular aplicando la siguiente expresión:
k = 1 - 1,64 · ( |
φ · π |
)2 |
| 180 |
donde,
φ : es el ángulo de inclinación de la cinta (º)
La anterior expresión calcula la capacidad de transporte volumétrica, expresado en m3/h de material transportado, pero en multitud de ocasiones interesa conocer la capacidad de transporte de una cinta expresado en toneladas/hora (t/h). Para ello, será necesario conocer el peso específico (γ) del material transportado por la cinta.
Qm = Qv · γ
donde,
Qm : es la capacidad de transporte en masa de la banda (t/h)
Qv : es la capacidad de transporte volumétrica de la banda (m3/h)
γ : es el peso específico del material transportado (t/m3)
4.4- Potencia de accionamiento de la cinta
La potencia total de accionamiento de una cinta transportadora resulta ser la suma de las tres potencias parciales que se enumeran a continuación:
• P1: Potencia necesaria para mover la cinta en vacío y cargada, con desplazamiento horizontal de la cinta.
• P2: Potencia necesaria para elevar la carga hasta una cierta altura.
• P3: Potencia necesaria para vencer rozamientos de elementos auxiliares, dispositivos de limpieza y guías.
A continuación, se procederá a describir cómo realizar el cálculo de cada una de las anteriores potencias parciales:
1.- Potencia necesaria para mover la cinta en vacío y cargada con desplazamiento horizontal de la cinta (P1):
La primera potencia que es necesaria calcular es la potencia para mover la cinta, tanto en vacío como cargada, y con desplazamiento horizontal de la banda.
En este caso, la potencia se emplea para vencer el peso propio de la banda, del material que transporta y el rozamiento de los distintos tambores y rodillos presentes en el diseño de la cinta.
Para el cálculo de esta potencia se puede emplear la siguiente fórmula de cálculo:
P1 = |
Cb · v + Qm |
Cl · Kf |
donde,
Cb : es el factor de anchura de la banda (kg/s)
v : es la velocidad de avance de la banda (m/s)
Qm : es la capacidad de transporte en masa de la banda (t/h)
Cl : es el factor de longitud de la banda (m-1)
Kf : es el factor de servicio (-)
A continuación, se incluyen las siguientes tablas de donde se pueden extraer los valores de los distintos factores empleados en la formulación anterior de cálculo.
Tabla 7. Factor de ancho de la banda, Cb |
||||||||
|
Ancho de banda (mm) |
|||||||
Peso específico |
300 |
400 |
500 |
650 |
800 |
1000 |
1200 |
1400 |
γ ≤ 1 |
31 |
54 |
67 |
81 |
108 |
133 |
194 |
227 |
1 < γ ≤ 2 |
36 |
59 |
76 |
92 |
126 |
187 |
277 |
320 |
γ > 2 |
- |
65 |
86 |
103 |
144 |
241 |
360 |
414 |
Tabla 8. Factor de longitud de la banda, Cl |
|||||||||||
Longitud de banda (m) |
32 |
40 |
50 |
63 |
80 |
90 |
100 |
150 |
200 |
250 |
300 |
Cl |
222 |
192 |
167 |
145 |
119 |
109 |
103 |
77 |
63 |
53 |
47 |
Tabla 9. Factor de servicio, Kf |
|
Condiciones de trabajo |
Kf |
Favorables, buena alimentación, bajas velocidades |
1,17 |
Normal, condiciones estándar |
1 |
Desfavorables, baja temperatura y alta velocidad |
0,74 - 0,87 |
Temperaturas extremadamente bajas |
0,57 |
2.- Potencia necesaria para elevar la carga hasta una cierta altura (P2):
La segunda potencia parcial que es preciso conocer es la necesaria para elevar la carga que transporte la cinta hasta una cierta altura, o en caso descendente, la potencia necesaria para frenar la banda, es decir, es la potencia derivada de la inclinación que tenga la cinta.
P2 = |
H · Qm |
367 |
donde,
H : es la altura que alcanza la banda transportadora (m)
Qm : es la capacidad de transporte en masa de la banda (t/h)
La altura (H) que alcanza el extremo de la cinta se calcula a partir de la longitud (L) de la cinta y su inclinación (φ) mediante la expresión siguiente:
H = L · sen(φ)
3.- Potencia necesaria para vencer rozamientos de elementos auxiliares, dispositivos de limpieza y guías (P3):
La tercera potencia parcial que hay que calcular es la necesaria para vencer rozamientos de los elementos auxiliares que incorpore la cinta, como trippers, dispositivos de limpieza y guías.
En este caso, sólo habrá que calcular y sumar las potencias consumidas por cada uno de los elementos instalados:
P3 = Pa + Pb + Pc ...
donde,
Pa : es la potencia debida a los trippers (kW)
Pb : es la potencia debida a los dispositivos de limpieza (kW)
Pc : es la potencia debida a las guías y faldones instalados (kW)
A continuación, se incluye una tabla donde se estima la potencia consumida por cada una de los elementos auxiliares que se acople a la cinta transportadora, en función de la velocidad y anchura de la cinta:
Tabla 10. Potencias adicionales de equipos auxiliares |
||
|
Ancho de banda (m) |
Potencia (kW) |
Trippers, Pa |
≤ 500 |
0,8 · v |
≤ 1000 |
1,5 · v |
|
> 1000 |
2,3 · v |
|
Dispositivos de limpieza, Pb |
Tipo de contacto / presión |
|
Contacto simple |
0,3 · B · v |
|
Contacto elevado |
1,5 · B · v |
|
Guías de carga, Pc |
Longitud Lf (m) |
|
Desde punto de carga |
0,16 · v · Lf |
|
donde,
B : es el ancho de banda de la cinta (m)
v : es la velocidad de avance de la banda (m/s)
Lf : es la longitud de la guía o faldones (m)
La potencia total (PT) necesaria para el accionamiento de la cinta será igual a la suma de las anteriores potencias parciales:
PT = P1 + P2 +P3
Esta potencia (PT) es la que debe proporcionar el tambor motriz a la cinta. No obstante, esta potencia no es la definitiva.
En efecto, generalmente el tambor motriz de una cinta es accionado por un motorreductor eléctrico que engrana con el eje del tambor. Dicho motorreductor consta de un motor eléctrico más un reductor de velocidades que acople el eje de salida del motor eléctrico al el eje de entrada del tambor motriz.
Por tanto, habrá que tener en cuenta los rendimientos tanto del motor eléctrico como del reductor de velocidades que se utilice, que hace que se tenga que incrementar la potencia final necesaria.
De esta manera, la potencia requerida por el motor (PM) para el accionamiento del tambor motriz de la cinta será la obtenida de la siguiente expresión que tenga en cuenta los anteriores rendimientos:
PM = |
PT |
η |
donde,
PM : es la potencia consumida por el motor eléctrico (kW)
η : es el rendimiento total que tiene en cuenta tanto el rendimiento del motor como de la caja reductora.
Para el cálculo del rendimiento total (η), éste se realiza a partir de los rendimientos del motor eléctrico y de la caja reductora, mediante la siguiente expresión:
η = ηm · ηr
donde,
ηm : es el rendimiento del motor eléctrico
ηr : es el rendimiento de la caja reductora
Como valores de referencia se tiene que el rendimiento de un motor eléctrico convencional (ηm) se puede estimar entorno al 85-95%, mientras que si se trata del rendimiento de una caja de reductora (ηr), si ésta es de engranajes cilíndricos de dientes rectos y de varias etapas, el rendimiento en cada etapa de transmisión va a estar comprendido en el rango del 96 al 99%.
Una vez obtenida la potencia motora (PM) necesaria, se selecciona la potencia nominal del motor eléctrico que mejor se adapte a la instalación.
En la siguiente tabla se muestra las potencias nominales en kW de los motores eléctricos de mayor uso comercial para cintas transportadoras:
Tabla 11. Valores de las potencias normalizadas de motores eléctricos (kW) |
|||||||||
1,5 |
2,2 |
3 |
4 |
5,5 |
7,5 |
11 |
15 |
18,5 |
22 |
4.5- Resistencia mínima a tracción de la banda
Calculada la potencia (PT) de accionamiento que transmite el tambor motriz a la banda, es necesario saber cuál es la resistencia mínima que deberá tener la banda para evitar que se produzca su rotura. Esta resistencia será, como mínimo, igual a la fuerza de tracción máxima que el tambor motriz origine en la banda.
Para calcular el esfuerzo máximo de tracción que se origina en la banda, se suelen utilizar fórmulas experimentales que proporcionan los distintos fabricantes de bandas transportadoras.
En este tutorial, se va a emplear la siguiente expresión del fabricante Forbo Movement Systems que permite obtener el esfuerzo máximo de tracción que se origina en una banda transportadora, conocida su velocidad de avance y la potencia que transmite el tambor a la banda:
Fb = |
PT · C1 · 1000 |
v |
donde,
Fb : es la fuerza de tracción máxima de la banda (N)
PT : es la potencia de accionamiento que el tambor motriz transmite a la banda (kW)
v : es la velocidad de avance de la banda (m/s)
C1 : es un factor de servicio dado en tablas (-)
El factor C1 es un parámetro experimental que se obtiene de la siguiente tabla suministrada por el fabricante de la banda, en función del tipo de recubrimiento de la cara inferior de la banda, del ángulo de contacto entre banda y tambor motriz, y de las condiciones de la superficie del tambor motriz:
Tabla 12. Factor de Servicio, C1 |
||||||
Recubrimiento de la cara inferior de la banda |
V3, V5, U2, A5, E3 |
V1, U1, UH, U2H, V2H, V5H |
||||
Ángulo de contacto, α (en grados) |
180º |
210º |
240º |
180º |
210º |
240º |
|
|
|
|
|
|
|
Tambor de acero liso |
|
|
|
|
|
|
Seco |
1,5 |
1,4 |
1,3 |
1,8 |
1,6 |
1,5 |
Mojado |
3,7 |
3,2 |
2,9 |
5,0 |
4,0 |
3,0 |
|
|
|
|
|
|
|
Tambor con forro de fricción |
|
|
|
|
|
|
Seco |
1,4 |
1,3 |
1,2 |
1,6 |
1,5 |
1,4 |
Mojado |
1,8 |
1,6 |
1,5 |
3,7 |
3,2 |
2,9 |
|
||||||
Recubrimiento de la cara inferior de la banda |
0, U0, NOVO, E0, A0, T, P |
TX0 (AmpMiser) |
||||
Ángulo de contacto, α (en grados) |
180º |
210º |
240º |
180º |
210º |
240º |
|
|
|
|
|
|
|
Tambor de acero liso |
|
|
|
|
|
|
Seco |
2,1 |
1,9 |
1,7 |
2,9 |
2,6 |
2,3 |
Mojado |
No Recomendable |
No Recomendable |
||||
|
|
|
|
|
|
|
Tambor con forro de fricción |
|
|
|
|
|
|
Seco |
1,5 |
1,4 |
1,3 |
1,8 |
1,6 |
1,5 |
Mojado |
2,1 |
1,9 |
1,7 |
No Recomendable |
||
Una vez determinado el valor Fb del esfuerzo de tracción máxima a la que estará sometida la banda, se determina el valor de resistencia nominal mínima que deberá tener la banda.
Para el cálculo de la resistencia nominal mínima de la banda se puede emplear la siguiente expresión:
R = |
Fb · CS |
B |
donde,
R : es la resistencia nominal de la banda (N/mm)
Fb : es la fuerza de tracción máxima de la banda (N)
B : es el ancho de banda (mm)
CS : es un coeficiente de seguridad, según el tipo de banda:
CS = 8 para bandas con cable de acero
CS = 10 para el resto de bandas
Una vez determinado el valor R de la resistencia a tracción mínima de la banda, se deberá elegir una banda con un valor de resistencia nominal superior al calculado de entre los valores de resistencias normalizados por el fabricante.
Para la selección final de la resistencia nominal de la banda, se suelen utilizar tablas proporcionadas por los propios fabricantes de bandas transportadoras donde se incluyen los valores normalizados de las resistencias de las bandas textiles que se fabrican, como la tabla que se muestra a continuación:
Tabla 13. Resistencias nominales (RN) de las bandas textiles (N/mm) |
|||||||||
126 |
160 |
200 |
250 |
315 |
400 |
500 |
630 |
800 |
1000 |
NOTA: Se deberá seleccionar una banda con una Resistencia Nominal (RN) superior a la resistencia R calculada.
4.6- Cálculo de las tensiones de trabajo de la banda
La fuerza de arrastre del tambor motriz origina una serie de tensiones en los ramales de la banda debida a la tracción que ejerce la superficie del tambor motriz en su contacto con la cara interior de la banda.
Este nivel de tensiones no es uniforme en toda la longitud de la banda, sino que un ramal de la banda se encontrará sometido a más tensión que el otro ramal situado al otro lado del tambor motriz. La relación entre ambas tensiones de cada ramal de la banda se define mediante la ecuación de Euler-Eytelwein:
|
T1 |
= e μ·α |
| T2 |
donde,
T1 : es la tensión del lado más tenso de la banda (N)
T2 : es la tensión del lado menos tenso de la banda (N)
μ : es el coeficiente de fricción entre banda y tambor (-)
α : es el ángulo de contacto entre banda y tambor (rad)
En la siguiente tabla se incluyen los valores típicos del coeficiente de fricción (μ) entre banda y superficie del tambor, según las condiciones de servicio en los que trabaje la cinta:
Tabla 14. Valores del coeficiente de fricción, μ |
||
Superficie del Tambor |
Sin Recubrimiento |
Con Recubrimiento |
Alta adherencia |
0,35 |
0,45 |
Seca |
0,35 |
0,40 |
Húmeda |
0,20 |
0,35 |
Mojada |
0,10 |
0,30 |
Es importante resaltar que en una banda, uno de los ramales estará sometido a más tensión que el otro situado al otro lado del tambor, de manera que existirá un ramal tenso y otro ramal flojo.
Además, siempre será necesario que exista una cierta tensión en el lado flojo de la banda, de manera que si la tensión en el ramal suelto de la banda es demasiado pequeña o inexistente, la banda no avanzará correctamente, aunque gire el tambor motriz, dado que se producirá el resbalamiento de la banda sobre la superficie del tambor.
Por tanto, siempre será necesario que se mantenga una cierta tensión en el lado menos tenso de la cinta de manera que las dos tensiones (T1 y T2) cumplan siempre la ecuación de Euler-Eytelwein. De ahí que se empleen sistemas de contrapesos u otros mecanismos que sirvan para aplicar y mantener el ramal flojo tensado con una cierta tensión mínima.
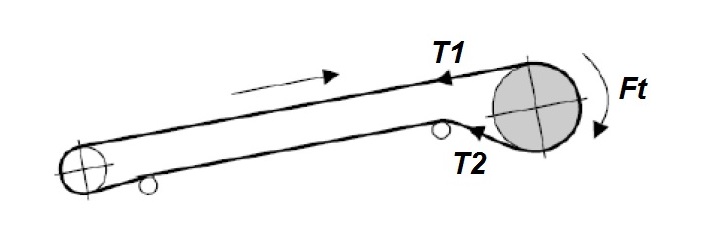
En la figura anterior se muestra el esquema de montaje que más se utiliza en una cinta transportadora, ya sean horizontales o inclinadas, donde el tambor motriz se sitúa en la cabeza de la instalación. Existen otros tipos de configuraciones posibles, por ejemplo, con el tambor motriz situado en cola de la cinta, o un tambor motriz en cola y otro en cabeza, o también se puede montar un sistema con dos tambores motrices en cabeza de la cinta.
La fuerza (Ft) tangencial que transmite el tambor motriz a la banda se produce por la diferencia entre las tensiones de entrada y salida de la banda a un lado y otro del tambor motriz que, como se ha visto en la ecuación de Euler-Eytelwein, ambas tensiones dependen del coeficiente de rozamiento entre la banda y el tambor.
Por tanto, y esto es lo más importante, para que se produzca movimiento en la banda es necesario que exista una tensión (T2) en el lado flojo. La diferencia entre las tensiones en el lado flojo y el lado tenso de la banda es la fuerza tangencial (Ft).
T1 = Ft +T2
donde,
T1 : es la tensión del lado más tenso de la banda (N)
T2 : es la tensión del lado menos tenso de la banda (N)
Ft : es la fuerza tangencial en el régimen de giro estacionario (N)
Para calcular la fuerza tangencial (Ft) que transmite el tambor motriz a la banda en estado estacionario, es decir, cuando la cinta está funcionando a régimen constante, se emplea la siguiente fórmula que calcula la potencia (PT) transmitida por el tambor motriz:
PT = |
Ft · v |
1000 |
donde,
Ft : es la fuerza tangencial en el régimen de giro estacionario (N)
v : es la velocidad de avance de la banda (m/s)
PT : es la potencia total transmitida por el tambor motriz (kW)
Y despejando la fuerza tangencial Ft de la anterior expresión, se tiene que:
Ft = |
PT · 1000 |
v |
Si el ramal flojo de la banda no tiene una tensión mínima, entonces la cinta no avanzará correctamente y la banda resbalará sobre la superficie del tambor motriz. El límite de la transmisión de potencia, antes de que se produzca el deslizamiento de la cinta sobre el tambor, viene dada por la expresión siguiente:
|
T1 |
< e μ·α |
| T2 |
donde,
T1 : es la tensión del lado más tenso de la banda (N)
T2 : es la tensión del lado menos tenso de la banda (N)
μ : es el coeficiente de fricción entre banda y tambor (-)
α : es el ángulo de contacto entre banda y tambor (rad)
Las expresiones anteriores sirven para calcular las tensiones de la banda cuando la cinta trabaja en el régimen estacionario, es decir, cuando la cinta ya ha alcanzado un régimen de velocidad constante.
Sin embargo, durante el tiempo que dura el arranque del motor, los niveles de tensiones que se alcanzan son sensiblemente superiores a los valores cuando la cinta ya funciona en régimen estacionario, por lo que es conveniente conocer estos niveles máximos de tensiones para evitar que se produzcan daños en la banda.
En general, se considera que el arranque de cualquier máquina es el periodo que transcurre por el cual se pasa de un estado de reposo inicial a un estado final estacionario con una velocidad de funcionamiento constante.
En el momento del arranque de la banda, es necesario aplicar un incremento de fuerza adicional respecto al estado estacionario para así poder acelerar desde su estado inicial en reposo a todas las masas que constituyen el sistema de la cinta, esto es, la masa del material a transportar, la banda, los rodillos, los tambores y demás elementos auxiliares. Esta aceleración que se le aplica al sistema deberá ser suficiente para vencer el par resistente inicial, pero debe mantenerse por debajo de un cierto valor para evitar que patine la banda.
Como buena práctica se considera que esta fuerza tangencial máxima en el arranque no deberá ser mayor de 1,6 veces el valor de la fuerza tangencial alcanzada en el estado estacionario.
Por lo tanto, se puede obtener la fuerza tangencial en el arranque (FtA) incrementando el valor de la fuerza tangencial del régimen estacionario, según la siguiente expresión:
FtA = 1,6 · Ft
Esta fuerza tangencial máxima no estacionaria (FtA) será aplicada sólo durante un determinado periodo de tiempo, justo lo que dure el periodo de arranque del motor de la cinta.
Para el cálculo de las tensiones T1 y T2 en los periodos de arranque del motor, se debe estimar un valor mayor del coeficiente de fricción (μA) que evite el deslizamiento de la banda sobre el tambor en los primeros momentos de arranque del motor, ya que en el arranque las tensiones que se transmiten se incrementan. Este incremento del coeficiente de fricción se puede estimar como:
μA = μ + 0,05
Teniendo en cuenta este coeficiente de fricción mayorado, las nuevas tensiones T1A y T2A en los ramales de la cinta durante el periodo de arranque del motor resultan ser:
T1A = |
FtA · e μA·α |
e μA·α - 1 |
T2A = |
FtA |
e μA·α - 1 |
4.7- Cálculo del diámetro y velocidad de giro del tambor motriz
Previo al cálculo de las cargas que actúan sobre el tambor motriz, es necesario conocer cuáles son los valores del diámetro y velocidad de giro del tambor motriz.
- Diámetro del tambor motriz (DT):
La norma DIN-22101 establece la siguiente expresión para calcular el diámetro mínimo del tambor motriz de accionamiento para bandas transportadoras:
DTmín = |
36 · Ft |
p · π · αº · B |
donde,
Ft : es la fuerza tangencial en el régimen de giro estacionario (N)
αº : es el ángulo de contacto entre banda y tambor (expresado en grados, º)
B : es el ancho de banda de la cinta (m)
p : es la capacidad de transmisión tambor/banda. Este parámetro suele estar comprendido entre 1600 - 2000 kg/m2
De la siguiente tabla que se adjunta, se puede seleccionar el diámetro nominal normalizado del tambor motriz que mejor se aproxime al valor calculado:
Tabla 15. Diámetros de tambores normalizados según la norma DIN-22101 (mm) |
||
200 |
250 |
320 |
400 |
500 |
630 |
800 |
1000 |
1250 |
1400 |
1600 |
1800 |
2000 |
||
El porcentaje (KT) de utilización del tambor motriz deberá estar comprendido entre el 60-100%. Si resultase un valor inferior se deberá reducir el valor establecido. Para determinar el porcentaje de utilización (KT) del tambor motriz se deberá emplear la siguiente expresión:
KT = |
T · CS |
B · RN · 100 |
donde,
T : es la tensión máxima de trabajo de la banda (N)
RN : es la resistencia nominal a tracción de la banda (N/mm)
B : es el ancho de banda de la cinta (en mm)
CS : es un coeficiente de seguridad, según el tipo de banda:
CS = 8 para bandas con cable de acero
CS = 10 para el resto de bandas
- Velocidad de giro del tambor motriz (nT):
Para el cálculo de la velocidad a la que gira el tambor motriz se emplea la siguiente expresión:
nT = |
v · 60 |
π · DT |
donde,
nT : es la velocidad del tambor motriz (r.p.m.)
v : es la velocidad de la banda (m/s)
DT : es el diámetro elegido del tambor motriz (m)
4.8- Cálculo de cargas sobre el tambor motriz
- Carga del tambor motriz en el arranque (FtA):
Durante el arranque se producen las máximas exigencias de fuerza por parte del motor para lograr acelerar la cinta desde cero hasta la velocidad de régimen. Esta fuerza de arranque que actúa sobre el tambor motriz se puede calcular a partir de las tensiones de la banda durante el arranque:
FtA = T1A + T2A
donde,
FtA : es la fuerza tangencial del tambor motriz en el arranque (N)
T1A : es la tensión del lado tenso de la banda en el arranque (N)
T2A : es la tensión del lado menos tenso de la banda en el arranque (N)
- Par motor en el arranque (MA):
Por último, se calcula el par motor máximo que se debe aplicar en el tambor motriz para el arranque de la cinta. Este valor es necesario conocerlo para poder diseñar correctamente las prestaciones del motor que accione la cinta:
MA = |
FtA · DT |
2 |
donde,
MA : es el par motor máximo en el arranque de la cinta (N·m)
FtA : es la fuerza tangencial del tambor motriz en el arranque (N)
DT : es el diámetro seleccionado del tambor motriz (m)
4.9- Selección final de la resistencia nominal de la banda
Una vez determinado el valor T de la tensión máxima a la que estará sometida la banda, se deberá elegir una banda con un valor de resistencia superior de entre los valores de resistencias que estén normalizados por el fabricante, de manera que se cumpla con los requisitos de seguridad por resistencia de la banda.
La resistencia nominal de la banda deberá ser, al menos, superior a la que se calcule mediante la siguiente expresión:
R = |
T · CS |
B |
donde,
R : es la resistencia nominal mínima que debe ofrecer la banda (N/mm)
T : es la tensión de trabajo máximo calculada en la banda (N)
B : es el ancho de banda (en mm)
CS : es un coeficiente de seguridad, según el tipo de banda:
CS = 8 para bandas con cable de acero
CS = 10 para el resto de bandas
Una vez determinado el valor R de la resistencia a tracción mínima que deberá ofrecer la banda, se deberá elegir una banda con un valor de resistencia nominal superior de entre los valores de resistencias que estén normalizados por el fabricante.
Para la selección de la resistencia nominal de la banda, se suelen utilizar tablas proporcionadas por los propios fabricantes de bandas transportadoras donde se incluyen los valores normalizados de las resistencias de las bandas textiles que se fabrican, como la tabla que se muestra a continuación:
Tabla 13. Resistencias nominales (RN) de las bandas textiles (N/mm) |
|||||||||
126 |
160 |
200 |
250 |
315 |
400 |
500 |
630 |
800 |
1000 |
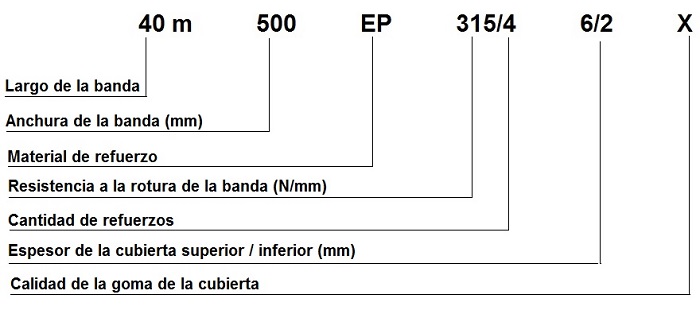
A continuación, se incluye el siguiente esquema donde se muestra, a modo de ejemplo, los datos que identifican a una banda transportadora y donde se detallan las principales características de la banda:
5- Ejemplo de cálculo de una cinta transportadora
En este apartado se mostrará cómo realizar los cálculos necesarios para el diseño de una cinta transportadora, siguiendo el procedimiento indicado en los apartados anteriores y haciendo uso de las correspondientes tablas incluidas en este tutorial:
1.- Datos iniciales de diseño:
• Material de transporte: trigo
• Longitud de la banda, L: 40 m
• Inclinación de la cinta, φ: 10º
• Altura alcanzada por la cinta, H: 7 m
• Ancho de banda, B: 500 mm
• Velocidad de avance de la cinta, v: 0,8 m/s
2.- Área (A) de la sección transversal del material transportado:
Según lo indicado en el apartado 4.2 se tiene que:
A = A1 + A2
donde,
A1 = 0,25 · tan(β) · [ l + (b - l) · cos(λ) ]2
A2 = l1 · sen(λ) · [ l + l1 · cos(λ) ]
siendo,
b = 0,9 · B - 0,05
l1 = 0,5 · (b - l)
Donde los datos iniciales que se tienen son:
β = 25º es el ángulo de sobrecarga del material transportado por la cinta (ver Tabla 6: Características de los materiales)
λ = 30º es el ángulo de artesa en que se disponen los rodillos en la cinta
l = 0,18 m es la longitud de los rodillos
B = 0,5 m es el ancho de banda de la cinta.
Con estos valores, se resuelven las anteriores expresiones:
b = 0,9 · B - 0,05 = 0,4
l1 = 0,5 · (b - l) = 0,11
A1 = 0,25 · tan(25º) · [ 0,18 + (0,4 - 0,l8) · cos(30º) ]2 = 0,016 m2
A2 = 0,11 · sen(30º) · [ 0,18 + 0,11 · cos(30º) ] = 0,015 m2
Luego, el área total de la sección transversal del material vale:
A = A1 + A2 = 0,016 + 0,015 = 0,031 m2
3.- Capacidad de transporte de la cinta:
Del apartado 4.3 se tiene que la capacidad de transporte volumétrica (Qv) de una cinta se calcula como:
Qv = 3600 · v · A · k
Donde los datos iniciales son:
v = 0,8 m/s es la velocidad de avance de la banda
A = 0,031 m2 es el área de la sección transversal del material transportado
k es un coeficiente de reducción de la capacidad de transporte por inclinación de la cinta. Este coeficiente se puede calcular aplicando la siguiente expresión:
k = 1 - 1,64 · ( |
φ · π |
)2 |
| 180 |
donde,
φ : es el ángulo de inclinación de la cinta ( φ = 10º )
Sustituyendo resulta:
k = 1 - 1,64 · ( |
10º · π |
)2 = 0,95 |
| 180 |
Por lo que la capacidad de transporte volumétrica (Qv) de la cinta vale:
Qv = 3600 · 0,8 · 0,031 · 0,95 = 84,82 m3/h
Para el cálculo de la capacidad de transporte en masa (Qm) es necesario conocer el peso específico (γ) del material transportado por la cinta.
Qm = Qv · γ = 84,82 · 0,75 = 63,62 t/h
donde,
γ = 0,75 t/m3 es el peso específico del material transportado, en este caso, trigo (ver Tabla 6. Características de los materiales)
4.- Potencia de accionamiento de la cinta:
Según el apartado 4.4 la potencia total (PT) será igual a la suma de las siguientes potencias parciales:
PT = P1 + P2 +P3
• Potencia necesaria para mover la cinta en vacío y cargada, con posición horizontal de la cinta (P1):
P1 = |
Cb · v + Qm |
Cl · Kf |
donde,
Cb = 67 (ver Tabla 7. Factor de ancho de la banda, Cb)
v = 0,8 m/s es la velocidad de avance de la banda
Qm = 63,62 t/h es la capacidad de transporte en masa de la banda
Cl = 192 (ver Tabla 8. Factor de longitud de la banda, Cl)
Kf = 1 (ver Tabla 9. Factor de servicio, Kf)
P1 = |
67 · 0,8 + 63,62 |
= 0,611 kW |
192 · 1 |
• Potencia necesaria para elevar la carga hasta una cierta altura (P2):
P2 = |
H · Qm |
367 |
donde,
H = 7 m es la altura que alcanza la cabeza de la banda transportadora
Qm = 63,62 t/h es la capacidad de transporte en masa de la banda
P2 = |
7 · 63,62 |
= 1,213 kW |
367 |
• Potencia necesaria para vencer rozamientos de elementos auxiliares, dispositivos de limpieza y guías (P3):
En este caso, sólo habrá que calcular y sumar las potencias consumidas por cada uno de los elementos instalados:
P3 = Pa + Pb + Pc ...
donde,
Pa : es la potencia debida a los trippers instalados (kW)
Pb : es la potencia debida a los dispositivos de limpieza (kW)
Pc : es la potencia debida a las guías y faldones instalados (kW)
Para la estimación del consumo de potencia debida a los elementos auxiliares se hace uso de la Tabla 10. Potencias adicionales de equipos auxiliares:
Pa = 0 dado que no hay trippers instalados
Pb = 0,3 · B · v = 0,3 · 0,5 · 0,8 = 0,12 kW
Pc = 0,16 · v · Lf = 0,16 · 0,8 · 3,75 = 0,48 kW
Siendo Lf = 3,75 m la longitud de los faldones instalados.
Luego la potencia consumida por los elementos auxiliares resulta ser:
P3 = 0,12 + 0,48 = 0,6 kW
La potencia total (PT) a transmitir por el tambor motriz para el accionamiento de la cinta será la suma de las anteriores potencias parciales:
PT = P1 + P2 +P3 = 0,611 + 1,213 + 0,6 = 2,424 kW
La potencia requerida por el motor (PM) para el accionamiento del tambor motriz de la cinta se calcula como:
PM = |
PT |
η |
donde,
η = ηm · ηr
siendo,
ηm = 0,91 es el rendimiento del motor eléctrico
ηr = 0,96 es el rendimiento de la caja reductora
Por lo tanto, el rendimiento total del motorreductor vale η = 0,91 · 0,96 = 0,87. Y la potencia consumida por el motor:
PM = |
2,424 |
= 2,786 kW |
0,87 |
De la Tabla 11. Valores de las potencias normalizadas de motores eléctricos, se selecciona un motor eléctrico con potencia nominal de 4 kW.
5.- Resistencia mínima a tracción de la banda (R):
En primer lugar se calcula el esfuerzo máximo de tracción (Fb) que se origina en la banda que, según el apartado 4.5, se puede calcular mediante la siguiente expresión:
Fb = |
PT · C1 · 1000 |
v |
Donde se tiene que,
PT = 2,424 kW es la potencia de accionamiento que el tambor motriz transmite a la banda
v = 0,8 m/s es la velocidad de avance de la banda
C1 = 1,4 (ver Tabla 12. Factor de Servicio, C1)
Por lo que se obtiene el siguiente valor:
Fb = |
2,424 · 1,4 · 1000 |
= 4242 N |
0,8 |
Una vez determinado el valor Fb del esfuerzo de tracción máxima a la que estará sometida la banda, el cálculo de la resistencia nominal mínima (R) de la banda se realiza empleando la siguiente expresión:
R = |
Fb · CS |
B |
donde,
R : es la resistencia nominal de la banda (N/mm)
Fb = 4242 N es la fuerza de tracción máxima de la banda
B = 500 mm es el ancho de banda de la cinta
CS = 10 es un coeficiente de seguridad, según el tipo de banda elegido.
Por lo que resulta un valor para la resistencia nominal mínima de:
R = |
4242 · 10 |
= 84,8 N/mm |
500 |
De la Tabla 13. Resistencias nominales de las bandas textiles, incluida en el apartado 4.5 de este tutorial, se selecciona una banda con resistencia nominal de valor 200 N/mm.
Con la elección de esta resistencia nominal para la banda, también se puede calcular el coeficiente de seguridad por resistencia a la tracción con la que trabajará la banda:
Cseg = |
200 |
= 2,4 |
84,8 |
6.- Cálculo de las tensiones de trabajo de la banda (T1 y T2):
• Estado estacionario
La fuerza tangencial (Ft) que transmite el tambor motriz a la banda en estado estacionario se calcula empleando la siguiente expresión ya vista en el apartado 4.6:
Ft = |
PT · 1000 |
v |
Donde se sabe que,
PT = 2,424 kW
v = 0,8 m/s
Y sustituyendo resulta una fuerza tangencial de valor:
Ft = |
2,424 · 1000 |
= 3030 N |
0,8 |
Una vez conocido el valor de la fuerza tangencial (Ft), ya se pueden calcular las tensiones en cada ramal de la banda, a un lado y otro del tambor motriz.
La ecuación de Euler-Eytelwein establece la relación entre ambas tensiones de cada ramal de la banda:
|
T1 |
= e μ·α |
| T2 |
donde,
T1 : es la tensión del lado más tenso de la banda (N)
T2 : es la tensión del lado menos tenso de la banda (N)
μ = 0,4 (ver la Tabla 14. Valores del coeficiente de fricción entre banda y superficie del tambor)
α = π radianes, es el ángulo de contacto entre banda y tambor motriz.
Y por otro lado se tiene que la diferencia entre las tensiones en el lado flojo y el lado tenso de la banda es precisamente la fuerza tangencial (Ft):
T1 = Ft + T2
Por tanto, sustituyendo los valores de los parámetros conocidos, el sistema de ecuaciones que se establece es el siguiente:
|
T1 |
= e 0,4·π |
| T2 |
T1 = 3030 + T2
Resolviendo el sistema de ecuaciones anterior, se obtienen los siguientes valores de tensiones en cada ramal de la banda:
T1 = 4235 N
T2 = 1205 N
• Estado NO Estacionario
Como se ha dicho anteriormente, durante el arranque se producen picos de tensiones que deben calcularse para poder comprobar la resistencia de la banda.
La expresión para el cálculo de la fuerza tangencial en el arranque (FtA) es:
FtA = 1,6 · Ft
Siendo Ft la fuerza tangencial que transmite el tambor motriz a la banda en estado estacionario, cuyo valor ya ha sido calculado anteriormente: Ft = 3030 N
Por lo tanto la fuerza tangencial en el arranque vale:
FtA = 1,6 · 3030 = 4848 N
Por otro lado, el coeficiente de fricción (μA) en los primeros momentos de arranque del motor se puede estimar como:
μA = μ + 0,05 = 0,4 + 0,05 = 0,45
Teniendo en cuenta este coeficiente de fricción mayorado, las nuevas tensiones T1A y T2A en los ramales de la cinta durante el periodo de arranque del motor resultan ser:
T1A = |
FtA · e μA·α |
e μA·α - 1 |
T2A = |
FtA |
e μA·α - 1 |
Que sustituyendo valores, resultan unas tensiones durante el arranque en cada ramal de la banda de valor:
T1A = 6406 N
T2A = 1558 N
7.- Cálculo del diámetro y velocidad de giro del tambor motriz:
• Diámetro del tambor motriz (DT)
DTmín = |
36 · Ft |
p · π · αº · B |
donde,
Ft = 3030 N es la fuerza tangencial en el régimen de giro estacionario
αº = 180º es el ángulo de contacto entre banda y tambor
B = 0,5 m es el ancho de banda de la cinta
p = 1800 kg/m2 es la capacidad de transmisión tambor/banda.
Sustituyendo se obtiene un valor mínimo para el diámetro del tambor de:
DTmín = |
36 · 3030 |
= 0,214 m = 214 mm |
1800 · π · 180º · 0,5 |
De la Tabla 15. Diámetros de tambores normalizados según la norma DIN-22101, se selecciona un diámetro normalizado para el tambor motriz de valor:
DT = 250 mm.
• Velocidad de giro del tambor motriz (nT)
nT = |
v · 60 |
π · DT |
donde,
v = 0,8 m/s es la velocidad de avance de la banda
DT = 0,250 m es el diámetro elegido del tambor motriz
Y sustituyendo valores resulta una velocidad de giro del tambor motriz de:
nT = |
0,8 · 60 |
= 61,1 r.p.pm. |
π · 0,250 |
8.- Cargas actuantes sobre el tambor motriz:
• Esfuerzo del tambor motriz en el arranque (FtA)
FtA = T1A + T2A
donde,
T1A : es la tensión del lado tenso de la banda en el arranque (N)
T2A : es la tensión del lado menos tenso de la banda en el arranque (N)
Sustituyendo los valores calculados anteriormente resulta:
FtA = T1A + T2A = 6406 + 1558 = 7964 N
• Par motor en el arranque (MA)
MA = |
FtA · DT |
2 |
donde,
FtA = 7964 N es la fuerza tangencial del tambor motriz en el arranque
DT = 0,250 m es el diámetro seleccionado del tambor motriz
Resulta un par de arranque de:
MA = 995,5 N·m
9.- Selección final de la resistencia nominal de la banda:
La resistencia nominal de la banda deberá ser, al menos, superior a la que se calcule mediante la siguiente expresión:
R = |
T · CS |
B |
donde,
R : es la resistencia nominal mínima que debe ofrecer la banda (N/mm)
T : es la tensión de trabajo máximo calculada en la banda (N)
B : es el ancho de banda (en mm)
CS : es un coeficiente de seguridad, según el tipo de banda:
CS = 8 para bandas con cable de acero
CS = 10 para el resto de bandas
La tensión T máxima calculada en todo el proceso es T = 6406 N, que se corresponde con la tensión del ramal más tenso durante el arranque. Sustituyendo valores resulta:
R = |
6406 · 10 |
= 128,1 N/mm |
500 |
De la Tabla 13. Resistencias nominales de bandas textiles se selecciona una con resistencia nominal de 200 N/mm.
Con esta elección se obtiene un coeficiente final de seguridad en la banda por resistencia a la tracción de:
Cseg = |
200 |
= 1,56 |
128,1 |
ANEXOS
›› Anexo nº 1.- Guía de ingeniería y diseño de cintas transportadoras
›› Anexo nº 2.- Catálogo técnico de componentes para cintas transportadoras
Programa de Colaboración
Ahora puedes colaborar en el sostenimiento de esta web realizando un pequeño donativo
Gracias por tu colaboración
Hermenegildo Rodríguez Galbarro
Editor y Responsable de esta Web. [+info]
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055
