- Tutorial nº 14 -

Distribución de Esfuerzos
sobre el Bastidor del Vehículo

Índice de contenidos:

1- Caso A: Camión con Caja de Carga Ordinaria

1.1- Modelo de cálculo del vehículo

1.2- Características del bastidor del vehículo

1.3- Reparto de la carga por eje

1.4- Cálculo de los esfuerzos cortantes y momentos flectores

1.5- Comprobación por resistencia del bastidor del vehículo

2- Caso B: Camión con Caja Basculante

2.1- Modelo de cálculo del vehículo

2.2- Características del bastidor del vehículo

2.3- Reparto de la carga por eje

2.4- Cálculo de los esfuerzos cortantes y momentos flectores

2.5- Comprobación por resistencia del bastidor del vehículo

3- Caso C: Camión con Plataforma Elevadora de Carga Trasera

3.1- Modelo de cálculo del vehículo

3.2- Características del bastidor del vehículo

3.3- Reparto de la carga por eje

3.4- Cálculo de los esfuerzos cortantes y momentos flectores

3.5- Comprobación por resistencia del bastidor del vehículo

• ANEXOS:  Ejemplos de Proyectos de Reformas de Vehículos

››  Proyecto de Refoma en Vehículo Industrial para el Montaje de una Cisterna para el Transporte de Líquidos

››  Proyecto de Reforma en Vehículo para su Transformación en Vehículo Volquete

››  Proyecto de Reforma en Vehículo para el Montaje de una Plataforma Elevadora de Carga Trasera

---

DESARROLLO DEL CONTENIDO

---

1- Caso A: Camión con Caja de Carga Ordinaria

1.1- Modelo de cálculo del vehículo

Cuando se realiza una reforma de un vehículo, es necesario realizar una comprobación por resistencia del bastidor o estructura portante encargada de soportar, tanto la nueva carrocería montada, como la carga útil que transporte, con objeto de ver si es necesario reforzar la estructura que constituye el autobastidor del vehículo.

En general, cuando se realiza la instalación de una caja de carga en un camión, ésta se realiza sobre una nueva estructura portante o sobrebastidor auxiliar que se monta coincidente sobre los largueros del bastidor original o autobastidor del vehículo en toda su longitud. Con ello se consigue mejorar la resistencia del bastidor original del camión y conseguir también una mejor distribución de las cargas sobre el vehículo.

En este apartado se va a estudiar un primer caso, consistente en un camión al cual se le va a instalar una caja de carga fija al bastidor del vehículo, destinada al transporte normal de mercancías.

Para definir un modelo gráfico del problema, que facilite las labores de cálculo de la estructura portante del vehículo, se tendrá en cuenta los siguientes pesos por separados:

Q'   va a servir para designar el peso en autobastidor del vehículo, es decir, el peso del camión sin carrozar o en chasis-cabina, tal como sale de la planta de montaje.

Q₁   designará el peso del carrozado añadido al vehículo, es decir, el peso de la nueva caja de carga (que incluye el piso de la caja, portalones laterales, etc.), los largueros que conforman el sobrebastidor auxiliar, así como los elementos de anclaje de la caja al sobrebastidor auxiliar.

Q₂   será el peso máximo de mercancía que pueda transportar el vehículo en la caja de carga, es decir, será la carga útil.

Asimismo, se denomina TARA del vehículo a la que resulta de sumarle al peso en autobastidor o chasis cabina (Q'), el peso de la nueva carrocería montada o caja de carga (Q₁), incluyendo la dotación completa de combustible, lubricantes y herramientas del vehículo, es decir,

TARA = Q' + Q₁+ S

siendo "S" el peso de la dotación completa de combustible, lubricantes, fluidos hidráulicos, herramientas y ruedas de repuestos.

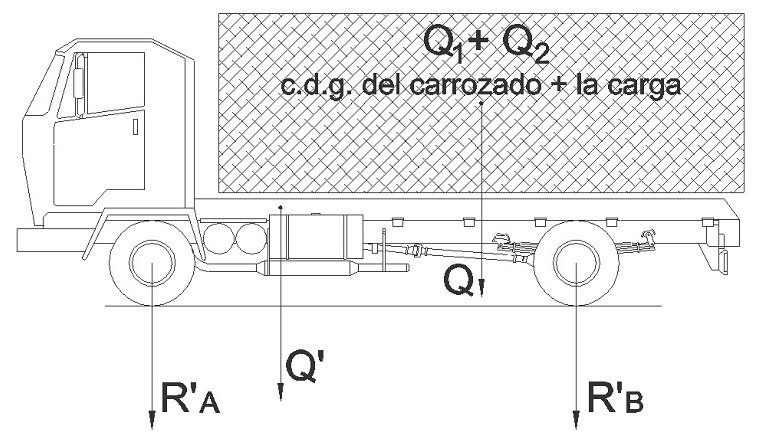
Si se denominan R'_A y R'_B los pesos que gravitan por separado sobre los ejes delantero y trasero respectivamente, debido al peso en autobastidor del vehículo, entonces se tendrá que: Q' = R'_A + R'_B

Y por otro lado, también se denominará Q = Q₁ + Q₂, siendo (Q) la suma del peso propio de la caja de carga (Q₁) más la mercancía o carga útil que pueda transportar (Q₂).

Como modelo de cálculo se va a emplear los datos de un camión de dos ejes con una masa máxima en carga admisible (MMA) total del vehículo prevista para su matriculación/circulación por vías públicas de 8.600 kg.

Esta masa máxima admisible (MMA) supone el vehículo totalmente cargado y que incluye, además del peso del vehículo con su carrocería y su carga, los pesos del conductor, pasajeros y dotación completa de combustibles, lubricantes, herramientas, etc. Representa el peso máximo que el vehículo reglamentariamente NO puede superar para poder circular, en ningún caso.

A continuación se adjunta la siguiente tabla resumen con las masas máximas autorizadas (total del vehículo y por ejes) que se va a seguir como modelo de cálculo en este tutorial.

Recordar, que las masas aquí incluidas no podrán ser superadas en ningún caso por el diseño propuesto del vehículo durante su uso normal:

 

Por último se incluirá otra tabla que recoge el peso en autobastidor del vehículo de referencia (Q'), tanto el total como lo que gravita por cada eje:

 

1.2- Características del bastidor del vehículo

Como se sabe, todo camión o vehículo industrial dispone de una estructura portante, llamado bastidor o autobastidor del vehículo, formada por dos largueros en acero, generalmente con perfil de sección en forma de  [ , que se encargan de recibir el peso de la carga y transmitirla a los ejes del vehículo.

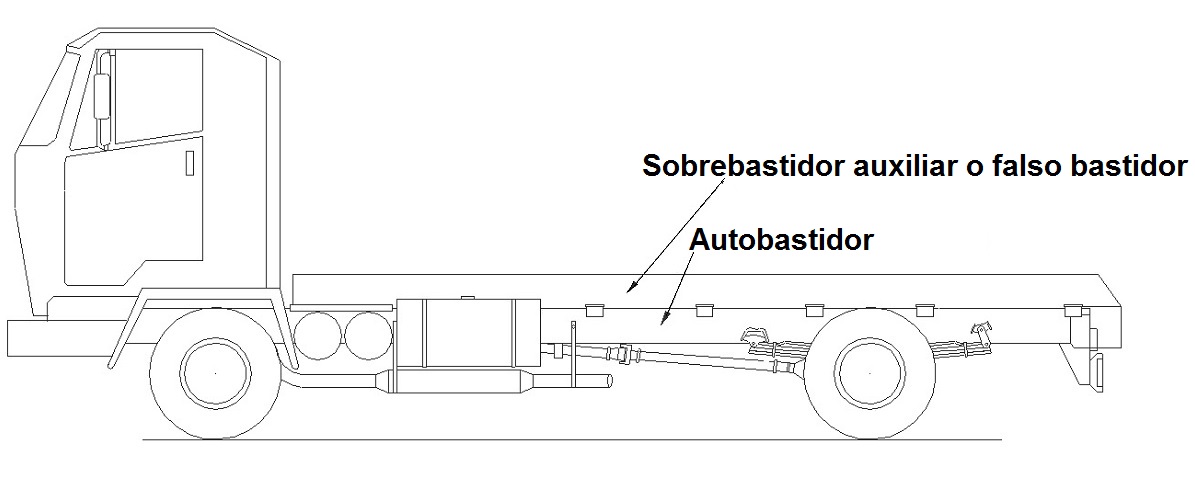
Sin embargo, antes de montar cualquier carrocería sobre el vehículo (una caja de carga, una plataforma portavehículos, una cisterna, etc.) conviene reforzar esta estructura original o autobastidor, que es la que trae de fábrica el vehículo, con otra estructura auxiliar portante, llamado también sobrebastidor auxiliar o falso bastidor, y que se monta sobre el bastidor original del vehículo.

Durante el montaje, los largueros del falso bastidor se ajustarán perfectamente sobre los perfiles del bastidor del vehículo en toda su longitud. Con ello se conseguirá una distribución y transmisión uniforme de las cargas desde la carrocería hacia el bastidor del vehículo, además de garantizar una correcta fijación y anclaje de la carrocería a la estructura portante del vehículo.

Como norma general, para la fabricación del sobrebastidor auxiliar, se deberán emplear materiales, en este caso acero, de características iguales ó superiores al tipo de acero empleado en la fabricación del bastidor del vehículo.

En los casos que se requieran esfuerzos más elevados, o cuando se desee evitar secciones de gran altura en el perfil del sobrebastidor, entonces sí será necesario utilizar materiales de características superiores a los empleados en el bastidor del vehículo.

En todo caso, se recomienda que el acero empleado para la elaboración del falso del bastidor tenga unas buenas propiedades para la soldadura.

Como norma general, la calidad del tipo de acero recomendado, para todos los casos, será como mínimo St-52-3:

 

A continuación se muestra en la siguiente figura, una sección transversal de los perfiles que conforman los largueros de la estructura del autobastidor y sobrebastidor del vehículo, que se ha tomado como modelo para el cálculo en este tutorial:

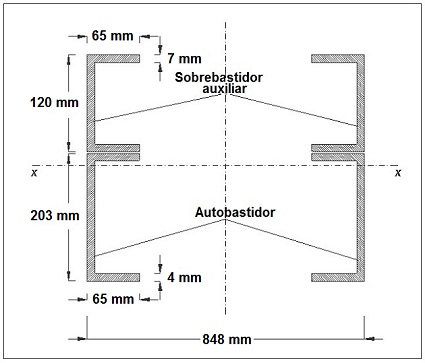
donde,

h₁ = 203 mm,  es la altura del alma del perfil que forma el autobastidor.

b₁ = 65 mm,  es la anchura del ala del perfil que forma el autobastidor.

e₁ = 4 mm,  es el espesor de pared del perfil que forma el autobastidor.

h₂ = 120 mm,  es la altura del alma del perfil que forma el sobrebastidor auxiliar.

b₂ = 65 mm,  es la anchura del ala del perfil que forma el sobrebastidor auxiliar.

e₂ = 7 mm,  es el espesor de pared del perfil que forma el sobrebastidor auxiliar.

 

Por otro lado, para la comprobación por resistencia de la sección de la estructura portante que conforman tanto el autobastidor y el sobrebastidor auxiliar, será necesario conocer su módulo resistente respecto al eje x-x neutro de la sección que es el eje de flexión del perfil, tal como se muestra en la figura anterior.

El módulo resistente a flexión de la sección total de uno de los largueros reforzados, es decir, el formado por autobastidor más el sobrebastidor auxiliar, viene dada por la siguiente expresión:

donde,

I_xx   es el momento de inercia del perfil de un larguero del bastidor reforzado respecto al eje x-x neutro de la sección.

y_máx   es la distancia del eje neutro de la sección a la fibra más alejada de la misma.

De acuerdo a las dimensiones mostrada en la figura anterior correspondiente a los perfiles de la estructura portante empleada en el vehículo, los valores de las propiedades mecánicas de estos perfiles son las siguientes:

• Módulo resistente a flexión del perfil de un larguero (autobastidor+sobrabastidor auxiliar) respecto al eje x-x neutro de la sección total reforzada, W_x = 155 cm³.

• Módulo resistente a flexión del perfil de un larguero del autobastidor sin refuerzo, con respecto a su eje neutro x₁-x₁, cuyo valor es de W_x1 = 77 cm³.

• Módulo resistente a flexión del perfil de un larguero del sobrebastidor auxiliar, con respecto a su eje neutro x₂-x₂, cuyo valor es de W_x2 = 64 cm³.

• Momento de inercia del perfil de un larguero del autobastidor sin refuerzo, I_x1 = 783 cm⁴.

• Momento de inercia del perfil de un larguero del sobrebastidor auxiliar, I_x2 = 382 cm⁴.

 

1.3- Reparto de la carga por eje

Previo a realizar el análisis de los esfuerzos que actúan sobre la estructura portante del vehículo, es necesario conocer cómo se distribuye el peso de la caja de carga más la carga útil transportada sobre cada eje del vehículo.

Como sabemos de apartados anteriores, con Q₁ se denominaba el peso de la carrocería formada por la caja de carga y Q₂ es el peso máximo de la mercancía que puede transportar el camión o carga útil.

Entonces, se llamará Q a la suma de ambos, es decir, al peso del carrozado de la caja de carga más la carga útil:

Q = Q₁ + Q₂

Según el tipo de vehículo tomado como modelo de cálculo para este tutorial, éste se trata de un vehículo de dos ejes, tipo 4x2 (con la tracción en el eje trasero).

 

Para vehículos 4x2 en posición de marcha y con carga uniformemente repartida sobre la caja de carga, el cálculo de las reacciones sobre los ejes del vehículo, delantero (R_A) y trasero (R_B), viene dado por las siguientes expresiones:

donde:

L   es la longitud de la caja de carga, en mm.

a   es el voladizo posterior de la caja de carga, en mm.

p   es la distancia entre ejes del vehículo, en mm.

m   es la distancia desde el eje delantero al comienzo de la caja de carga, en mm.

Q   es el valor del peso de la caja de carga más la carga útil que puede transportar, en kg. (Q = Q₁ + Q₂).

Las expresiones anteriores que proporcionan las reacciones sobre los ejes del vehículo, son el resultado de aplicar equilibrio de las fuerzas y momentos actuantes. En esta ocasión se está considerando que la mercancía o carga útil que transporta el vehículo se distribuye uniformemente a lo largo de la caja de carga, resultando así aplicada su resultante en el centro de gravedad (c.d.g.) de la caja de carga, que coincide con su centro geométrico, al considerarse también la caja de carga de características constructivas simétrica respecto a sus ejes medios.

En la siguiente tabla se incluyen las medidas geométricas del vehículo de referencia tomado como modelo de cálculo:

 

Por otro lado, la masa máxima en carga admisible prevista para matriculación/circulación (MMA) del vehículo de referencia para este tutorial, según está indicado en el apartado 1.1 anterior, es de 8.600 kg.

Asimismo, el peso del vehículo en chasis-cabina (Q') es de 3.185 kg, igualmente indicado en el apartado 1.1.

De la propia definición de la masa máxima admisible (MMA) del vehículo se tiene que,

MMA = Q' + Q₁ + Q₂ = Q' + Q

Como MMA = 8.600 kg  y  Q' = 3.185 kg, entonces se tiene que,

Q = MMA - Q' = 8600 - 3185 = 5.415 kg

Por tanto, aplicando los valores de las dimensiones del vehículo de la tabla 4 anterior y con el peso Q = 5.415 kg, las expresiones de cálculo de las reacciones en los ejes del vehículo quedan como sigue:

Resultando:

R_A = 841 kg

R_B = 4574 kg

Se incluye la siguiente tabla resumen con la distribución de cargas obtenida por cada eje, comprobándose que no se superan los límites establecidos, tanto por ejes como del total máximo permitido para el vehículo:

 

1.4- Cálculo de los esfuerzos cortantes y momentos flectores

El cálculo de la distribución de las leyes de esfuerzos cortantes y de momentos flectores a lo largo de la estructura portante que conforma el bastidor del vehículo se realiza estableciendo ecuaciones de equilibrio entre fuerzas (para el cálculo de los esfuerzos cortantes) y momentos (para el cálculo de la distribución de los momentos flectores).

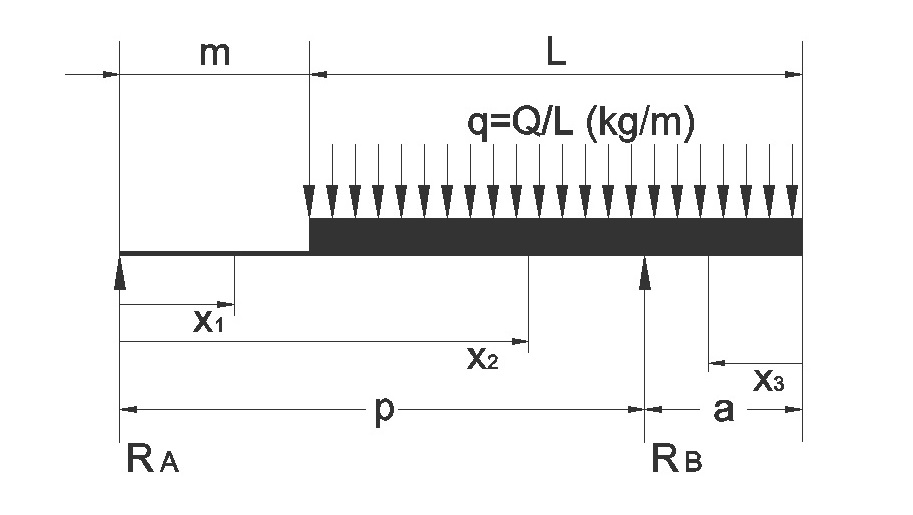
Según se representa en la figura adjunta, las fuerzas actuantes sobre el bastidor del vehículo son, por un lado, las reacciones que transmiten los ejes delantero (R_A) y trasero (R_B) del vehículo, y por otro lado, el peso propio de la caja de carga (Q₁) más el peso de la carga a transportar o carga útil (Q₂). Como ya se vio, su suma resulta la carga Q = Q₁ + Q₂

Asimismo, la carga Q (kg) se supone para el cálculo uniformemente distribuida a lo largo de la caja de carga, pudiéndose expresar como una carga lineal (q) que actúa en toda la longitud de la caja de carga de valor, q = Q/L (kg/m), siendo L la longitud de la caja de carga.

La forma de proceder para establecer las leyes de esfuerzos y momentos es muy sencilla: se irá recorriendo la longitud del bastidor del vehículo por tramos, estableciéndose el equilibrio de fuerzas y momentos en cada tramo.

Para este caso, los distintos tramos en que se dividirá la longitud del bastidor serán los siguientes:

• Tramo I:  para m ≥ x₁ > 0; siendo m = 0,535 m, la distancia desde el eje delantero al comienzo de la caja de carga, según se indicaba en la Tabla 4 "Dimensiones geométricas del vehículo carrozado". Por tanto, el Tramo I abarca desde la posición del eje delantero hasta el punto del bastidor donde comienza la caja de carga.

• Tramo II:  para p ≥ x₂ > m; siendo p = 4,185 m, la distancia entre los ejes delantero y trasero del vehículo, según se indicaba también en la Tabla 4. Este Tramo II abarca el tramo de bastidor desde el comienzo de la caja de carga hasta el punto del bastidor donde se sitúa el eje trasero del vehículo.

• Tramo III:  para a ≥ x₃ > 0; siendo a = 2,350 m, el voladizo posterior de la caja de carga, según se indicaba en la Tabla 4. El Tramo III abarca la parte final del bastidor desde el eje trasero del vehículo hasta el extremo posterior de la caja de carga.

A continuación se establecerán las ecuaciones de equilibrio, según los tramos en que queda dividido el bastidor del vehículo, para obtener las leyes de esfuerzos cortantes y de momentos flectores que actúan sobre el bastidor del vehículo:

• Tramo I:

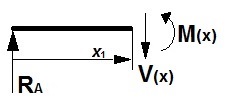
Para x₁=0:

V(0)= R_A= 841 kg

M(0)= 0;

Para m=0,535 m. ≥ x₁ > 0:

V(x₁)= R_A= 841 kg

M(x₁)= R_A·x₁= 841·x₁      (m·kg);

siendo  M_máx= 450 m·kg,  para x₁=0,535 m.

 

• Tramo II:

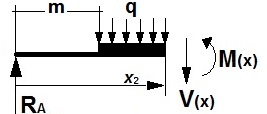
Para p=4,185 m ≥ x₂ > m=0,535 m:

V(x₂)= R_A-q·(x₂-m)= 841-902,5·(x₂-0,535);  de donde q= Q/L= 5415/6,0= 902,5 kg/m;

siendo  V_máx= -2453 kg,  para x₂= 4,185 m.

M(x₂)= R_A·x₂-q/2·(x₂-m)²= 841·x₂-451,25·(x₂-0,535)²      (m·kg)

siendo  M_máx= -2492 m·kg,  para x₂= 4,185 m.

 

• Tramo III:

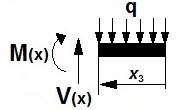
Para a=2,350 m ≥ x₃ > 0:

V(x₃)= q·x₃= 902,5·x₃      (Kg)

siendo  V_máx= -2121 kg,  para x₃=2,350 m.

M(x₃)= -q/2·(x₃)²= -451,25·(x₃)²      (m·kg)

siendo  M_máx= -2492 m·kg,  para x₃=2,350 m.

A continuación, se realiza una representación gráfica de las anteriores ecuaciones para visualizar mejor cómo es la distribución de los esfuerzos cortantes y de los momentos flectores sobre el bastidor del vehículo, con objeto de poder apreciar mejor el tramo de bastidor donde se alcanzan los valores máximos:

GRÁFICOS DE ESFUERZOS Y MOMENTOS

 

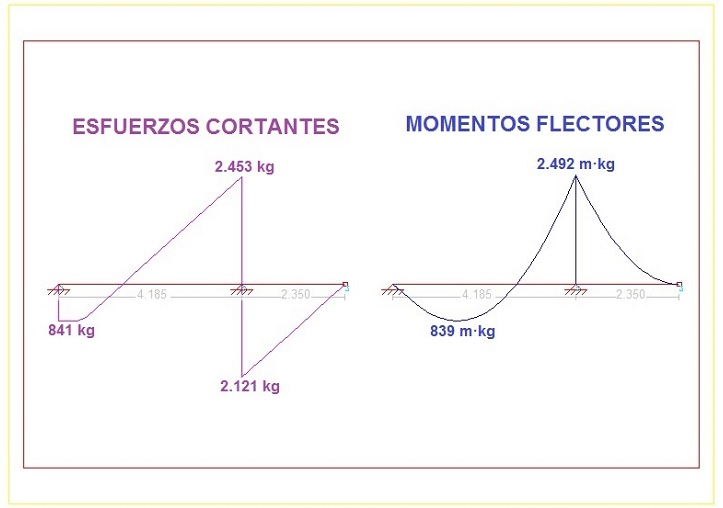
1.5- Comprobación por resistencia del bastidor del vehículo

Para la comprobación por resistencia del bastidor del vehículo se debe, en primer lugar, identificar el sitio del bastidor donde se alcancen los esfuerzos más desfavorables.

En este caso, y según se muestra en los gráficos de distribución de esfuerzos del apartado anterior, coincide en el lugar del bastidor donde el eje trasero está situado. En este punto y según el apartado 1.4 anterior, los valores de los esfuerzos obtenidos son los siguientes:

• Momento flector máximo, M = 2.492 m·kg

• Esfuerzo cortante máximo, V = 2.453 kg

 

Una vez identificado los esfuerzos máximos, se procede a calcular los valores de tensión (normal y de cortadura) que genera en la sección del bastidor estos esfuerzos:

-  Tensión normal a la sección debida al momento flector, o tensión de flexión (σ_f):

La tensión de trabajo a flexión que se produce en la sección del bastidor debida al momento flector (M) actuante viene dada por la siguiente expresión:

siendo,

M  el valor del momento flector que actúa en ese punto del bastidor, de valor M = 2.492 m·kg (249.200 cm·kg)

W_x  es el módulo resistente a flexión de la sección de un larguero del bastidor reforzado del vehículo, es decir, bastidor+sobrabastidor auxiliar, respecto al eje x-x neutro de la sección. Este valor, según se vio en el apartado 1.2 anterior para el bastidor empleado en el vehículo, es de W_x=155 cm³.

En la expresión anterior aparece en el denominador  2·W_x  debido a que el esfuerzo es resistido por los dos largueros que constituyen el bastidor del vehículo y sobre los que se apoya la caja de carga.

Sustituyendo valores se tiene que,

Resultando,

σ_f =  804 kg/cm²

 

-  Tensión de cortadura (τ):

Por otro lado, todo esfuerzo cortante (V_z) genera una tensión de cortadura o tensión tangencial (τ) en la sección del perfil, que en el caso de un perfil abierto de pared delgada, viene determinado por la siguiente expresión:

donde,

V_z  es el esfuerzo cortante que actúa en la sección del perfil

S_x  es el momento estático de media sección respecto al eje x de flexión

e  es el espesor de pared del perfil que constituye la sección del perfil

I_xx  es el momento de inercia de la sección del perfil respecto al eje x de flexión.

La tensión de cortadura será máxima en el eje x-x neutro de la sección, y nula en los extremos superior e inferior de la sección. En la siguiente figura se muestra el valor de las tensiones de cortadura máxima (τ_máx) para los tipos de secciones de bastidor más comúnmente empleadas en aplicaciones de reformas en vehículos. En todos los casos, el esfuerzo cortante (V_z) actúa siempre paralelo al eje z vertical y pasa por la línea que contiene al centro de esfuerzos cortantes de la sección.

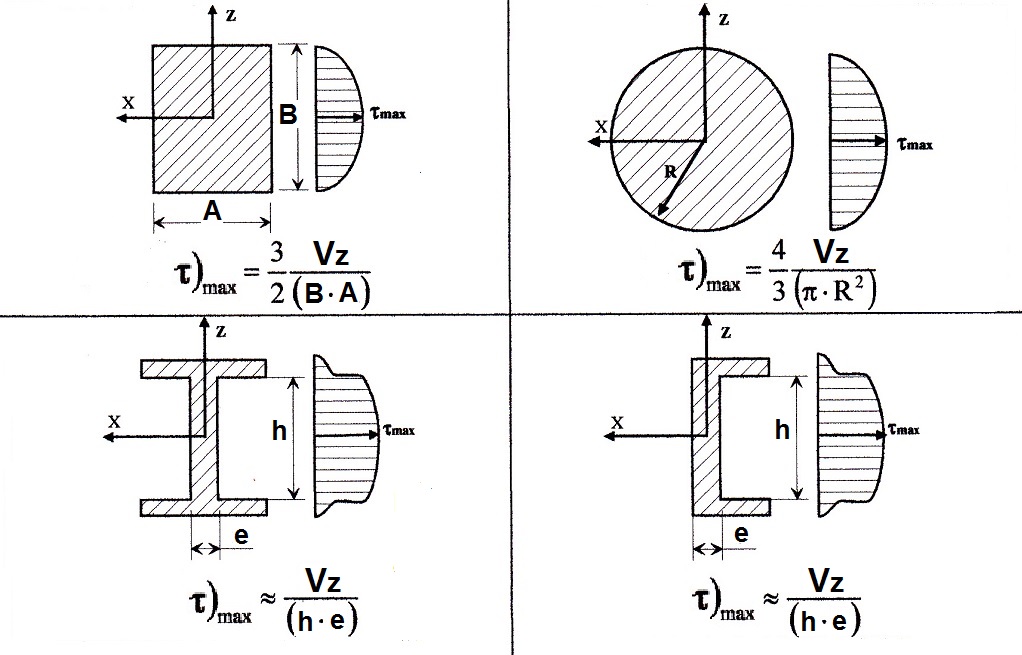
Como se ve en la figura anterior, en los perfiles estructurales abiertos de pared delgada, como es el tipo  [  empleado en el bastidor del vehículo, el esfuerzo cortante es absorbido casi en su totalidad por el alma que constituye la pared vertical del perfil, siendo prácticamente nula la aportación de las alas horizontales del perfil en resistir la acción del cortante.

Por lo tanto, y teniendo en cuenta además que el esfuerzo cortante (V) actuante tiene que ser absorbido por los dos largueros que conforman el bastidor del vehículo, la tensión de cortadura (τ) máxima que se genera en cada larguero del bastidor, se puede expresar como:

donde,

A_c  es la denominada área de cortadura de la sección del bastidor, que es la que absorbe todo el esfuerzo cortante.

Por tanto, para perfiles de pared delgada con secciones en  [ , el área de cortadura puede ser obtenida por la siguiente expresión: A_c = 2/3·h·e, siendo "e" el espesor de pared del perfil, y "h" es la altura del alma del perfil.

De manera que el valor de la tensión de cortadura máxima que se produce en la sección del bastidor se podrá calcular también como:

Como ya se indicó en el apartado 1.2, para reforzar el autobastidor original del vehículo, se ha superpuesto encima otro sobrebastidor auxiliar con objeto de mejorar la resistencia del conjunto, según se indicaba en la figura del apartado 1.2 anterior donde se muestra una sección transversal de los perfiles que conforman los largueros de la estructura del autobastidor y sobrebastidor del vehículo.

En este caso, la altura total del alma del bastidor reforzado será la suma de la altura del alma del bastidor original del vehículo más la del sobrebastidor auxiliar, es decir, h = h₁ + h₂, según la citada figura del apartado 1.2.

En definitiva, aplicando la expresión que proporciona la tensión máxima de cortadura (τ), resulta:

donde,

V  es el esfuerzo cortante que actúa sobre el bastidor en el punto más desfavorable, de valor V = 2.453 kg, según se vio al principio del apartado

h  es la altura total del alma del bastidor reforzado, de valor h = h₁+h₂ = 203+120 = 323 mm (32,3 cm)

e  es el espesor de pared del alma del bastidor, de valor e = 4 mm (0,4 cm)

Sustituyendo estos valores en la expresión anterior, se tiene que:

Resultando finalmente, una tensión de cortadura máxima de valor:

τ =  142 kg/cm²

Una vez calculados los valores de las tensiones normales debida a la flexión (σ_f) y tangenciales (τ) máximas, la tensión de comparación (σ_co), o tensión de Von Mises, viene dada por la conocida expresión siguiente:

σ_co = (σ_f² + 3· τ² )^1/2

que sustituyendo los valores obtenidos resulta una tensión de comparación de:

σ_co = (804² + 3· 142² )^1/2 =  841 kg/cm²

Tomando como referencia el límite elástico del material del que está fabricado el bastidor y refuerzo, se debe cumplir siempre que:

σ_co < σ_e

donde (σ_e) es el límite elástico del acero empleado para fabricar el bastidor del vehículo. Según el apartado 1.2 donde se describían las características y propiedades del bastidor del vehículo, el límite elástico del acero empleado es de,

σ_e = 36 kg/mm² = 3600 kg/cm²

Por lo que se cumple que,

σ_co = 841 kg/cm² < σ_e = 3600 kg/cm²

Por último, el coeficiente de seguridad obtenido para el trabajo conjunto del bastidor reforzado vendrá dado por:

λ = σ_e /σ_co = 3600/841 = 4,2 > 3

Se recomienda, como medida de seguridad estructural, que el coeficiente de seguridad que se obtenga para el bastidor reforzado del vehículo sea mayor a 3 (λ = σ_e /σ_co > 3), como efectivamente así se cumple en nuestro ejemplo.

2- Caso B: Camión con Caja Basculante

2.1- Modelo de cálculo del vehículo

En los vehículos con caja basculante, llamados también vehículos volquetes, la descarga de la mercancía se realiza por basculación de la caja de carga. Para ello, este tipo de vehículos necesitan de la instalación de un actuador o cilindro hidráulico acoplado al chasis del vehículo y a la caja basculante, el cual transmite un esfuerzo de empuje entre el chasis y la caja de carga que la hace girar alrededor del bulón de giro situado en el voladizo trasero del chasis del vehículo.

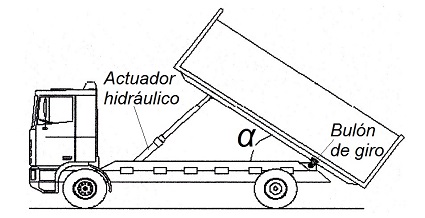
El propio trabajo de basculación de la caja de carga crea una distribución de esfuerzos distinta en el bastidor del vehículo a la que se obtenía en el caso anterior de este tutorial con una caja de carga ordinaria fija.

En efecto, durante el proceso de elevación de la caja de carga se crean dos nuevas cargas puntuales sobre el bastidor del vehículo. Una de ellas es el empuje del actuador hidráulico que actúa en el punto de anclaje con el chasis del vehículo, mientras que la otra carga puntual se sitúa en el punto de articulación de la caja de carga, es decir, donde bascula para voltear.

Igual que para el caso anterior, para definir un modelo gráfico del esquema de trabajo se tendrá en cuenta los siguientes pesos por separados:

Q'   va a servir para designar el peso en autobastidor del vehículo, es decir, el peso del camión sin carrozar o en chasis-cabina.

Q₁   designará el peso de la caja de carga, así como el peso de la instalación hidráulica (actuadores, bomba y depósito hidráulicos) y de los largueros y travesaños que conforman el sobrebastidor auxiliar de refuerzo al chasis.

Q₂   será el peso máximo de mercancía que pueda transportar el vehículo en la caja de carga, es decir, será la carga útil.

Asimismo, se denomina TARA del vehículo a la que resulta de sumarle al peso en autobastidor o chasis cabina (Q'), el peso de la nueva carrocería montada (Q₁), incluyendo la dotación completa de combustible, lubricantes y herramientas del vehículo, es decir,

TARA = Q' + Q₁ + S

siendo "S" el peso de la dotación completa de combustible, lubricantes, fluidos hidráulicos, herramientas y rueda de repuesto.

Si se denominan R'_A y R'_B los pesos que gravitan por separado sobre los ejes delantero y trasero respectivamente, debido al peso en autobastidor del vehículo, entonces se tendrá que: Q' = R'_A + R'_B

Y por otro lado, también se denominará Q = Q₁ + Q₂, siendo (Q) la suma del peso propio de la caja de carga (Q₁) más la mercancía o carga útil que pueda transportar (Q₂).

Como modelo de cálculo se va a emplear los datos de un camión volquete de dos ejes con una masa máxima en carga admisible (MMA) total del vehículo prevista para su matriculación/circulación por vías públicas de 3.500 kg.

Esta masa máxima admisible (MMA) supone el vehículo totalmente cargado y que incluye, además del peso del vehículo con su carrocería y su carga, los pesos del conductor, pasajeros y dotación completa de combustibles, lubricantes, herramientas, etc. Representa el peso máximo que el vehículo reglamentariamente NO puede superar para poder circular, en ningún caso.

A continuación se adjunta la siguiente tabla resumen con las masas máximas autorizadas (total del vehículo y por ejes) que se va a seguir como modelo de cálculo.

Recordar, que las masas aquí incluidas no podrán ser superadas en ningún caso por el diseño propuesto del vehículo durante su uso normal:

 

Por último, en esta otra tabla se incluyen los valores del peso en autobastidor o en chasis-cabina del vehículo de referencia (Q'):

 

2.2- Características del bastidor del vehículo

Como se sabe, todo camión o vehículo industrial dispone de una estructura portante tras la cabina, llamado bastidor o autobastidor, formada por dos largueros en acero, generalmente con perfil de sección en forma de  " [ " , que se encargan de recibir el peso de la carga y transmitirla a los ejes del vehículo.

Sin embargo, antes de montar la carrocería final sobre el vehículo conviene reforzar la estructura del autobastidor con otra estructura de refuerzo, llamada sobrebastidor auxiliar o falso bastidor, y que se monta sobre el autobastidor original del vehículo.

Durante el montaje, los largueros del falso bastidor se ajustarán perfectamente sobre los perfiles del bastidor del vehículo en toda su longitud. Con ello se conseguirá una distribución y transmisión uniforme de las cargas desde la carrocería hacia el bastidor del vehículo, además de garantizar una correcta fijación y anclaje de la carrocería a la estructura portante del vehículo.

Como norma general, para la fabricación del sobrebastidor auxiliar, se deberán emplear materiales, en este caso acero, de características iguales ó superiores al tipo de acero empleado en la fabricación del bastidor del vehículo.

En los casos que se requieran esfuerzos más elevados, o cuando se desee evitar secciones de gran altura en el perfil del sobrebastidor, entonces sí será obligatorio utilizar materiales de características superiores a los empleados en el bastidor del vehículo.

En todo caso, se recomienda que el acero empleado para la elaboración del falso del bastidor tenga también unas buenas propiedades para la soldadura.

En general, la calidad del tipo de acero recomendado, para todos los casos, será como mínimo St-52-3.

 

A continuación se muestra en la siguiente figura, una sección transversal de los perfiles que conforman los largueros de la estructura del autobastidor y sobrebastidor del vehículo, que se ha tomado como modelo para el cálculo en este tutorial:

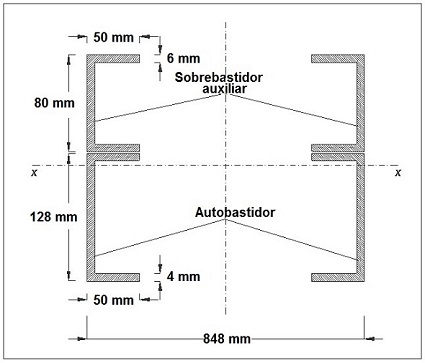
donde,

h₁ = 128 mm,  es la altura del alma del perfil que forma el autobastidor.

b₁ = 50 mm,  es la anchura del ala del perfil que forma el autobastidor.

e₁ = 4 mm,  es el espesor de pared del perfil que forma el autobastidor.

h₂ = 80 mm,  es la altura del alma del perfil que forma el sobrebastidor auxiliar.

b₂ = 50 mm,  es la anchura del ala del perfil que forma el sobrebastidor auxiliar.

e₂ = 6 mm,  es el espesor de pared del perfil que forma el sobrebastidor auxiliar.

 

Por otro lado, para la comprobación por resistencia de la sección de la estructura portante que conforman tanto el autobastidor y el sobrebastidor auxiliar, será necesario conocer su módulo resistente respecto al eje x-x neutro de la sección que es el eje de flexión del perfil, tal como se muestra en la figura anterior.

El módulo resistente a flexión de la sección total de uno de los largueros reforzados, es decir, el formado por autobastidor más el sobrebastidor auxiliar, viene dada por la siguiente expresión:

donde,

I_xx   es el momento de inercia del perfil de un larguero del bastidor reforzado respecto al eje x-x neutro de la sección.

y_máx   es la distancia del eje neutro de la sección a la fibra más alejada de la misma.

De acuerdo a las dimensiones mostrada en la figura anterior correspondiente a los perfiles de la estructura portante empleada en el vehículo, los valores de las propiedades mecánicas de estos perfiles son las siguientes:

• Módulo resistente a flexión del perfil de un larguero (autobastidor+sobrabastidor auxiliar) respecto al eje x-x neutro de la sección total reforzada, W_x = 67 cm³.

• Módulo resistente a flexión del perfil de un larguero del autobastidor sin refuerzo, con respecto a su eje neutro x₁-x₁, cuyo valor es de W_x1 = 35 cm³.

• Módulo resistente a flexión del perfil de un larguero del sobrebastidor auxiliar, con respecto a su eje neutro x₂-x₂, cuyo valor es de W_x2 = 27 cm³.

• Momento de inercia del perfil de un larguero del autobastidor sin refuerzo, I_x1 = 221 cm⁴.

• Momento de inercia del perfil de un larguero del sobrebastidor auxiliar, I_x2 = 107 cm⁴.

 

2.3- Reparto de la carga por eje

En este apartado se calculará el reparto de cargas por eje del vehículo, cuando la caja de carga se encuentra inclinada un ángulo (α), es decir, es la posición en la cual el vehículo bascula la caja de carga.

Previo a ello, es necesario conocer la cuantía de las cargas que se van a considerar que actúan sobre el vehículo, las cuales serán las siguientes:

-  Tara del autobastidor del vehículo en chasis-cabina, Q'=1445 kg.

-  Carga debido a los ocupantes (3 ocupantes: conductor + 2 pasajeros), P = 225 kg (75 kg x 3).

-  Peso máximo admitido de la mercancía a transportar, incluyéndose en este valor el peso del carrozado instalado y de la caja de carga, Q = Q₁ + Q₂ =1830 kg.

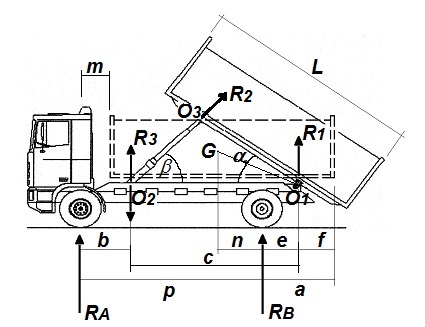
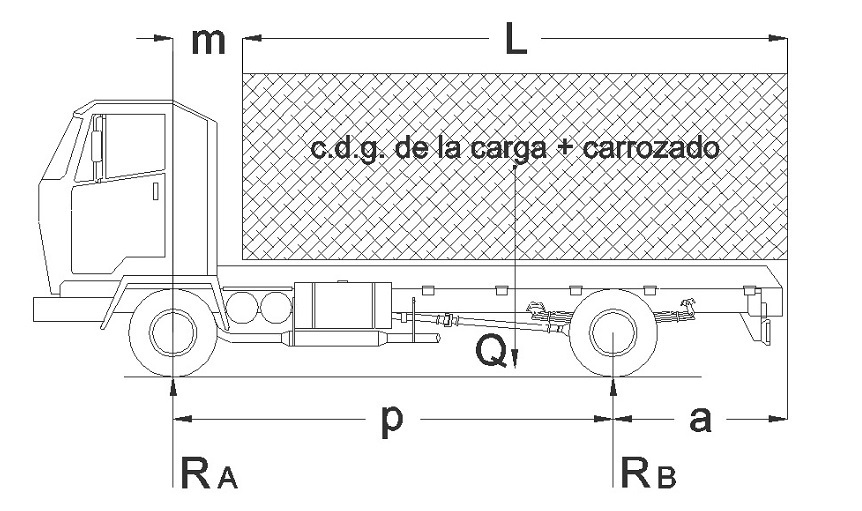
Por otro lado, los parámetros que van a intervenir en el cálculo del reparto de carga son los que a continuación se definen, de acuerdo a lo indicado en la figura adjunta:

L : es la longitud de la caja de carga.

a : es el voladizo posterior de la caja de carga medido desde el eje trasero del vehículo al extremo posterior de ésta.

p : es la distancia entre ejes del vehículo.

m : es la distancia medida desde el eje delantero al comienzo de la caja de carga.

O₁ : define el punto de articulación de la caja de carga, sobre el cual gira.

O₂ : es el punto donde se soporta el cilindro hidráulico elevador de la caja de carga en el bastidor del vehículo.

O₃ : define la posición del punto de empuje del cilindro elevador sobre la caja de carga.

α : indica el ángulo de giro de la caja de carga con respecto al bastidor, cuando está volteando.

δ : es el ángulo que forma con respecto al bastidor, la línea de unión de O₁  con el c.d.g. de la carga (punto G).

β : es el ángulo de inclinación del cilindro elevador con respecto al bastidor del vehículo.

c : indica la distancia entre los puntos O₁  y  O₂.

f : es la distancia entre el eje de articulación de la caja de carga (punto O₁) y el extremo posterior de ésta.

e : es la distancia entre el eje trasero del vehículo y el punto de articulación (O₁) de la caja de carga.

b : marca la distancia entre el eje delantero del vehículo y el punto de soporte del cilindro elevador O₂.

R₁ : representa el esfuerzo que se ejerce sobre el eje de articulación de la caja de carga.

R₂ : es el esfuerzo que se ejerce sobre la caja de carga debido al empuje del cilindro elevador.

R₃ : es la componente perpendicular sobre el bastidor del vehículo del esfuerzo de empuje del cilindro elevador.

Q : es el valor del peso del carrozado más la carga útil que transporta la caja (Q = Q₁ + Q₂).

A continuación, en la siguiente tabla se incluyen las medidas geométricas del vehículo que se ha tomado como referencia para servir de modelo de cálculo para este tutorial:

 

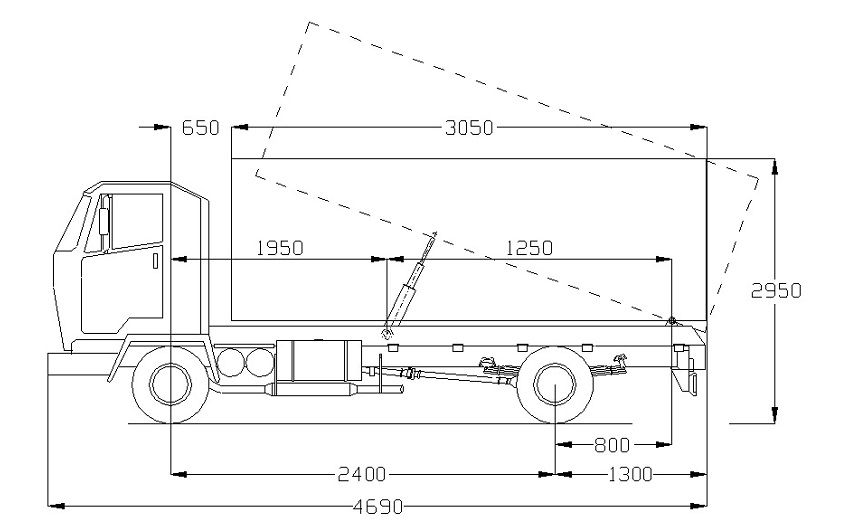
Medidas del vehículo carrozado

En la situación de vuelco de la caja de carga un ángulo de inclinación (α), las reacciones que se ejercen sobre el bastidor del vehículo en los puntos O₁  y  O₂, están expresadas mediante las siguientes formulaciones:

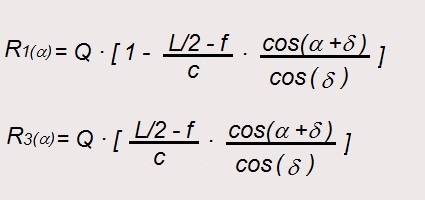
siendo, como se sabe,

R_1(α)   el esfuerzo que se ejerce sobre el bastidor del vehículo, para un ángulo de inclinación (α) de la caja de carga, en el punto del bastidor donde está situado el eje de articulación de la caja de carga (punto O₁).

R_3(α)   es el esfuerzo vertical sobre el bastidor del vehículo, para un ángulo de inclinación (α) de la caja de carga, en el punto del bastidor donde se sitúa el soporte del cilindro hidráulico elevador (punto O₂).

En este caso, se tiene además que el ángulo (δ) que forma con respecto al bastidor, la línea de unión de O₁ con el centro de gravedad de la carga (punto G), se puede expresar también como:

tg(δ) = h/(L/2-f), donde h es la altura del c.d.g. de la caja de carga, incluyendo la mercancía, respecto al bastidor del vehículo.

Aproximadamente, para la mayoría de los vehículos se tiene que el ángulo de inclinación máxima de una caja de carga durante su volteo es de 45º (α_máx = 45º), por lo que los cálculos de las reacciones sobre el vehículo se realizarán para este ángulo de inclinación (α = 45º).

Sustituyendo los valores de los parámetros que definen la geometría del vehículo, incluidos en la tabla 7 anterior, y para una inclinación de 45º de la caja de carga, se obtiene los siguientes valores para los esfuerzos R₁ y R₃ que se ejercen sobre el bastidor del vehículo:

R_1(α=45º) = 1830 · [1 - (3050/2-500)/1250 · (cos(45+δ)/cosδ)]

R_3(α=45º) = 1830 · [(3050/2-500)/1250 · (cos(45+δ)/cosδ)]

Por otro lado, como el ángulo (δ) se podía expresar también como:

tg(δ) = h/(L/2-f)

donde,

h es la altura del c.d.g. de la caja de carga, en este caso de valor h = 400 mm.

L = 3050 mm.

f = 500 mm.

Por lo que,

tg(δ) = h/(L/2-f) = 400/(3050/2-500) = 0,39

Resultando un ángulo, δ = 21º

Sustituyendo el valor del ángulo (δ = 21º) en las expresiones anteriores, las reacciones que se ejercen sobre el bastidor del vehículo para una inclinación (α = 45º) de la caja de carga resultarán ser las siguientes:

R_1(α=45º) = 1830 · [1 - (3050/2-500)/1250 · (cos(45+21)/cos(21))] =1176 Kg

R_3(α=45º) = 1830 · [(3050/2-500)/1250 · (cos(45+21)/cos(21))] = 654 Kg

Y por otro lado, las expresiones que permiten calcular las reacciones sobre los ejes delanteros (R_A) y traseros (R_B) del vehículo, cuando la caja de carga se encuentra inclinada un ángulo (α), son las siguientes:

siendo  n = h/tg(δ) - e

Sustituyendo los valores con las dimensiones del vehículo de la tabla 7, se obtiene que el parámetro  n  resultará:

n = h/tg(δ) - e = 400/0,39 - 800 = 226 mm.

Sustituyendo los valores del resto de parámetros, para un ángulo de inclinación de la caja de 45º (α = 45º), las reacciones que se obtienen sobre los ejes del vehículo resultarán ser las siguientes:

Se incluye la siguiente tabla resumen con la distribución de cargas obtenida por cada eje, para la situación de trabajo del vehículo con la caja de carga inclinada 45º y cargada, comprobándose que no se superan los límites establecidos, tanto por ejes como del total máximo permitido para el vehículo:

 

2.4- Cálculo de los esfuerzos cortantes y momentos flectores

El cálculo de las leyes de esfuerzos cortantes y de momentos flectores a lo largo del bastidor del vehículo se realiza estableciendo ecuaciones de equilibrio entre fuerzas (para el cálculo de los esfuerzos cortantes) y momentos (para el cálculo de la distribución de los momentos flectores).

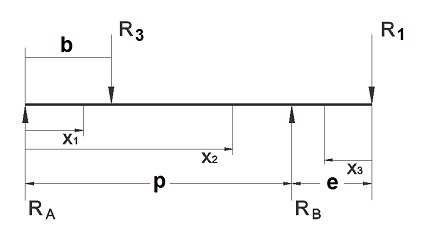
Según se representa en la figura adjunta, las fuerzas actuantes sobre el bastidor del vehículo son, por un lado, las reacciones que transmiten los ejes delantero (R_A) y trasero (R_B) del vehículo, y por otro lado, las reacciones R₁ (ejercida en el punto de articulación de la caja de carga - punto O₁) y R₃ (ejercida por el cilindro hidráulico elevador en el punto de soporte del bastidor - punto O₂).

Como siempre, la forma de proceder para establecer las leyes de esfuerzos y momentos es muy sencilla: se irá recorriendo la longitud del bastidor del vehículo por tramos, estableciéndose el equilibrio de fuerzas y momentos actuantes en cada tramo.

Para este caso, los distintos tramos en que se dividirá la longitud del bastidor serán los siguientes:

• Tramo I:  para b ≥ x₁ > 0; siendo b = 1,95 m, la distancia entre el eje delantero del vehículo y el punto de soporte del cilindro elevador (O₂), según se indicaba en la Tabla 7 con las dimensiones geométricas del vehículo. Por tanto, el Tramo I abarca desde la posición del eje delantero hasta el punto del bastidor donde se soporta el actuador hidráulico.

• Tramo II:  para p ≥ x₂ > b; siendo p = 2,40 m, la distancia entre los ejes delantero y trasero del vehículo, según se indicaba también en la Tabla 7. Este Tramo II abarca el tramo de bastidor desde el soporte del cilindro hidráulico (punto O₂) hasta el punto del bastidor donde se sitúa el eje trasero del vehículo.

• Tramo III:  para e ≥ x₃ > 0; siendo e = 0,80 m, la distancia entre el eje trasero y el punto de articulación de la caja de carga (O₁), según se indicaba en la Tabla 7. El Tramo III abarca la parte final del bastidor desde el eje trasero del vehículo hasta la posición del bulón de giro de la caja de carga.

A continuación se establecerán las ecuaciones de equilibrio, según los tramos en que queda dividido el bastidor del vehículo, a fin de obtener las leyes de esfuerzos cortantes y de momentos flectores que actúan sobre el bastidor del vehículo:

• Tramo I:

Para x₁= 0:

V(0)= R_A= -269 kg

M(0)= 0;

Para b= 1,95 m. ≥ x₁ > 0:

V(x₁)= R_A= -269 kg

M(x₁)= R_A·x₁= -269·x₁      (m·kg);

siendo  M_máx= -525 m·kg,  para x₁= 1,95 m.

 

• Tramo II:

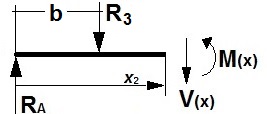
Para x₂= b= 1,95 m:

V(1,95)= R_A - R₃= -269-654= -923 kg

M(1,95)= R_A·b= -269·1,95= -525 m·kg

Para p= 2,40 m ≥ x₂ > b= 1,95 m:

V(x₂)= R_A-R₃= -923 kg

M(x₂)= R_A·x₂-R₃·(x₂-b)= -269·x₂-654·(x₂-1,95)      (m·kg)

siendo  M_máx= -940 m·kg,  para x₂= 2,40 m.

 

• Tramo III:

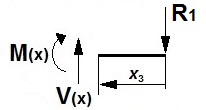
Para x₃= 0:

V(0)= R₁= 1176 kg

M(0)= 0 m·kg

Para e= 0,80 m ≥ x₃ > 0:

V(x₃)= R₁= 1176 kg

M(x₃)= -R₁·(x₃)= -1176·(x₃)      (m·kg)

siendo  M_máx= -940 m·kg,  para x₃= 0,80 m.

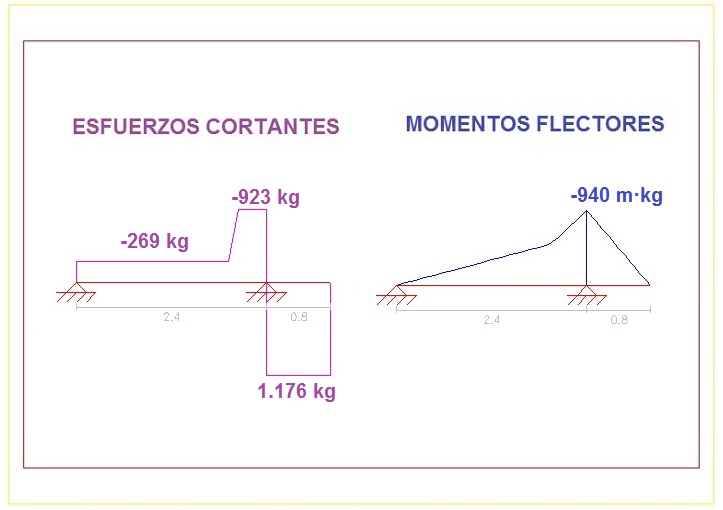
A continuación, se realiza una representación gráfica de las anteriores formulaciones para visualizar mejor cómo es la distribución de los esfuerzos cortantes y de los momentos flectores sobre el bastidor del vehículo, con objeto de poder apreciar mejor el tramo de bastidor donde se alcanzan los valores máximos:

GRÁFICOS DE ESFUERZOS Y MOMENTOS

 

2.5- Comprobación por resistencia del bastidor del vehículo

Para la comprobación por resistencia del bastidor del vehículo se debe, en primer lugar, identificar el sitio del bastidor donde se alcancen los esfuerzos más desfavorables.

Este caso se trata de un vehículo con la caja de carga en situación de volteo inclinada un ángulo de 45º, y según se muestra en los gráficos de distribución de esfuerzos del apartado anterior, el lugar del bastidor más desfavorable coincide con la posición del eje trasero del vehículo.

En este punto y según el apartado 2.4 anterior, los valores en valor absoluto de los esfuerzos obtenidos son los siguientes:

• Momento flector máximo, M = 940 m·kg

• Esfuerzo cortante máximo, V = 1.176 kg

 

Una vez identificado los esfuerzos máximos, se procede a calcular los valores de tensión (normal y de cortadura) que genera en la sección del bastidor estos esfuerzos:

-  Tensión normal a la sección debida al momento flector, o tensión de flexión (σ_f):

La tensión de trabajo a flexión que se produce en la sección del bastidor debida al momento flector (M) actuante viene dada por la siguiente expresión:

siendo,

M  el valor del momento flector que actúa en ese punto del bastidor, de valor M = 940 m·kg (94000 cm·kg)

W_x  es el módulo resistente a flexión de la sección de un larguero del bastidor reforzado del vehículo, es decir, bastidor+sobrabastidor auxiliar, respecto al eje x-x neutro de la sección. Este valor, según se vio en el apartado 2.2 anterior para el bastidor empleado en el vehículo, es de W_x= 67 cm³.

En la expresión anterior aparece en el denominador  2·W_x  debido a que el esfuerzo es resistido por los dos largueros que constituyen el bastidor del vehículo y sobre los que se apoya la caja de carga.

Sustituyendo valores se tiene que,

Resultando,

σ_f =  701 kg/cm²

 

-  Tensión de cortadura (τ):

Por otro lado, todo esfuerzo cortante (V_z) genera una tensión de cortadura o tensión tangencial (τ) en la sección del perfil, que en el caso de un perfil abierto de pared delgada, viene determinado por la siguiente expresión:

donde,

V_z  es el esfuerzo cortante que actúa en la sección del perfil

S_x  es el momento estático de media sección respecto al eje x de flexión

e  es el espesor de pared del perfil que constituye la sección del perfil

I_xx  es el momento de inercia de la sección del perfil respecto al eje x de flexión.

La tensión de cortadura será máxima en el eje x-x neutro de la sección, y nula en los extremos superior e inferior de la sección. En la siguiente figura se muestra el valor de las tensiones de cortadura máxima (τ_máx) para los tipos de secciones de bastidor más comúnmente empleadas en aplicaciones de reformas en vehículos. En todos los casos, el esfuerzo cortante (V_z) actúa siempre paralelo al eje z vertical y pasa por la línea que contiene al centro de esfuerzos cortantes de la sección.

Como se ve en la figura anterior, en los perfiles estructurales abiertos de pared delgada, como es el tipo  [  empleado en el bastidor del vehículo, el esfuerzo cortante es absorbido casi en su totalidad por el alma que constituye la pared vertical del perfil, siendo prácticamente nula la aportación de las alas horizontales del perfil en resistir la acción del cortante.

Por lo tanto, y teniendo en cuenta además que el esfuerzo cortante (V) actuante tiene que ser absorbido por los dos largueros que conforman el bastidor del vehículo, la tensión de cortadura (τ) máxima que se genera en cada larguero del bastidor, se puede expresar como:

donde,

A_c  es la denominada área de cortadura de la sección del bastidor, que es la que absorbe todo el esfuerzo cortante.

Por tanto, para perfiles de pared delgada con secciones en  [ , el área de cortadura puede ser obtenida por la siguiente expresión: A_c = 2/3·h·e, siendo "e" el espesor de pared del perfil, y "h" es la altura del alma del perfil.

De manera que el valor de la tensión de cortadura máxima que se produce en la sección del bastidor se podrá calcular también como:

Como ya se indicó en el apartado 2.2, para reforzar el autobastidor original del vehículo, se ha superpuesto encima otro sobrebastidor auxiliar con objeto de mejorar la resistencia del conjunto, según se indicaba en la figura del apartado 2.2 anterior donde se muestra una sección transversal de los perfiles que conforman los largueros de la estructura del autobastidor y sobrebastidor del vehículo.

En este caso, la altura total del alma del bastidor reforzado será la suma de la altura del alma del bastidor original del vehículo más la del sobrebastidor auxiliar, es decir, h = h₁ + h₂, según la citada figura del apartado 2.2.

En definitiva, aplicando la expresión que proporciona la tensión máxima de cortadura (τ), resulta:

donde,

V  es el esfuerzo cortante que actúa sobre el bastidor en el punto más desfavorable, de valor V = 1.176 kg, según se vio al principio del apartado

h  es la altura total del alma del bastidor reforzado, de valor h = h₁+h₂ = 128 + 80 = 208 mm (20,8 cm)

e  es el espesor de pared del alma del bastidor, de valor e = 4 mm (0,4 cm)

Sustituyendo estos valores en la expresión anterior, se tiene que:

Resultando finalmente, una tensión de cortadura máxima de valor:

τ =  106 kg/cm²

Una vez calculados los valores de las tensiones normales debida a la flexión (σ_f) y tangenciales (τ) máximas, la tensión de comparación (σ_co), o tensión de Von Mises, viene dada por la conocida expresión siguiente:

σ_co = (σ_f² + 3· τ² )^1/2

que sustituyendo los valores obtenidos resulta una tensión de comparación de:

σ_co = (701² + 3· 106² )^1/2 =  725 kg/cm²

Tomando como referencia el límite elástico del material del que está fabricado el bastidor y refuerzo, se debe cumplir siempre que:

σ_co < σ_e

donde (σ_e) es el límite elástico del acero empleado para fabricar el bastidor del vehículo. Según el apartado 1.2 donde se describían las características y propiedades del bastidor del vehículo, el límite elástico del acero empleado es de,

σ_e = 36 kg/mm² = 3600 kg/cm²

Por lo que se cumple que,

σ_co = 725 kg/cm² < σ_e = 3600 kg/cm²

Por último, el coeficiente de seguridad obtenido para el trabajo conjunto del bastidor reforzado vendrá dado por:

λ = σ_e /σ_co = 3600/725 = 4,9 > 3

Se recomienda, como medida de seguridad estructural, que el coeficiente de seguridad que se obtenga para el bastidor reforzado del vehículo sea mayor a 3  (λ = σ_e /σ_co > 3), como efectivamente así se cumple en nuestro ejemplo.

3- Caso C: Camión con Plataforma Elevadora de Carga Trasera

3.1- Modelo de cálculo del vehículo

En este caso se tratará de calcular la distribución de esfuerzos sobre el bastidor de un vehículo, que lleva instalado en la parte posterior una plataforma elevadora de carga, con objeto de facilitar la carga y descarga de mercancía de la caja de carga del camión.

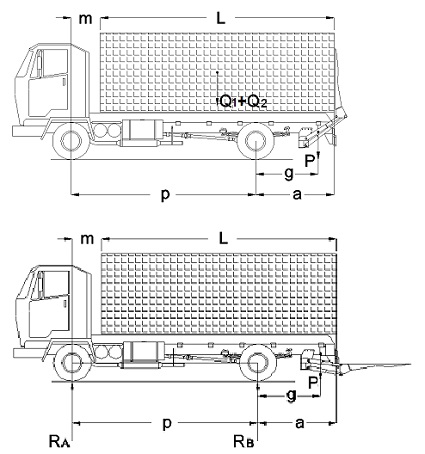
La plataforma instalada en el camión será de tipo retráctil, de manera que permanece plegada sobre el portón trasero de la caja de carga en situación de marcha del vehículo, para que éste pueda circular.

Con el vehículo parado, la plataforma se desplegará hasta colocarse en posición horizontal mediante la acción de pistones extensibles.

Una vez la plataforma en posición horizontal, ésta podrá iniciar los movimientos de elevación o descenso para la carga y descarga de mercancía de la caja de carga del camión.

Una vez descrito el tipo de carrocería, y con objeto de poder calcular la distribución de esfuerzos que genera la instalación de la plataforma elevadora de carga, se definirán los distintos pesos que actúan sobre el vehículo:

Q'   va a servir para designar el peso en autobastidor del vehículo, es decir, el peso del camión sin carrozar o en chasis-cabina.

Q₁   designará el peso de la caja de carga y de los largueros y travesaños que conforman el sobrebastidor auxiliar de refuerzo del chasis.

Q₂   será el peso máximo de mercancía que pueda transportar el vehículo en la caja de carga, es decir, será la carga útil.

P   es el peso propio de la plataforma elevadora de carga, incluyendo el equipo y auxiliares para el accionamiento de los movimientos de elevación y descenso de la plataforma.

Como siempre, se denomina TARA del vehículo a la que resulta de sumarle al peso en autobastidor o chasis cabina (Q'), el peso de la nueva carrocería montada (Q₁) y de la plataforma elevadora (P), incluyendo la dotación completa de combustible, lubricantes y herramientas del vehículo, es decir,

TARA = Q' + Q₁ + P + S

siendo "S" el peso de la dotación completa de combustible, lubricantes, fluidos hidráulicos, herramientas y rueda de repuesto.

Si se denominan R'_A y R'_B los pesos que gravitan por separado sobre los ejes delantero y trasero respectivamente, debido al peso en autobastidor del vehículo, entonces se tendrá que: Q' = R'_A + R'_B

Y por otro lado, también se denominará Q = Q₁ + Q₂, siendo (Q) la suma del peso propio de la caja de carga (Q₁) más la mercancía o carga útil que pueda transportar (Q₂).

Como modelo de cálculo se va a emplear los datos de un camión para el reparto de mercancía de dos ejes con una masa máxima en carga admisible (MMA) total del vehículo prevista para su matriculación/circulación por vías públicas de 6.500 kg.

Esta masa máxima admisible (MMA) supone el vehículo totalmente cargado y que incluye, además del peso del vehículo con su carrocería, plataforma elevadora y su carga, los pesos del conductor, pasajeros y dotación completa de combustibles, lubricantes, herramientas, etc. Representa el peso máximo que el vehículo reglamentariamente NO puede superar para poder circular, en ningún caso.

A continuación se adjunta la siguiente tabla resumen con las masas máximas autorizadas (total del vehículo y por ejes) que se va a seguir como modelo de cálculo.

 

En esta otra tabla se incluyen los valores del peso propio del vehículo en autobastidor o chasis-cabina (Q'):

 

Por otro lado, la plataforma elevadora retráctil que va instalada en la parte trasera del vehículo responde a las siguientes características técnicas:

 

3.2- Características del bastidor del vehículo

Como se sabe, todo camión o vehículo industrial dispone de una estructura portante tras la cabina, llamado bastidor o autobastidor, formada por dos largueros en acero, generalmente con perfil de sección en forma de  " [ " , que se encargan de recibir el peso de la carga y transmitirla a los ejes del vehículo.

Sin embargo, antes de montar la carrocería final sobre el vehículo conviene reforzar la estructura del autobastidor con otra estructura de refuerzo, llamada sobrebastidor auxiliar o falso bastidor, y que se monta sobre el autobastidor original del vehículo.

Durante el montaje, los largueros del falso bastidor se ajustarán perfectamente sobre los perfiles del bastidor del vehículo en toda su longitud. Con ello se conseguirá una distribución y transmisión uniforme de las cargas desde la carrocería hacia el bastidor del vehículo, además de garantizar una correcta fijación y anclaje de la carrocería a la estructura portante del vehículo.

Como norma general, para la fabricación del sobrebastidor auxiliar, se deberán emplear materiales, en este caso acero, de características iguales ó superiores al tipo de acero empleado en la fabricación del bastidor del vehículo.

En los casos que se requieran esfuerzos más elevados, o cuando se desee evitar secciones de gran altura en el perfil del sobrebastidor, entonces sí será obligatorio utilizar materiales de características superiores a los empleados en el bastidor del vehículo.

En todo caso, se recomienda que el acero empleado para la elaboración del falso del bastidor tenga también unas buenas propiedades para la soldadura.

En general, la calidad del tipo de acero recomendado, para todos los casos, será como mínimo St-52-3.

 

A continuación se muestra en la siguiente figura, una sección transversal de los perfiles que conforman los largueros de la estructura del autobastidor y sobrebastidor del vehículo, que se ha tomado como modelo para el cálculo en este tutorial:

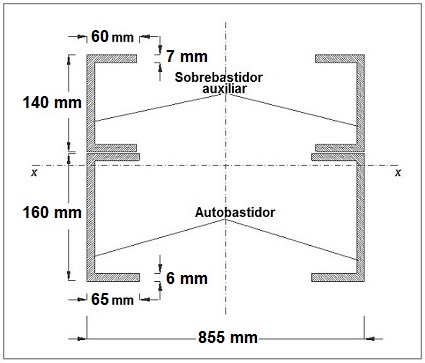
donde,

h₁ = 160 mm,  es la altura del alma del perfil que forma el autobastidor.

b₁ = 65 mm,  es la anchura del ala del perfil que forma el autobastidor.

e₁ = 6 mm,  es el espesor de pared del perfil que forma el autobastidor.

h₂ = 140 mm,  es la altura del alma del perfil que forma el sobrebastidor auxiliar.

b₂ = 60 mm,  es la anchura del ala del perfil que forma el sobrebastidor auxiliar.

e₂ = 7 mm,  es el espesor de pared del perfil que forma el sobrebastidor auxiliar.

 

Por otro lado, para la comprobación por resistencia de la sección de la estructura portante que conforman tanto el autobastidor y el sobrebastidor auxiliar, será necesario conocer su módulo resistente respecto al eje x-x neutro de la sección que es el eje de flexión del perfil, tal como se muestra en la figura anterior.

El módulo resistente a flexión de la sección total de uno de los largueros reforzados, es decir, el formado por autobastidor más el sobrebastidor auxiliar, viene dada por la siguiente expresión:

donde,

I_xx   es el momento de inercia del perfil de un larguero del bastidor reforzado respecto al eje x-x neutro de la sección.

y_máx   es la distancia del eje neutro de la sección a la fibra más alejada de la misma.

De acuerdo a las dimensiones mostrada en la figura anterior correspondiente a los perfiles de la estructura portante empleada en el vehículo, los valores de las propiedades mecánicas de estos perfiles son las siguientes:

• Módulo resistente a flexión del perfil de un larguero (autobastidor+sobrabastidor auxiliar) respecto al eje x-x neutro de la sección total reforzada, W_x = 189 cm³.

• Módulo resistente a flexión del perfil de un larguero del autobastidor sin refuerzo, con respecto a su eje neutro x₁-x₁, cuyo valor es de W_x1 = 83 cm³.

• Módulo resistente a flexión del perfil de un larguero del sobrebastidor auxiliar, con respecto a su eje neutro x₂-x₂, cuyo valor es de W_x2 = 72 cm³.

• Momento de inercia del perfil de un larguero del autobastidor sin refuerzo, I_x1 = 662 cm⁴.

• Momento de inercia del perfil de un larguero del sobrebastidor auxiliar, I_x2 = 507 cm⁴.

 

3.3- Reparto de la carga por eje

Previo a realizar el análisis de los esfuerzos que actúan sobre la estructura portante del vehículo, es necesario conocer cómo se distribuyen los pesos de la plataforma elevadora trasera, y de la caja de carga más la carga útil transportada, sobre cada eje del vehículo.

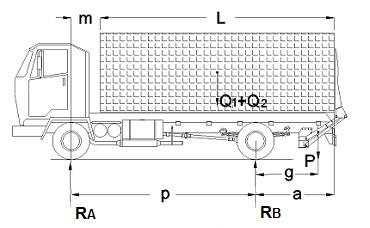
Como sabemos de apartados anteriores, con Q₁ se denominaba el peso de la carrocería formada por la caja de carga y Q₂ es el peso máximo de la mercancía que puede transportar el camión o carga útil.

Entonces, se llamará Q a la suma de ambos, es decir, al peso del carrozado de la caja de carga más la carga útil que ésta puede transportar:

Q = Q₁ + Q₂

A continuación se expondrá las formulaciones que permiten calcular las reacciones que se originan en cada eje del vehículo.

 

Para vehículos 4x2 en posición de marcha, con la carga uniformemente repartida sobre la caja de carga, y considerando el peso de la plataforma instalada concentrado en su centro de gravedad (c.d.g.), el cálculo de las reacciones sobre los ejes del vehículo, delantero (R_A) y trasero (R_B), viene dado por las siguientes expresiones:

donde:

L   es la longitud de la caja de carga, en mm.

a   es el voladizo posterior de la caja de carga, en mm.

p   es la distancia entre ejes del vehículo, en mm.

m   es la distancia desde el eje delantero al comienzo de la caja de carga, en mm.

g   es la distancia del c.d.g. de la plataforma elevadora al eje trasero del vehículo, en mm.

P   es el peso de la plataforma elevadora aplicada en su c.d.g., en kg.

Q   es el valor del peso de la caja de carga más la carga útil que puede transportar, en kg. (Q = Q₁ + Q₂).

Las expresiones anteriores que proporcionan las reacciones sobre los ejes del vehículo, son el resultado de aplicar equilibrio de las fuerzas y momentos actuantes. En esta ocasión se está considerando que la mercancía o carga útil que transporta el vehículo se distribuye uniformemente a lo largo de la caja de carga, resultando así aplicada su resultante en el centro de gravedad (c.d.g.) de la caja de carga.

Por otro lado, el peso propio de la plataforma elevadora y sus auxiliares también se considera aplicado en el c.d.g. del conjunto de la plataforma, que está situado una distancia "g" del eje trasero del vehículo.

En la siguiente tabla se incluyen las medidas geométricas del vehículo carrozado con la plataforma:

 

Por otro lado, la masa máxima en carga admisible prevista para matriculación/circulación (MMA) del vehículo de referencia para este tutorial, según está indicado en el apartado 3.1 anterior, es de 6.500 kg.

Asimismo, el peso del vehículo en chasis-cabina (Q') es de 2.216 kg, igualmente indicado en el apartado 3.1 anterior.

De la propia definición de la masa máxima admisible (MMA) del vehículo se tiene que,

MMA = Q' + Ocupantes + P + Q₁ + Q₂ = Q' + Ocupantes + P + Q

Como MMA = 6.500 kg, Ocupantes = 75 kg, P (peso propio de la plataforma) = 431 kg  y  Q' = 2.216 kg, entonces se tiene que,

Q = MMA - Q' - Ocupantes - P = 6500 - 2216 - 75 - 431 = 3778 kg

Por tanto, aplicando los valores de las dimensiones del vehículo de la tabla 10 anterior y con la carga Q = 3.778 kg, las expresiones de cálculo de las reacciones en los ejes del vehículo quedan como sigue:

Resultando:

R_A = 394 kg

R_B = 3815 kg

Se incluye la siguiente tabla resumen con la distribución de cargas obtenida por cada eje, comprobándose que no se superan los límites establecidos, tanto por ejes como del total máximo permitido para el vehículo:

 

3.4- Cálculo de los esfuerzos cortantes y momentos flectores

El cálculo de las leyes de esfuerzos cortantes y de momentos flectores a lo largo del bastidor del vehículo se realiza estableciendo ecuaciones de equilibrio entre fuerzas (para el cálculo de los esfuerzos cortantes) y momentos (para el cálculo de la distribución de los momentos flectores).

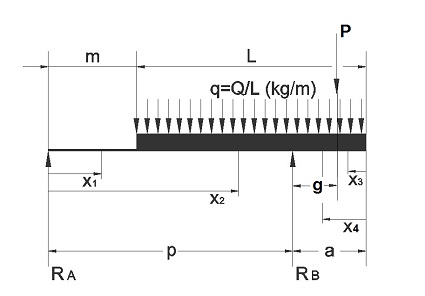
Según se representa en la figura adjunta, las fuerzas actuantes sobre el bastidor del vehículo son, por un lado, las reacciones que transmiten los ejes delantero (R_A) y trasero (R_B) del vehículo, y por otro lado, el peso propio de la caja de carga (Q₁) más la carga útil (Q₂), que como ya se vio anteriormente, su suma resulta la carga Q = Q₁ + Q₂, más la carga actuante debida al peso propio de la plataforma elevadora (P).

Asimismo, la carga Q (kg) se supone uniformemente distribuida a lo largo de la caja de carga, pudiéndose expresar como una carga lineal (q) que actúa en toda la longitud de la caja de carga de valor, q = Q/L (kg/m), siendo L la longitud de la caja de carga.

Por otro lado, el peso propio de la plataforma elevadora (P) se considera como una carga puntual aplicada en el c.d.g. del conjunto de la plataforma, que está situado una distancia "g" del eje trasero del vehículo.

Como siempre, la forma de proceder para establecer las leyes de esfuerzos y momentos es muy sencilla: se irá recorriendo la longitud del bastidor del vehículo por tramos, estableciéndose el equilibrio de fuerzas y momentos actuantes en cada tramo.

Para este caso, los distintos tramos en que se dividirá la longitud del bastidor serán los siguientes:

• Tramo I:  para m ≥ x₁ > 0; siendo m = 1,41 m, la distancia desde el eje delantero al comienzo de la caja de carga, según se indicaba en la Tabla 10 "Dimensiones geométricas del vehículo carrozado". Por tanto, el Tramo I abarca desde la posición del eje delantero hasta el punto del bastidor donde comienza la caja de carga.

• Tramo II:  para p ≥ x₂ > m; siendo p = 4,13 m, la distancia entre los ejes delantero y trasero del vehículo, según se indicaba también en la Tabla 10. Este Tramo II abarca el tramo de bastidor desde el comienzo de la caja de carga hasta el punto del bastidor donde se sitúa el eje trasero del vehículo.

• Tramo III:  para a-g ≥ x₃ > 0; siendo a = 1,55 m, el voladizo posterior de la caja de carga, y g = 1,35 m la distancia del centro de gravedad (c.d.g.) de la plataforma al eje trasero, según se indicaba en la Tabla 10. El Tramo III abarca desde el extremo posterior de la caja de carga hasta la posición del c.d.g. de la plataforma elevadora.

• Tramo IV:  para a ≥ x₄ > g; abarca el tramo de bastidor desde la posición del eje trasero del vehículo hasta el punto del bastidor donde se sitúa el c.d.g. de la plataforma elevadora de carga.

A continuación se establecerán las ecuaciones de equilibrio, según los tramos en que queda dividido el bastidor del vehículo, a fin de obtener las leyes de esfuerzos cortantes y de momentos flectores que actúan sobre el bastidor del vehículo:

• Tramo I:

Para x₁=0:

V(0)= R_A= 394 kg

M(0)= 0;

Para m=1,41 m. ≥ x₁ > 0:

V(x₁)= R_A= 394 kg

M(x₁)= R_A·x₁= 394·x₁      (m·kg);

siendo  M_máx= 556 m·kg,  para x₁=1,41 m.

 

• Tramo II:

Para p=4,13 m ≥ x₂ > m=1,41 m:

V(x₂)= R_A-q·(x₂-m)= 394-884,78·(x₂-1,41);  de donde q= Q/L= 3778/4,27= 884,78 kg/m;

siendo  V_máx= -2013 kg,  para x₂= 4,13 m.

M(x₂)= R_A·x₂-q/2·(x₂-m)²= 394·x₂-442,39·(x₂-1,41)²      (m·kg)

siendo  M_máx= -1645 m·kg,  para x₂= 4,13 m.

 

• Tramo III:

Para a-g=0,20 m ≥ x₃ > 0:

V(x₃)= q·x₃= 884,78·x₃      (Kg)

siendo  V_máx= 177 kg,  para x₃=0,20 m.

M(x₃)= -q/2·(x₃)²= -442,39·(x₃)²      (m·kg)

siendo  M_máx= -18 m·kg,  para x₃=0,20 m.

 

• Tramo IV:

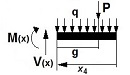
Para a=1,55 m ≥ x₄ > a-g=0,20 m.:

V(x₄)= P+q·x₄= 431+884,78·x₄      (Kg)

siendo  V_máx= 1802 kg,  para x₄=1,55 m.

M(x₄)= -P·(x₄-(a-g))-q/2·(x₄)²= -431·(x₄-0,20)-442,39·(x₄)²      (m·kg)

siendo  M_máx= -1645 m·kg,  para x₄=1,55 m.

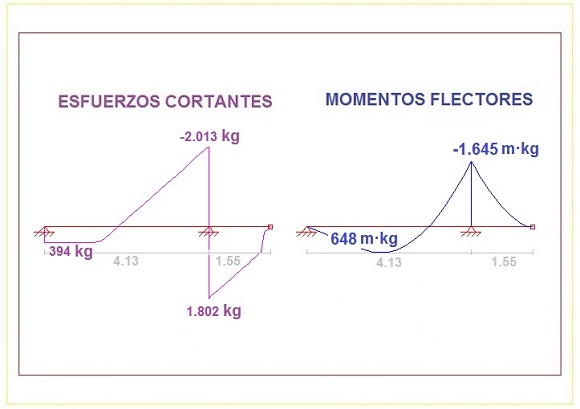
A continuación, se realiza una representación gráfica de las anteriores formulaciones para visualizar mejor cómo es la distribución de los esfuerzos cortantes y de los momentos flectores sobre el bastidor del vehículo, con objeto de poder apreciar mejor el tramo de bastidor donde se alcanzan los valores máximos:

GRÁFICOS DE ESFUERZOS Y MOMENTOS

 

3.5- Comprobación por resistencia del bastidor del vehículo

Para la comprobación por resistencia del bastidor del vehículo se debe, en primer lugar, identificar el sitio del bastidor donde se alcancen los esfuerzos más desfavorables.

En este caso, y según se muestra en los gráficos de distribución de esfuerzos del apartado anterior, coincide en el lugar del bastidor donde el eje trasero está situado.

En este punto y según el apartado 3.4 anterior, los valores en valor absoluto de los esfuerzos obtenidos son los siguientes:

• Momento flector máximo, M = 1.645 m·kg

• Esfuerzo cortante máximo, V = 2.013 kg

 

Una vez identificado los esfuerzos máximos, se procede a calcular los valores de tensión (normal y de cortadura) que genera en la sección del bastidor estos esfuerzos:

-  Tensión normal a la sección debida al momento flector, o tensión de flexión (σ_f):

La tensión de trabajo a flexión que se produce en la sección del bastidor debida al momento flector (M) actuante viene dada por la siguiente expresión:

siendo,

M  el valor del momento flector que actúa en ese punto del bastidor, de valor M = 1645 m·kg (164500 cm·kg)

W_x  es el módulo resistente a flexión de la sección de un larguero del bastidor reforzado del vehículo, es decir, bastidor+sobrabastidor auxiliar, respecto al eje x-x neutro de la sección. Este valor, según se vio en el apartado 3.2 anterior para el bastidor empleado en el vehículo, es de W_x= 189 cm³.

En la expresión anterior aparece en el denominador  2·W_x  debido a que el esfuerzo es resistido por los dos largueros que constituyen el bastidor del vehículo y sobre los que se apoya la caja de carga.

Sustituyendo valores se tiene que,

Resultando,

σ_f =  435 kg/cm²

 

-  Tensión de cortadura (τ):

Por otro lado, todo esfuerzo cortante (V_z) genera una tensión de cortadura o tensión tangencial (τ) en la sección del perfil, que en el caso de un perfil abierto de pared delgada, viene determinado por la siguiente expresión:

donde,

V_z  es el esfuerzo cortante que actúa en la sección del perfil

S_x  es el momento estático de media sección respecto al eje x de flexión

e  es el espesor de pared del perfil que constituye la sección del perfil

I_xx  es el momento de inercia de la sección del perfil respecto al eje x de flexión.

La tensión de cortadura será máxima en el eje x-x neutro de la sección, y nula en los extremos superior e inferior de la sección. En la siguiente figura se muestra el valor de las tensiones de cortadura máxima (τ_máx) para los tipos de secciones de bastidor más comúnmente empleadas en aplicaciones de reformas en vehículos. En todos los casos, el esfuerzo cortante (V_z) actúa siempre paralelo al eje z vertical y pasa por la línea que contiene al centro de esfuerzos cortantes de la sección.

Como se ve en la figura anterior, en los perfiles estructurales abiertos de pared delgada, como es el tipo  [  empleado en el bastidor del vehículo, el esfuerzo cortante es absorbido casi en su totalidad por el alma que constituye la pared vertical del perfil, siendo prácticamente nula la aportación de las alas horizontales del perfil en resistir la acción del cortante.

Por lo tanto, y teniendo en cuenta además que el esfuerzo cortante (V) actuante tiene que ser absorbido por los dos largueros que conforman el bastidor del vehículo, la tensión de cortadura (τ) máxima que se genera en cada larguero del bastidor, se puede expresar como:

donde,

A_c  es la denominada área de cortadura de la sección del bastidor, que es la que absorbe todo el esfuerzo cortante.

Por tanto, para perfiles de pared delgada con secciones en  [ , el área de cortadura puede ser obtenida por la siguiente expresión: A_c = 2/3·h·e, siendo "e" el espesor de pared del perfil, y "h" es la altura del alma del perfil.

De manera que el valor de la tensión de cortadura máxima que se produce en la sección del bastidor se podrá calcular también como:

Como ya se indicó en el apartado 3.2, para reforzar el autobastidor original del vehículo, se ha superpuesto encima otro sobrebastidor auxiliar con objeto de mejorar la resistencia del conjunto, según se indicaba en la figura del apartado 3.2 anterior donde se muestra una sección transversal de los perfiles que conforman los largueros de la estructura del autobastidor y sobrebastidor del vehículo.

En este caso, la altura total del alma del bastidor reforzado será la suma de la altura del alma del bastidor original del vehículo más la del sobrebastidor auxiliar, es decir, h = h₁ + h₂, según la citada figura del apartado 3.2.

En definitiva, aplicando la expresión que proporciona la tensión máxima de cortadura (τ), resulta:

donde,

V  es el esfuerzo cortante que actúa sobre el bastidor en el punto más desfavorable, de valor V = 2.013 kg, según se vio al principio del apartado

h  es la altura total del alma del bastidor reforzado, de valor h = h₁+h₂ = 160+140= 300 mm (30,0 cm)

e  es el espesor de pared del alma del bastidor, de valor e = 6 mm (0,6 cm)

Sustituyendo estos valores en la expresión anterior, se tiene que:

Resultando finalmente, una tensión de cortadura máxima de valor:

τ =  84 kg/cm²

Una vez calculados los valores de las tensiones normales debida a la flexión (σ_f) y tangenciales (τ) máximas, la tensión de comparación (σ_co), o tensión de Von Mises, viene dada por la conocida expresión siguiente:

σ_co = (σ_f² + 3· τ² )^1/2

que sustituyendo los valores obtenidos resulta una tensión de comparación de:

σ_co = (435² + 3· 84² )^1/2 =  459 kg/cm²

Tomando como referencia el límite elástico del material del que está fabricado el bastidor y refuerzo, se debe cumplir siempre que:

σ_co < σ_e

donde (σ_e) es el límite elástico del acero empleado para fabricar el bastidor del vehículo. Según el apartado 3.2 donde se describían las características y propiedades del bastidor del vehículo, el límite elástico del acero empleado es de,

σ_e = 36 kg/mm² = 3600 kg/cm²

Por lo que se cumple que,

σ_co = 459 kg/cm² < σ_e = 3600 kg/cm²

Por último, el coeficiente de seguridad obtenido para el trabajo conjunto del bastidor reforzado vendrá dado por:

λ = σ_e /σ_co = 3600/459 = 7,8 > 3

Se recomienda, como medida de seguridad estructural, que el coeficiente de seguridad que se obtenga para el bastidor reforzado del vehículo sea mayor a 3  (λ = σ_e /σ_co > 3), como efectivamente así se cumple en nuestro ejemplo.

 

 

>> FIN DEL TUTORIAL

 

 

Volver a
Tutoriales

 

 

Información y consulta:

Hermenegildo Rodríguez Galbarro

info@ingemecanica.com - Tel. 646 166 055