— Tutorial nº 100 —
Características Mecánicas del Acero
Índice de contenidos:
1- Introducción
2- Diagrama Tensión-Deformación
3- Límite elástico y Resistencia a la tracción
4- Módulo de elasticidad longitudinal o Módulo de Young
5- Módulo de elasticidad transversal
6- Coeficiente de Poisson
7- Estricción
8- Resiliencia
9- Tenacidad a la fractura
10- Dureza Brinell
11- Soldabilidad
12- Resistencia al desgarro
13- Aptitud al doblado
14- Otros datos de diseño (densidad, punto de fusión, dilatación lineal…)
ANEXOS:
Anexo 1.- Diagrama Hierro-Carbono (Fe-C)
Anexo 2.- Propiedades mecánicas de aceros estructurales según norma europea
Anexo 3.- Composición química de aceros estructurales según norma europea
Anexo 4.- Propiedades mecánicas de aceros estructurales según norma americana
Anexo 5.- Composición química de aceros estructurales según norma americana
TABLAS CON LOS TIPOS DE ACEROS Y SUS APLICACIONES:
>> Descarga en PDF - Aceros de Herramientas (Fuente: thyssenkrupp Materials Ibérica, S.A.)
>> Descarga en PDF - Aceros de Construcción (Fuente: thyssenkrupp Materials Ibérica, S.A.)
DESARROLLO DEL CONTENIDO
1- Introducción
Según la norma UNE EN 10020:2001 define al acero como aquel material en el que el hierro es el elemento predominante, el contenido en carbono es, generalmente inferior al 2% y contiene además a otros elementos.
El límite superior del 2% en el contenido de carbono (C) es el límite que separa al acero de la fundición. En general, un aumento del contenido de carbono en el acero eleva su resistencia a la tracción, pero como contrapartida incrementa su fragilidad en frío y hace que disminuya la tenacidad y la ductilidad. En función de este porcentaje, los aceros se pueden clasificar de la siguiente manera:
- Aceros dulce: Cuando el porcentaje de carbono es del 0,25% máximo. Estos aceros tienen una resistencia última de rotura en el rango de 48-55 kg/mm2 y una dureza Brinell en el entorno de 135-160 HB. Son aceros que presentan una buena soldabilidad aplicando la técnica adecuada.
Aplicaciones: Piezas de resistencia media de buena tenacidad, deformación en frío, embutición, plegado, herrajes, etc.
- Aceros semidulce: El porcentaje de carbono está en el entorno del 0,35%. Tiene una resistencia última a la rotura de 55-62 kg/mm2 y una dureza Brinell de 150-170 HB. Estos aceros bajo un tratamiento térmico por templado pueden alcanzar una resistencia mecánica de hasta 80 kg/mm2 y una dureza de 215-245 HB.
Aplicaciones: Ejes, elementos de maquinaria, piezas resistentes y tenaces, pernos, tornillos, herrajes.
- Aceros semiduro: Si el porcentaje de carbono es del 0,45%. Tienen una resistencia a la rotura de 62-70 kg/mm2 y una dureza de 280 HB. Después de someterlos a un tratamiento de templado su resistencia mecánica puede aumentar hasta alcanzar los 90 kg/mm2.
Aplicaciones: Ejes y elementos de máquinas, piezas bastante resistentes, cilindros de motores de explosión, transmisiones, etc.
- Aceros duro: El porcentaje de carbono es del 0,55%. Tienen una resistencia mecánica de 70-75 kg/mm2, y una dureza Brinell de 200-220 HB. Bajo un tratamiento de templado estos aceros pueden alcanzar un valor de resistencia de 100 kg/mm2 y una dureza de 275-300 HB.
Aplicaciones: Ejes, transmisiones, tensores y piezas regularmente cargadas y de espesores no muy elevados.
2- Diagrama Tensión-Deformación
El diagrama tensión-deformación resulta de la representación gráfica del ensayo de tracción, normalizado en UNE-EN 10002-1, y que consiste en someter a una probeta de acero normalizada a un esfuerzo creciente de tracción según su eje hasta la rotura de la misma. El ensayo de tracción permite el cálculo de diversas propiedades mecánicas del acero.
La probeta de acero empleada en el ensayo consiste en una pieza cilíndrica cuyas dimensiones guardan la siguiente relación de proporcionalidad:
L0= 5,65 · √S0
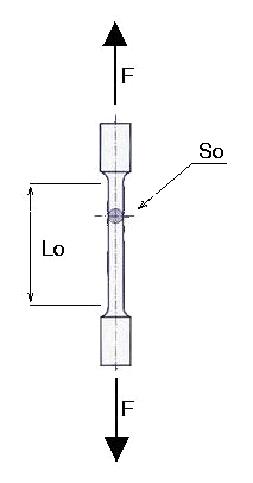
Donde L0 es la longitud inicial, S0 es la sección inicial y D0 es el diámetro inicial de la probeta. Para llevar a cabo el ensayo de tracción, las anteriores variables pueden tomar los siguientes valores:
D0 = 20 mm, L0 = 100 mm, ó bien,
D0 = 10 mm, L0 = 50 mm.
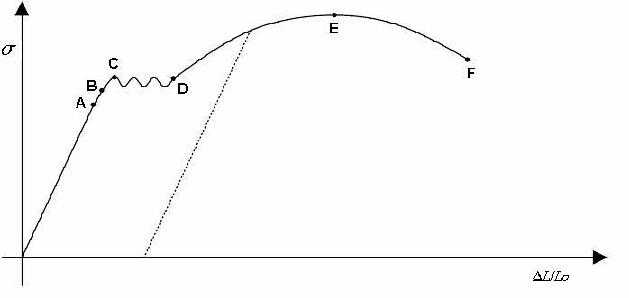
El ensayo comienza aplicando gradualmente la fuerza de tracción a la probeta, lo cual provoca que el recorrido inicial en la gráfica discurra por la línea recta que une el origen de coordenadas con el punto A.
Hasta llegar al punto A se conserva una proporcionalidad entre la tensión alcanzada y el alargamiento unitario producido en la pieza. Es lo que se conoce como Ley de Hooke, que relaciona linealmente tensiones con las deformaciones a través del modulo de elasticidad E, constante para cada material que en el caso de los aceros y fundiciones vale aproximadamente 2.100.000 Kg/cm2.
Otra particularidad de este tramo es que al cesar la solicitación sobre la pieza, ésta recupera su longitud inicial. Es decir, se comporta de manera elástica, y el punto A se denomina Límite de Proporcionalidad.
Pasado el punto A y hasta llegar al punto B, los alargamiento producidos incluso crecen de manera más rápida con la tensión, y se cumple que al cesar la carga, la pieza recupera de nuevo su geometría inicial, es decir, se sigue comportando elásticamente. El punto B marca el límite a este comportamiento, y por ello al punto B se le denomina Límite Elástico.
Traspasado el punto B el material pasa a comportarse de manera plástica, es decir, que no recupera su longitud inicial, quedando una deformación remanente al cesar la carga. De esta manera, el proceso de descarga se realiza siguiendo la trayectoria según la línea punteada mostrada del diagrama tensión-deformación, que como se ve, corta al eje de deformaciones, ΔL/L0, a una cierta distancia del origen, que se corresponde con la deformación remanente que queda. Concretamente, el punto B o Límite Elástico es aquel que le corresponde una deformación remanente del 0.2%.
Si se sigue aplicando carga se llega al punto identificado en la gráfica como C, donde a partir de aquí y hasta el punto D, las deformaciones crecen de manera rápida mientras que la carga fluctúa entre dos valores, llamados límites de fluencia, superior e inferior. Este nuevo estadio, denominado de fluencia, es característico exclusivamente de los aceros dúctiles, no apareciendo en los aceros endurecidos.
Más allá del punto de fluencia D es necesario seguir aplicando un aumento de la carga para conseguir un pronunciado aumento del alargamiento. Entramos ya en la zona de las grandes deformaciones plásticas hasta alcanzar el punto F, donde la carga alcanza su valor máximo, lo que dividida por el área inicial de la probeta proporciona la tensión máxima de rotura o resistencia a la tracción.
A partir del punto E tiene lugar el fenómeno de estricción de la probeta, consistente en una reducción de la sección en la zona de la rotura, y el responsable del periodo de bajada del diagrama, dado que al reducirse el valor de la sección real, el valor de la carga aplicado a partir del punto E también se va reduciendo hasta alcanzar el punto F de rotura.
3- Límite elástico y Resistencia a la tracción
La determinación de las propiedades mecánicas en el acero, como el límite elástico (fy), la resistencia a tracción (fu), así como de otras características mecánicas del acero como el Módulo de Elasticidad (E), o el alargamiento máximo que se produce en la rotura, se efectuará mediante el anteriormente definido ensayo de tracción normalizado en la UNE-EN 10002-1.
El valor de la tensión última o resistencia a la tracción se calcula a partir de este ensayo, y se define como el cociente entre la carga máxima que ha provocado el fallo a rotura del material por tracción y la superficie de la sección transversal inicial de la probeta, mientras que el límite elástico marca el umbral que, una vez se ha superado, el material trabaja bajo un comportamiento plástico y deformaciones remanente.
En la sección ANEXOS de este tutorial se pueden consultar los valores del límite elástico y la resistencia a tracción para las distintas calidades de aceros según las normativas europea y americana.
Se adjunta tabla con los valores de la resistencia a la tracción, así como del límite elástico y dureza, según la norma americana AISI:
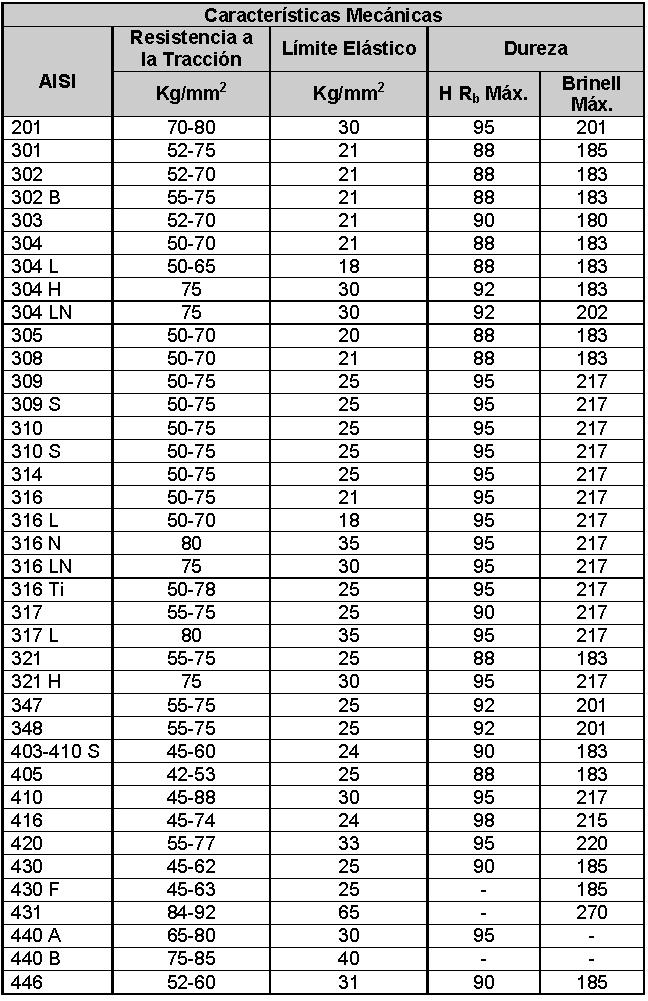
A continuación, en estas otras tablas se recogen también las especificaciones correspondientes al límite elástico (fy) y resistencia a tracción (fu) para los distintos tipos de acero según se indican en la Instrucción de Acero Estructural (EAE) española.
• Aceros no aleados laminados en caliente:
| Límite elástico mínimo y Resistencia a tracción (N/mm2) | ||||
| Tipo | Espesor nominal de la pieza, t (mm) | |||
| t ≤ 40 | 40 < t ≤ 80 | |||
| Límite elástico, fy | Resistencia a tracción, fu | Límite elástico, fy | Resistencia a tracción, fu | |
| S 235 | 235 | 360 < fu < 510 | 215 | 360 < fu < 510 |
| S 275 | 275 | 430 < fu < 580 | 255 | 410 < fu < 560 |
| S 355 | 355 | 490 < fu < 680 | 335 | 470 < fu < 630 |
En los siguientes apartados se definen las características resistentes para los aceros con características especiales:
• Aceros soldables de grano fino, en la condición de normalizado:
| Límite elástico mínimo y Resistencia a tracción (N/mm2) | ||||
| Tipo | Espesor nominal de la pieza, t (mm) | |||
| t ≤ 40 | 40 < t ≤ 80 | |||
| Límite elástico, fy | Resistencia a tracción, fu | Límite elástico, fy | Resistencia a tracción, fu | |
| S 275 N/NL | 275 | 370 < fu < 510 | 255 | 370 < fu < 510 |
| S 355 N/NL | 355 | 470 < fu < 630 | 335 | 470 < fu < 630 |
| S 420 N/NL | 420 | 520 < fu < 680 | 390 | 520 < fu < 680 |
| S 460 N/NL | 460 | 540 < fu < 720 | 430 | 540 < fu < 720 |
• Aceros soldables de grano fino, laminados termomecánicamente:
| Límite elástico mínimo y Resistencia a tracción (N/mm2) | ||||
| Tipo | Espesor nominal de la pieza, t (mm) | |||
| t ≤ 40 | 40 < t ≤ 80 | |||
| Límite elástico, fy | Resistencia a tracción, fu | Límite elástico, fy | Resistencia a tracción, fu | |
| S 275 M/ML | 275 | 370 < fu < 530 | 255 | 360 < fu < 520 |
| S 355 M/ML | 355 | 470 < fu < 630 | 335 | 450 < fu < 610 |
| S 420 M/ML | 420 | 520 < fu < 680 | 390 | 500 < fu < 660 |
| S 460 M/ML | 460 | 540 < fu < 720 | 430 | 530 < fu < 710 |
• Aceros con resistencia mejorada a la corrosión atmosférica:
| Límite elástico mínimo y Resistencia a tracción (N/mm2) | ||||
| Tipo | Espesor nominal de la pieza, t (mm) | |||
| t ≤ 40 | 40 < t ≤ 80 | |||
| Límite elástico, fy | Resistencia a tracción, fu | Límite elástico, fy | Resistencia a tracción, fu | |
| S 235 J0W | 235 | 360 < fu < 510 | 215 | 360 < fu < 510 |
| S 235 J2W | 235 | 360 < fu < 510 | 215 | 360 < fu < 510 |
| S 355 J0W | 355 | 490 < fu < 680 | 335 | 470 < fu < 630 |
| S 355 J2W | 355 | 490 < fu < 680 | 335 | 470 < fu < 630 |
| S 355 K2W | 355 | 490 < fu < 680 | 335 | 470 < fu < 630 |
• Aceros de alto límite elástico, en la condición de templado y revenido:
| Límite elástico mínimo y Resistencia a tracción (N/mm2) | ||||
| Tipo | Espesor nominal de la pieza, t (mm) | |||
| t ≤ 40 | 40 < t ≤ 80 | |||
| Límite elástico, fy | Resistencia a tracción, fu | Límite elástico, fy | Resistencia a tracción, fu | |
| S 460 Q | 460 | 550 < fu < 720 | 440 | 550 < fu < 720 |
| S 460 QL | ||||
| S 460 QL1 | ||||
4- Módulo de elasticidad longitudinal o Módulo de Young
Para comprender el concepto de Módulo de Elasticidad longitudinal del material, se debe partir del ensayo de tracción ya descrito en el apartado 2 de este tutorial. De esta manera se vio que si sobre una probeta cilíndrica de acero de sección transversal A y longitud inicial L0 se le someta a una tracción F que actúa a lo largo de su eje, ésta sufrirá, por efecto de la solicitación, un alargamiento de magnitud ΔL.
Para los estadios iniciales donde la deformación es pequeña, ΔL/L0 <<1, se obtiene experimentalmente que hasta que la fuerza aplicada F no alcance un rango limitado, éste incremento ΔL de la probeta es proporcional a la fuerza aplicada (F), a su longitud original (L0) e inversamente proporcional al área de su sección transversal (A), es decir que:
| ΔL es proporcional a | F · L0 |
| A |
A esta constante de proporcionalidad, o más bien a su inversa, se designan con las letras E, o también con Y, y se les denomina Módulo de Young o Módulo de Elasticidad longitudinal, y es una propiedad intrínseca de cada material.
Sustituyendo en la expresión anterior, ésta quedaría como sigue:
| ΔL = | 1 | · | F · L0 |
| E | A |
Por otro lado, el cociente F/A representa el nivel tensional o la tensión normal de la pieza σ, y el cociente ΔL/L0 es la deformación unitaria, ε, con lo que la expresión anterior también puede escribirse de la forma siguiente,
σ = E · ε
que es la expresión conocida como Ley de Hooke.
El Módulo de Elasticidad o Módulo de Young, para el cálculo y diseño de estructuras de acero en el rango elástico, toma convencionalmente el siguiente valor:
E= 210.000 N/mm2
A continuación, en la tabla siguiente se indica el Módulo de Elasticidad o Módulo de Young para otros distintos metales,
Metal |
Módulo de Young, Y·1010 N/m2 |
Cobre estirado en frío |
12,7 |
Cobre, fundición |
8,2 |
Cobre laminado |
10,8 |
Aluminio |
6,3-7,0 |
Acero al carbono |
19,5-20,5 |
Acero aleado |
20,6 |
Acero, fundición |
17,0 |
Cinc laminado |
8,2 |
Latón estirado en frío |
8,9-9,7 |
Latón naval laminado |
9,8 |
Bronce de aluminio |
10,3 |
Titanio |
11,6 |
Níquel |
20,4 |
Plata |
8,27 |
5- Módulo de elasticidad transversal
El módulo de elasticidad transversal, módulo de cortante o módulo de cizalla G, para la mayoría de los materiales, y en concreto para los materiales isótropos, guarda una relación fija con el módulo de elasticidad longitudinal y el coeficiente de Poisson, según la siguiente expresión:
| G = | E |
| 2 · ( 1 + ν ) |
En la siguiente tabla se indica los valores para el Módulo de elasticidad transversal, G, para distintos materiales:
Material |
G (MPa) |
Acero |
81.000 |
Aluminio |
26.300 |
Bronce |
41.000 |
Cobre |
42.500 |
Fundición Gris (4.5 %C) |
41.000 |
Hierro Colado |
< 65.000 |
Hierro Forjado |
73.000 |
Latón |
39.200 |
Decir tiene que los valores arriba indicados para los Módulos de Elasticidad, E y G, son valores constantes e iguales a los ya señalados, pero siempre y cuando nos encontremos trabajando dentro del rango de comportamiento elástico del acero.
6- Coeficiente de Poisson
El coeficiente de Poisson corresponde a la razón entre la elongación longitudinal y a la deformación transversal en el ensayo de tracción. Alternativamente el coeficiente de Poisson puede calcularse a partir de los módulos de elasticidad longitudinal y transversal, según la expresión siguiente:
| ν = | E | - |
| 1 | ||
| 2 · G |
Para el acero, toma el siguiente valor:
ν = 0,3
Como en el caso anterior, las expresiones arriba indicadas del coeficiente de Poisson, ν, son valores constantes siempre dentro del rango de comportamiento elástico del acero.
7- Estricción
Para explicar el concepto de estricción en el acero, se debe acudir de nuevo al ensayo de tracción sobre la probeta cilíndrica normalizada. Así, se conoce como período de estricción al que se inicia cuando, una vez se supera el límite de fluencia, se produce una reducción gradual de la sección en la zona donde ocurrirá la rotura, una deformación permanente, hasta que se produce definitivamente el fallo. Es por tanto, un fenómeno que ocurre durante la plasticidad del acero, y sobretodo típico de los aceros suaves o dúctiles.
La estricción es la responsable del tramo de bajada en la curva tensión-deformación, y hace que se llegue a la rotura cuando la carga es inferior a la carga máxima aplicada, diferencia que se acrecienta con la tenacidad del material.
8- Resiliencia
Mediante la Resiliencia se mide el grado de tenacidad o de ductilidad del acero a una determinada temperatura (generalmente, se establecen valores de resiliencia a temperatura ambiente, a 0ºC, o a temperatura de -20ºC).
El ensayo que proporciona el dato de la resiliencia del acero consiste en el ensayo de flexión por choque sobre una probeta Charpa, que es una probeta entallada de medidas normalizadas según la UNE 7475-1:1992. Mediante dicho ensayo, la resiliencia, medida en julios (J), se determina a una temperatura prefijada. Frecuentemente, las normas de producto exigen que las probetas absorban una energía de impacto mayor que 27 J a una temperatura de ensayo prefijada. A dicha temperatura se le denomina entonces T27J.
De tal forma, los aceros se suelen designar identificando su tipo mediante la siguiente nomenclatura que hace referencia a su límite elástico y grado (referencia a la resiliencia), según el formato siguiente:
S YYY XX,
donde,
YYY indica el límite elástico (en N/mm2)
XX indica las especificaciones de resiliencia de los distintos grados de acero de acuerdo a la siguiente tabla:
| Grado | Temperatura de ensayo (ºC) | Resiliencia (J) | ||
| t ≤ 150 | 150 < t ≤ 250 | 250 < t ≤ 400 | ||
| JR | 20 | 27 | 27 | - |
| J0 | 0 | 27 | 27 | - |
| J2 | -20 | 27 | 27 | 27 |
| K2 | -20 | 40 | 33 | 33 |
siendo t, el espesor nominal de la pieza en mm.
Ejemplo de denominación de acero según el criterio anterior es el S 275 JR.
9- Tenacidad a la fractura
La tenacidad a la fractura del acero define su capacidad a soportar cualquier solicitación exterior sin que se origine ningún tipo de fractura en el interior del material. Este es un concepto aparte de la tensión de rotura del material, y ello es así porque, en ocasiones, la fractura se puede producir con la aplicación de esfuerzos menores que los que marquen la tensión de rotura del material, o incluso menores que su límite elástico. Y ello es debido porque interiormente el material puede contener pequeñas grietas o defectos que son el germen del inicio de la fractura.
En efecto, supongamos una pieza sección A0 sometida a un esfuerzo F. El valor de la tensión normal media en cualquier sección perpendicular al esfuerzo sería σ = F/A0. Pues bien, si la pieza presenta una pequeña grieta o defecto, como puedan ser inclusiones de elementos extraños, ocurre entonces que alrededor de esta discontinuidad se produce un efecto amplifcador, un aumento del nivel de tensiones normal a que estaría sometida la pieza.
Para calibrar cuánto se amplifica los niveles de tensiones alrededor de una grieta o discontinuidad se define el Factor de Intensidad de Tensiones, K, mediante la siguiente expresión general:
K = f · σ · √ ( π · a )
donde:
f = coeficiente adimensional o factor geométrico, que depende de la fuerza aplicada y la geometría de la pieza;
σ = es el valor de la tensión normal aplicada;
a = es el tamaño del defecto. Si el defecto es superficial representa la longitud total de la grieta, mientras que si la grieta es interior, representa la mitad de su longitud.
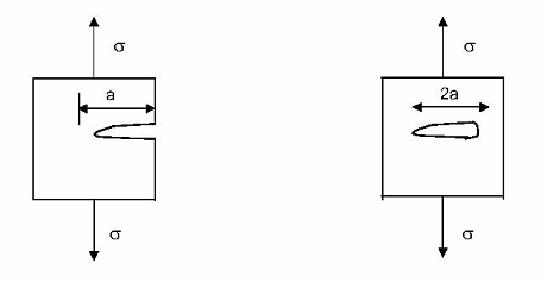
Se denomina Tenacidad a la Fractura o intensidad del esfuerzo crítico, Kc, al valor de K requerido que origina el proceso de fractura en el interior del material, comenzando en el extremo de la grieta y propagándose hasta alcanzar la superficie de la pieza ocasionando su fractura. Es decir, que la fractura ocurre cuando K > Kc. El valor numérico de Kc dependerá del espesor de la pieza considerada.
10- Dureza Brinell
La dureza es una propiedad que mide la capacidad de resistencia que ofrecen los materiales a procesos de abrasión, desgaste, penetración o de rallado. Para medir la dureza de un material se emplea un tipo de ensayo consistente en calibrar la resistencia de un material a la penetración de un punzón o una cuchilla que se usa como indentador. Este indentador usualmente consta en su extremo, o bien de una esfera, o bien de una pieza en forma de pirámide, o en forma de cono y que está compuesto de un material mucho más duro que el acero que se está midiendo. La profundidad de la entalla que produce en el acero al ser rallado por este penetrador nos dará una medida de la dureza del material.
Existen varios métodos para calibrar la dureza de un material, siendo el método Brinell y el método Rockwell los más comunes.
El método Brinell (ASTM E10) es un tipo de ensayo utilizado para calcular la dureza de los materiales. Consiste en una esfera de 10 mm de diámetro, usualmente de un acero endurecido, que se presiona contra la superficie del material objeto de estudio bajo una carga estática de 3.000 kg. El tamaño de la huella nos proporcionará una medida de la dureza, denominada dureza Brinell, bajo estas condiciones del ensayo.
Para determinar el valor de la dureza Brinell se emplea la ecuación mostrada en la figura siguiente:
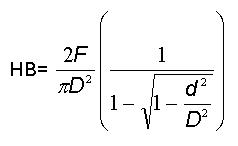
donde:
F, es la carga a utilizar, en Kp
D, es el diámetro de la bola (indentador), en mm
d, es el diámetro de la huella dejada en superficie, en mm
A continuación, en la siguiente tabla se indica, entre otras propiedades mecánicas, los valores de dureza para distintos tipos de acero:

11- Soldabilidad
La soldabilidad mide la capacidad de un acero que tiene a ser soldado, y que va a depender tanto de las características del metal base, como del material de aporte empleado.
Un parámetro útil para evaluar la soldabilidad de los aceros es el concepto de CARBONO EQUIVALENTE (CEV), que equipara las soldabilidades relativas de diferentes aleaciones de acero y las compara con las propiedades de un acero al carbono simple.
El Código API 1104- A B presenta la ecuación desarrollada por el Instituto Internacional de Soldadura, y cuya expresión es la siguiente, donde los contenidos de los elementos químicos se expresan en tanto por ciento (%):
| CEV = C + | Mn | + | Cr + Mo + V | + | Ni + Cu |
| 6 | 5 | 15 |
A medida que se eleva el contenido equivalente de carbono, la soldabilidad de la aleación de acero que se trate decrece.
Aunque esta ecuación fue inicialmente desarrollada para caracterizar la tendencia a la fisuración por hidrógeno en chapas de acero, también se ha venido utilizando para evaluar el endurecimiento del acero basado en su composición química.
Como regla general, un acero se considera soldable si el carbono equivalente, obtenido según la fórmula anterior, es menor a 0,4%.
No obstante, este parámetro no es suficiente para evaluar la soldabilidad de los distintos aceros, dado que la soldabilidad no depende sólo de la composición química del acero, sino que existen otros factores como puede ser el espesor de la junta, un factor que va a condicionar la elección de la temperatura de precalentamiento y/o tratamientos térmicos post-soldadura, o la adecuada elección del material de aporte. Otros aspectos como la historia térmica del material y tensiones mecánicas desarrolladas antes, durante y después de realizada la unión, van a influir también en la soldabilidad del acero.
Diagrama de Graville
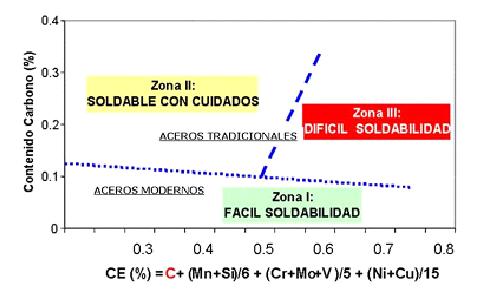
La figura anterior muestra el diagrama de Graville, el cual resulta una herramienta útil para evaluar la soldabilidad de los aceros. El valor del CE (%), como ya se ha dicho, va a medir la susceptibilidad a la fisuración en frío del metal base en la zona afectada por el calor (ZAC) debido a la soldadura. Como se vio, mayores %C va a significar un aumento del riesgo que se produzca una fisuración en frío.
Otra información a extraer del diagrama de Graville es la posibilidad de comprobar la necesidad de tener que realizar algún tipo de precalentamiento o tratamiento térmico post-soldadura basada en la composición química (no considera espesor), dado que en la misma gráfica se indica la relación entre %Carbono y el CE% del metal base.
En función en qué zona se encuentre el metal base objeto de soldadura, se pueden considerar tres zonas distintas, a saber:
- Zona I: Aceros de bajo carbono y bajo endurecimiento no susceptibles a fisuras, y por lo tanto de fácil soldabilidad.
- Zona II: Aceros con mayor porcentaje de carbono y bajo endurecimiento. En esta zona el riesgo a fisuras en la ZAC es mayor, pero en parte puede ser evitado mediante el control de la velocidad de enfriamiento, gracias a que se realice un aporte térmico después de realizada la soldadura, o bien, se realice un precalentamiento previo más ligero.
- Zona III: Es la zona de más difícil soldabilidad. La ocupa los aceros con elevado porcentaje de carbono y alto endurecimiento, lo que origina la formación de microestructuras susceptibles a fisuras.
Desde el punto de vista de selección de parámetros de soldadura este diagrama indicaría que si por su composición química un acero se ubica en la Zona II, entonces implicaría que su soldadura debe involucrar el uso de procesos de bajo hidrogeno y precalentamiento, mientras que si un acero es ubicado en la Zona III se deben aplicar procesos de bajo hidrógeno, precalentamiento y tratamientos térmicos post-soldadura, todo ello con el fin de mejorar la calidad final del cordón de soldadura realizado.
12- Resistencia al desgarro
La resistencia al desgarro laminar del acero se define como la resistencia a la aparición de fisuras en piezas soldadas sometidas a tensiones de tracción en dirección perpendicular a su superficie.
Para evitar el desgarro laminar, se deberá reducir en lo posible dichas tensiones mediante un proyecto adecuado de los detalles constructivos correspondientes.
También se puede emplear otros tipos aceros que son poco susceptibles a este defecto, tales como los aceros con resistencia mejorada a la deformación en la dirección perpendicular a la superficie del producto, y que son aquellos que cumplen con unos valores mínimos de estricción mostrados en la siguiente tabla, y que han sido obtenidos sometiendo al producto a un ensayo de tracción en la dirección del espesor.
Tabla de Grados y Valores mínimos de estricción
| Grado | Estricción (%) | |
| Valor mínimo medio de tres ensayos | Valor mínimo individual | |
| Z 15 | 15 | 10 |
| Z 25 | 25 | 15 |
| Z 35 | 35 | 25 |
13- Aptitud al doblado
La aptitud al doblado es un índice de la ductilidad del material, y se define por la ausencia o presencia de fisuras en el ensayo de doblado. La aptitud al doblado es una característica opcional que debe verificarse sólo si lo exige el pliego de prescripciones técnicas particulares del proyecto o si lo indica el pedido.
La determinación de la aptitud al doblado se efectuará comprobando la ausencia de fisuras en el ensayo de doblado simple, normalizado en UNE-EN ISO 7438.
14- Otros datos de diseño
Para el diseño de estructuras de acero se toman, para las características siguientes, los valores que a continuación se indican:
• Punto de fusión:
El punto de fusión depende del tipo de aleación que se trate y de las concentraciones de los distintos elementos aleantes. El punto de fusión del hierro puro es de 1.510 ºC, sin embargo el del acero está entorno a los 1.400 ºC, aunque esta temperatura varía con el contenido de carbono en la siguiente manera:
- Acero de bajo carbono: 1.510 ºC
- Acero de medio carbono: 1.430 ºC
- Acero de alto carbono: 1.370 ºC
• Punto de ebullición: 2.500 ºC
• Calor específico: 0,11 Kcal / Kg ºC
• Coeficiente de dilatación lineal: α = 1,2 · 10-5 ºC-1
• Densidad: γ = 7.850 Kg/m3
ANEXOS
Anexo 1.- Diagrama Hierro-Carbono (Fe-C)
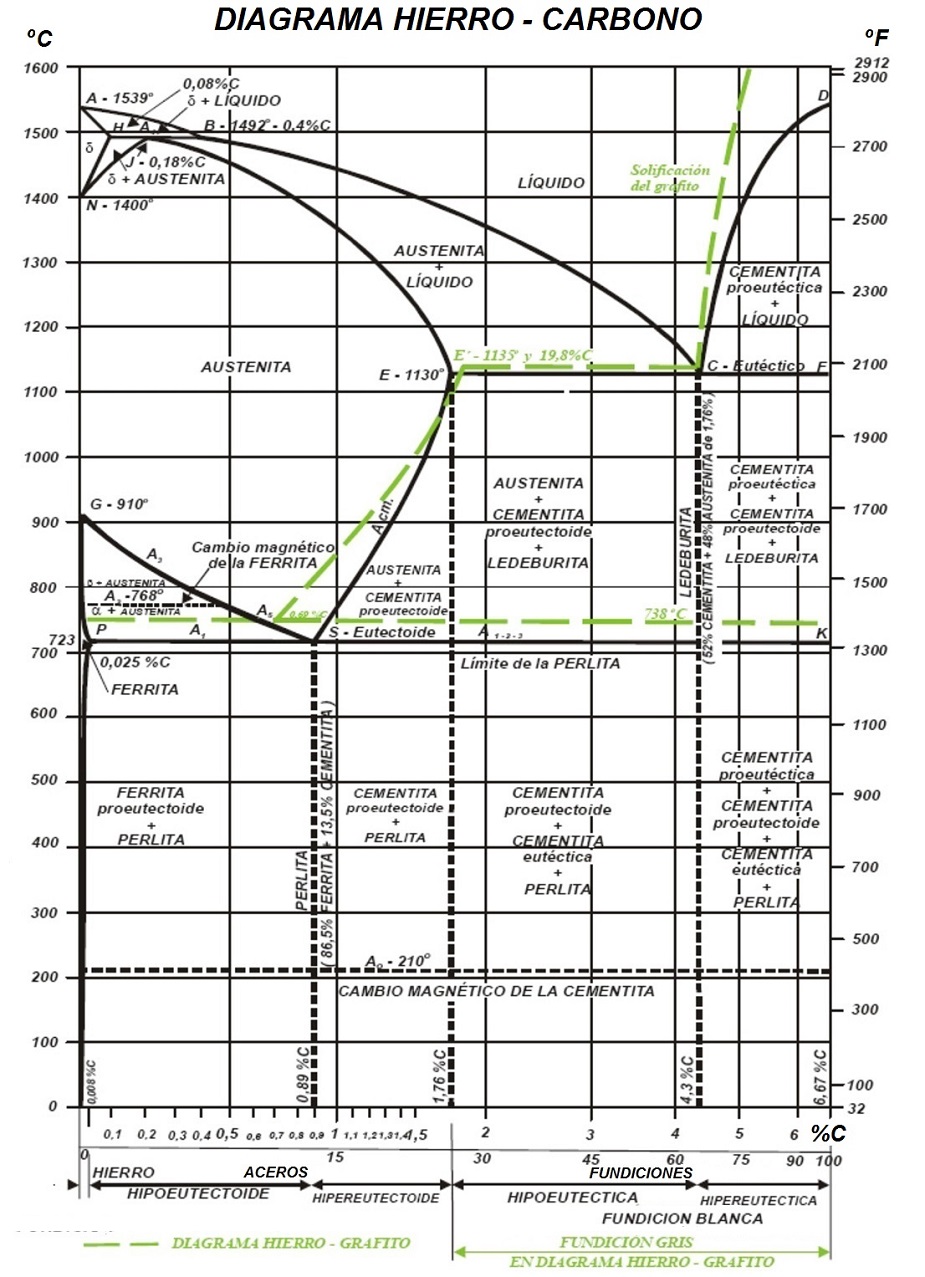
Anexo 2.- Propiedades mecánicas de aceros estructurales según norma europea EN
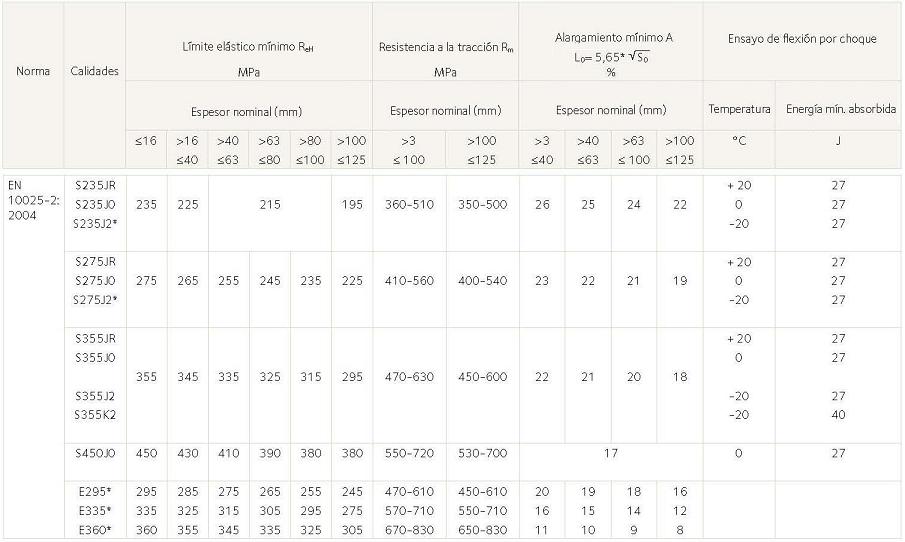
Anexo 3.- Composición química de aceros estructurales según norma europea EN
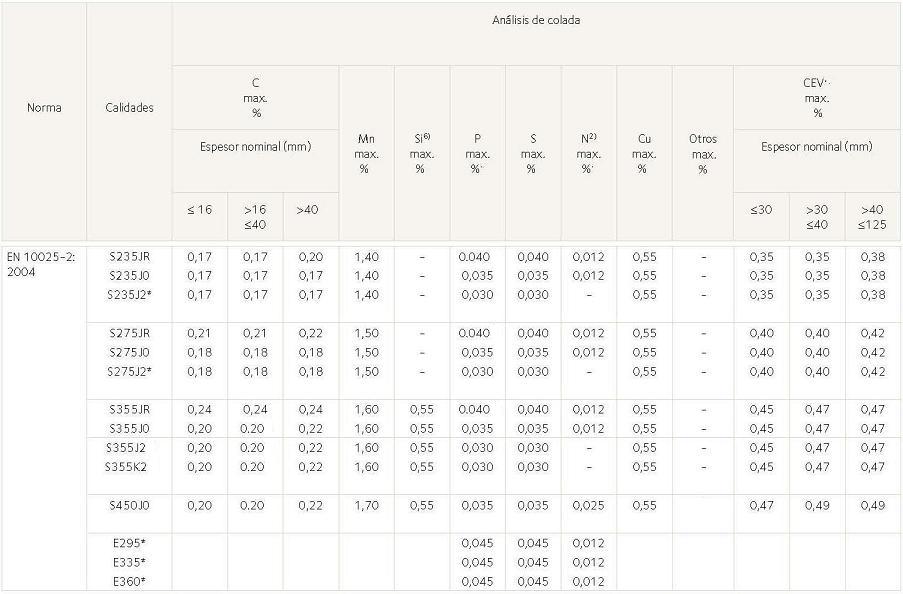
Anexo 4.- Propiedades mecánicas de aceros estructurales según norma americana
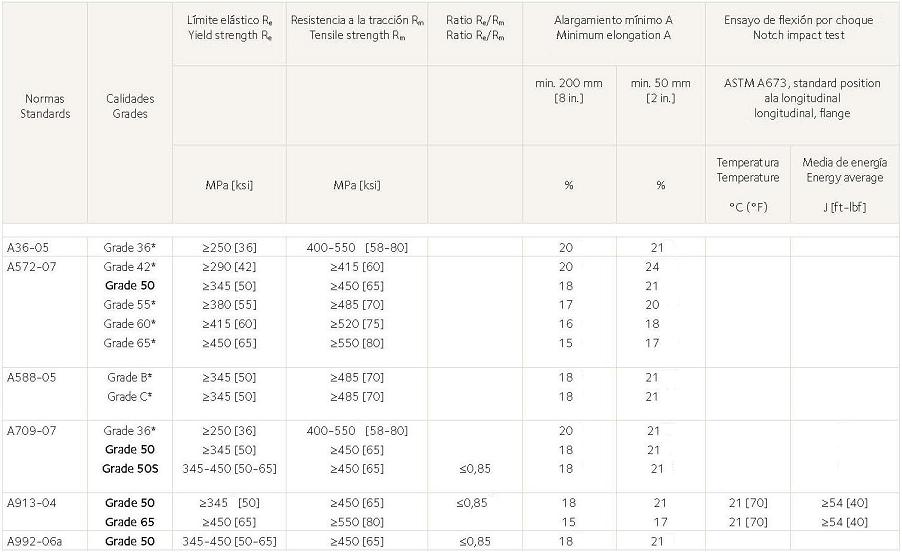
Anexo 5.- Composición química de aceros estructurales según norma americana
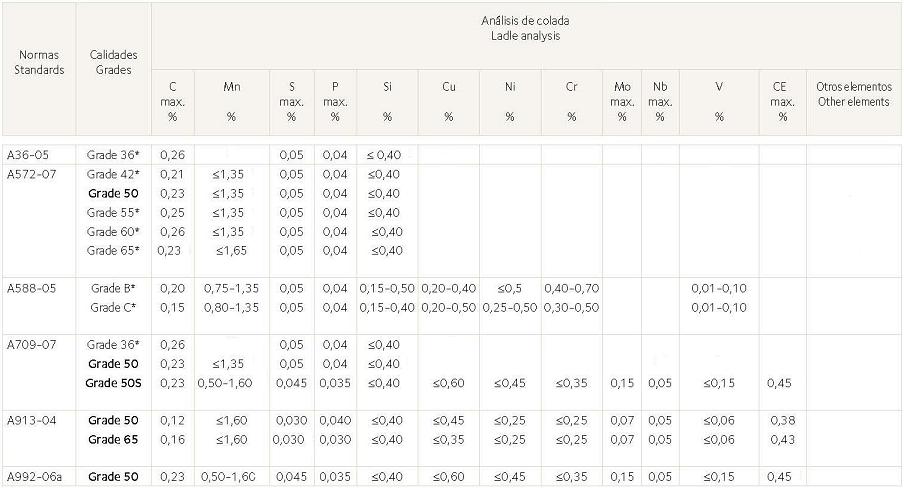
>> FIN DEL TUTORIAL
Programa de Colaboración
Ahora puedes colaborar en el sostenimiento de esta web realizando un pequeño donativo
Gracias por tu colaboración
Hermenegildo Rodríguez Galbarro
Editor y Responsable de esta Web. [+info]
Información y consulta:
Hermenegildo Rodríguez Galbarro
info@ingemecanica.com - Tel. 646 166 055


